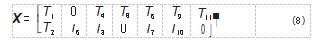SCI论文(www.lunwensci.com)
摘要 :舰船是一个复杂装备, 其维修任务中所涉及的维修工具种类繁多, 涉及的维修零部件结构复杂, 维修过程需要多个维修人 员执行, 若没有进行合理的维修任务分配, 将会造成维修现场无序和混乱的现象, 进而影响舰船维修任务进程 。针对上述问题, 根据实际舰船维修任务分配, 以不同任务之间的约束关系, 建立问题描述的数学模型 。考虑到粒子群算法容易陷入局部最优的问 题, 以粒子群算法为基础, 引入遗传算法的交叉和变异操作, 用遗传算法的全局搜索能力来避免陷入局部最优问题, 用粒子群算 法快速收敛的特性提高遗传算法的收敛速度, 从而对粒子群算法进行改进 。以某舰船传动装置维修为例进行了 15 次测试实验, 结 果表明, 改进粒子群算法平均最优适应度为 61.78. 相较于粒子群算法的 63.23. 改进粒子群算法能够获得更优的计算结果 。提出 的方法在解决维修任务分配问题方面更加合理有效。
关键词 :舰船维修,任务分配,多人协同,粒子群算法
Research on Task Assignment of Ship Maintenance with Multi-person Cooperation
Du Du1. Li Yang2. Li Fangzheng1. Yi Pengxing2. Huang Junjie2
( 1. Unit 92578 of PLA, Beijing 100161. China;
2. School of Mechanical Science and Engineering, Huazhong University of Science and Technology, Wuhan 430074. China) Abstract: Ship is complex equipment, and its maintenance tasks involve a wide variety of maintenance tools and complex structures of maintenance components. The maintenance process requires multiple maintenance personnel to execute . If there is no reasonable allocation of maintenance tasks, it will cause disorder and chaos in the maintenance site, thereby affecting the progress of ship maintenance tasks. Aiming at the above problems, according to the actual ship maintenance task assignment problem, the mathematical model of problem description is established based on the constraint relationship among different tasks . Considering that the particle swarm algorithm easy to fall into local optimum problem, based on particle swarm optimization algorithm and introduce the crossover and mutation operators of genetic algorithm , using the global search ability of genetic algorithm to avoid falling into local optimum problem , with fast convergence characteristics of particle swarm optimization algorithm to improve the convergence speed of genetic algorithm ,thus to improve the particle swarm algorithm. Taking the maintenance of a warship transmission as an example, 15 test experiments are carried out. The results show that the average optimal fitness of the improved particle swarm optimization algorithm is 61.78.which is better than the 63.23 of the particle swarm optimization algorithm . The proposed method is more reasonable and effective in solving the problem of maintenance task allocation .
Key words: ship maintenance; task allocation; multi-person collaboration; particle swarm optimization algorithm
引言:舰船装备维修任务涉及到的维修零件 、维修工具 、 维修对象等维修资源种类繁多且过程复杂, 缺少统一的 模型表达, 国内外相关学者在这方面也做了较多的研究。 在舰船维修任务分配方面, 协同维修任务分配主要研究 根据既定维修目标, 合理分配维修任务实现多人并行作 业, 被应用于多无人机协同作战 、多水下机器人协同探 测以及救援机器人协作[ 1-2]等领域。
白璐[3] 将核设施场景中设备拆除 、场址清污等作业 任务的分配问题进行抽象和简化, 通过讨论任务需求人 员数目和待分配人员数目的数量关系, 采用匈牙利法进行了求解 。秦新立[4] 在求解多机器人任务规划问题时, 以问题复杂度为基准建立了上层机器人编队与下层机器 人站位的双层规划模型, 通过改进蚁群算法对机器人编 队任务分配进行了求解 。现有文献对协同问题的研究多 集中在任务分配的建模与启发式搜索算法优化方面, 并 将其应用到大规模机器人等任务分配中 。但在此类问题 的求解中不同任务之间的差异性并不明显, 主要体现在
执行地点及所需时间的不同, 且忽略了任务的执行过程, 即认为机器人等单元体是具有一定智能性的[5], 对其进 行指派后可自行完成所分配任务 。维修任务复杂程度较 高且干涉性较强, 对多人协同维修任务分配领域的研究相对较少, 而相近领域的研究已经证明该问题属于 NP- hard 问题, 随着问题规模的增大, 求解的难度和解的数 量均会快速增加[6-7] 。本文分析了不同元任务类型的约束 关系, 建立了多人协同维修任务分配的数学模型, 提出 了基于粒子群算法的多人协同舰船维修元任务分配方法。 以舰船某传动装置维修为例, 通过比较分析验证了改进 算法的有效性及优越性。
1 多人协同舰船维修任务分配约束关系
1.1 优先约束关系
优先约束是最为常见的约束关系, 反映了元任务之 间的先后顺序 。简单的优先约束关系仅涉及到串行形式 的元任务 。较为复杂的优先关系约束为元任务之间存在 并行关系, 只有当两种任务都完成后才能执行下一个元 任务。
对于以上元任务之间的优先约束可以用式 ( 1) 表 示:
1.2 协同约束关系
协同约束主要用于判断元任务能否分配给不同维修人员并行进行, 是多人协同维修任务分配的重点。
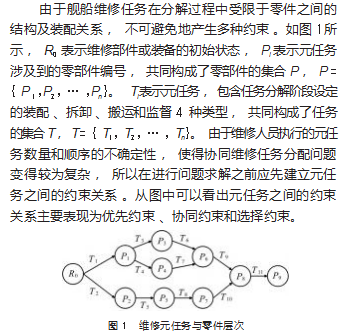
协同约束关系在元维修的同一层次等级上和不同层 次等级上均有体现, 如在同一层次等级上元任务 T3 与元 任务 T4 互不干涉, 可以同时进行, 这两个元任务具有协 同关系 。在不同等级上, 元任务 T1 与元任务 T5 、T8 之间 也具有协同关系, 这几个元任务同样也可以并行执行 。 元任务的协同约束关系可以用式 ( 3) 进行表示:
1.3 一致约束关系
任务层次图的中间某个环节存在多个元任务同时指 向同一零部件的情况, 如图 1 中的 T6 、T7 及 T9 、T10 。这 种约束的出现是由于在维修任务的某一阶段会对同一零 部件执行相同的维修元任务 。若将具有此种约束关系的 元任务分配给单个维修人员, 该维修人员执行这些元任 务的总时间应为单个元任务的所需时间, 若分配给多个 维修人员, 这些元任务执行时的起始时间应当是一致的。 所以要对这种一致约束关系进行限定, 反映在维修任务 序列中 。一致约束关系可表示为:
2 多人协同舰船维修任务分配数学模型
2.1 编码方式
由于协同任务分配问题涉及到元任务和维修人员 的对应关系, 这里结合拆卸序列规划[8-9] 、任务人员匹 配调度[8] 等问题的研究, 采用实数编码的方式对多人 协同舰船维修任务分配问题进行描述, 其编码空间与 解空间可以保持一致, 求得的编码序列即为该问题的 解[10-11]。
这里, 矩阵行数为协同人数, 矩阵中的行元素表示 某一维修人员所需执行元任务序列集合 。矩阵列数表示 单个维修人员执行的最大元任务数, 若其分配到的元任 务数量少于单人最大元任务数 k, 则将此行缺省值设为 0. 这样即可对多人协同维修任务分配方案进行合理表 示 。以图 1所示的任务序列为例, 若并行度为 2. 单个维修人员执行的最大元任务数为 7 的并行任务顺序为: X = (T1 , T2 → T5 → T3 , T4 → T8 → T6 , T7 → T9 , T10 → T11 ), 可用矩阵表示为:
这样就完成了从单人串行元任务序列到多人并行元 任务序列的转变。
2.2 目标函数
对于舰船装备的维修任务, 在维修资源给定的情况下, 不同的维修任务分配方案主要造成维修时间的不同。 因此将维修时间作为多人协同维修任务分配方案的目标 函数。
假设不同维修人员的维修能力都是相同的, 即由不 同维修人员执行相同元任务时所需时间相同 。对于多人 协同维修, 每个维修人员都有相应的元任务执行序列, 同时会有与其对应的维修时间 。单个维修人员执行元任 务所需总时间可表示为:
式中: Th 为第 h 个维修人员执行分配到自身的元任务所 需总时间; ti 为执行第 i 个元任务所消耗的时间; yih为时 间协同系数, 该系数的存在使得相同元任务可以由多个 维修人员共同执行, 其数值根据不同元任务类型来设定。
对元任务进行分配时, 一旦确定其执行方式, 在执 行过程中不能再改变, 即其他维修人员不能在该元任务 执行过程中加入或离开。
对于不同的维修任务分配方案, 各维修人员会有与 之对应的维修时间, 则维修任务所需总维修时间可用式 ( 10) 表示:
3 基于改进粒子群算法的维修任务分配
粒子群算法是基于鸟群觅食过程行为机制, 从初始 解出发, 通过迭代不断寻找最优解的智能搜索算法[12]。 经典的粒子群算法虽然可以通过对个体和全局的极值进 行寻优完成搜索过程, 但随着后期迭代次数的增加, 种 群中的粒子相似度会不断提高, 容易陷入局部最优[13-14]。 因此考虑以粒子群算法为基础, 引入遗传算法的交叉和 变异操作, 用遗传算法的全局搜索能力来使粒子群搜索 避免陷入局部最优, 同时结合粒子群算法快速收敛的特 性提高遗传算法的收敛速度。
在一个 D 维搜索空间中, 设粒子群由 N 个粒子组成, 则可将其中一个粒子表示为 D 维向量。
本文结合遗传算法中的交叉和变异操作, 通过引入 交叉算子和变异算子实现对粒子自身速度和位置的更新。交叉时有多种交叉 方式, 以单点随机交叉 为例对更新方式进行说 明 。交叉时首先随机确 定要交叉的点, 当两个 体交叉完成后需要比较 更新后的个体适应度值, 若交叉后的个体适应度 值大于原适应度值, 则 进行替换; 否则, 不进 行替换 。此种交叉方式 可以避免种群由于交叉 的随机性而丢失优秀的 个体 。变异的操作采用 正态变异, 即先随机产 生 一 个 变 异 的 基 因 点, 然后产生一个服从正态分布的随机数, 用此随机数去替换原来基因片段中该点 的编码值, 同时也对适应度进行比较并决定取舍 。在实 际问题求解过程中, 变异概率的值一般较小, 因此也不 会引起优秀个体的丢失。
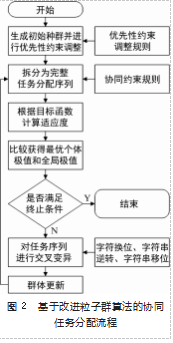
改进后的整体算法流程图如图 2 所示。
4 舰船装备维修实例应用
4.1 实例求解
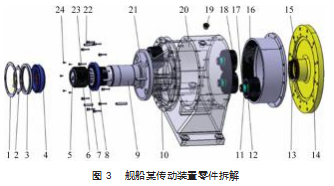
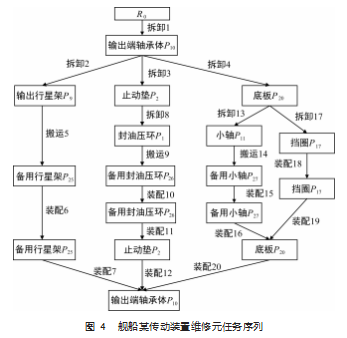
这里以某舰船传动装置维修为例进行说明, 主要维 修任务为更换损坏行星架 、封油压环和小轴并检查挡圈, 使用 MATLAB R2017a 软件编写求解算法 。图 3 为该装备 的零件拆解图, 共包含 24 个拆卸单元, 维修元任务序列 如图 4 所示。
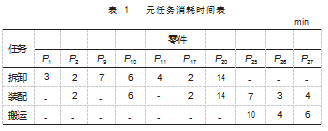
元任务后面的数字表示该任务的编号, 共有 20 个元 任务, 箭头指向元任务对应的零件, R0 表示系统初始的 维修状态 。在对不同维修任务进行分配前应确定各维修 任务所需要的维修时间, 不同元任务的时间消耗如表 1 所示。
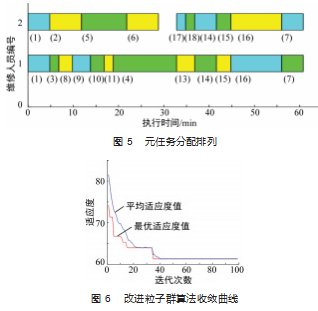
考虑到舰船维修任务的复杂程度, 选取 2 名维修人 员对传动装置维修进行协同作业 。 同时, 设置改进粒子群算法主要参数为: 种群数 50. 最大迭代次数 100. 字 符换位概率为 0.8. 字符串逆转概率 0.8. 字符串移位概 率为 0.8. 变异概率为 0.05. 经过反复迭代获得最优任务分配序列为: 1→ 3→ 8→9→ 10→ 11→4→ 13→ 14→ 15→ 16 →7 和 1→2→5→6→ 17→ 18→ 14→ 15→ 16→7. 最佳适应 度值 60.8. 元任务分配结果如图 5 所示, 算法收敛曲线 如图 6 所示, 首次出现最优解是在第 35 代。
4.2 结果分析与比较
( 1 ) 对比分析 1
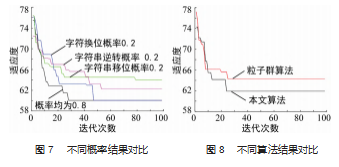
因本文改进算法中采用遗传算法的交叉变异操作对 粒子进行更新, 为了研究多人协同任务分配问题中此种 方式对算法性能的影响, 本文选择不同概率的字符换位、 字符串逆转 、字符串移位等遗传操作方式进行实验, 同 时与概率均为 0.8 的情况进行对比, 结果如图 7 所示。
从结果中可以看出, 在字符换位概率较小时, 算法 收敛速度较慢; 字符串移位和字符串逆转概率较小时, 获得的最佳适应度值要差于概率较大的情况, 难以获得 全局最优解; 字符串移位和字符串逆转是影响算法局部 搜索能力的重要参数; 3 种方式对算法的收敛速度均有 影响, 需要对其合理设置得到最优结果。
( 2) 对比分析 2
为了验证本文算法的有效性和优越性, 与粒子群算 法进行了比较, 不同算法的收敛曲线对比结果如图 8所 示 。从实验结果中可以看出, 本文算法求得的最优解要 好于粒子群算法, 同时在算法收敛速度方面, 两者均在 25代左右达到最优 。从算法原理进行分析, 本文算法因 加入遗传算法的交叉及变异更新方式提高了粒子多样性, 增强了粒子的全局搜索能力, 所以在最优值方面会有较 好的效果, 而本文算法的迭代方式与粒子群算法相似, 在收敛速度方面两者应有类似的表现 。因此, 实验结果 与理论分析相一致。
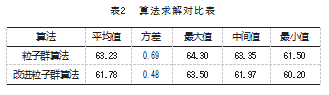
另外, 由于算法交叉变异等方式本身存在偶然性, 为了获得更为准确的实验结果, 这里对不同算法分别进 行 15次计算, 获得的平均值等数据如表 2所示 。 由结果 可以看出, 相比粒子群算法, 本文算法能够较快地收敛 且获得较优的计算结果。
5 结束语
本文深入研究了多人协同舰船维修任务分配问题, 提出了元任务之间的优先 、协同和一致三种约束关系, 同时建立了多人协同舰船维修任务分配的数学模型, 结 合可变矩阵的编码方式, 为问题求解设立了目标函数及 解的初始化方式; 然后结合粒子群算法, 对粒子更新方 式进行改进, 在算法中引入遗传算法中的交叉算子和变 异算子, 提出改进粒子群算法的多人协同舰船维修任务 分配流程; 最后, 结合舰船某动力设备进行实例求解, 研究了不同条件下的更新方式对算法性能的影响, 同时 与粒子群算法进行比较, 验证改进粒子群算法具有更改 的适应度结果, 能更好地进行维修任务分配, 对于维修 任务的高效执行具有现实意义。
参考文献:
[1] Moon S,Oh E,Shim D H. An Integral Framework of Task Assign ⁃ ment and Path Planning for Multiple Unmanned Aerial Vehicles in Dynamic Environments[J]. Journal of Intelligent & Robotic Systems,2013.70(1/2/3/4):303-313.
[2] Zhu D,Huang H,Yang S X. Dynamic Task Assignment and Path Planning of Multi-AUV System Based on an Improved Self-Or⁃ ganizing Map and Velocity Synthesis Method in Three-Dimen ⁃ sional Underwater Workspace[J]. IEEE transactions on systems, man,and cybernetics, 2012.43(2):504-514.
[3] 白璐 . 核设施场景下多人协同作业研究[D].哈尔滨:哈尔滨工 程大学,2018.
[4] 秦新立 . 多机器人协同任务分配与路径规划的研究[D]. 天津: 天津大学,2018.
[5] 李华伟 . 多无人机协同任务规划研究与实现[D]. 西安:西安电 子科技大学,2014.
[6] Lu Yingtong. Task Assignment of UAV Swarm Based on Wolf Pack Algorithm[J]. Applied Sciences,2020.10(23): 8335.
[7] 李建军 . 基于群体智能的多 AUV 协同任务分配方法研究[D]. 哈尔滨:哈尔滨工程大学,2018.
[8] Cong Lu, Ya Chao Liu. A disassembly sequence planning ap ⁃ proach with an advanced immune algorithm[J]. Proceedings of the Institution of Mechanical Engineers, Part C: Journal of Me⁃ chanical Engineering Science,2012.226(11): 2739-2749.
[9] 杨得玉,徐志刚,朱建峰,等 . 考虑产品故障特征的目标选择性 拆卸序列规划[J].哈尔滨工业大学学报,2019.51(7):160-170.
[10] 赵亚玲 ,葛茂根 ,扈静 ,等 . 柔性生产中基于人员任务匹配度 的 人员调度[J]. 合肥工业大学学报( 自然科版),2015.38(2):270-273.
[11] 昝翔,陈春良,张仕新,等 . 多约束条件下战时装备维修任务分 配方法[J].兵工学报,2017.38(8):1603-1609.
[12] 赵雪森 ,王社伟 ,邵校 . 基于改进量子粒子群优化算法的 多 UCAV 协 同 任 务 分 配 研 究 [J]. 四 川 兵 工 学 报 ,2015(10):120-124.
[13] 牛龙辉,陈海洋,季野彪 . 结合粒子群算法与任务分配协调策 略的仓储多机器人任务分配[J]. 西安工程大学学报,2020.34 (6):73-79.
[14] 王峰,张衡,韩孟臣,等 . 基于协同进化的混合变量多目标粒子 群优化算法求解无人机协同多任务分配问题[J]. 计算机学 报,2021.44(10):1967-1983.
[15] 唐必伟 . 粒子群算法的改进及其在无人机任务规划中的应 用[D]. 西安:西北工业大学,2017.
关注SCI论文创作发表,寻求SCI论文修改润色、SCI论文代发表等服务支撑,请锁定SCI论文网!
文章出自SCI论文网转载请注明出处:https://www.lunwensci.com/ligonglunwen/63852.html