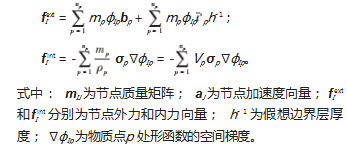SCI论文(www.lunwensci.com)
摘要:在土壤切削数值模拟研究中, 常见的有限元法会因网格扭曲变形严重而减慢甚至终止, 而离散元法存在土壤参数标定复杂 等问题。针对以上问题, 为提高土壤切削数值模拟精度, 采用数值计算方法——物质点法, 基于土壤的理想弹塑性本构关系以及 莫尔-库伦失效准则和最大主应力失效准则建立了土壤切削模型。将数值模拟结果同已发表的试验数据对比, 发现在土壤不同区域 的变形预测及其动态演化过程中, 本文数值模拟结果同试验结果高度吻合: 剪切角误差不超过 2.5°、剪切长度平均误差为 10.4mm; 在土壤发生剪切失效时, 对土壤切削阻力预测精度较高, 平均误差为 3.4%。验证了物质点法在土壤切削过程模拟的可行性与有效 性, 为土壤切削过程的数值模拟提供了新思路。
关键词:土壤切削过程,物质点法.数值模拟,土壤刀具互作模型
Numerical Simulation of Soil Cutting Process Based on Material Point Method
Zhou Aiguo, Luo Hong, Xu Xiufeng, Xu Yichao, Zhu Yutian
(School of Mechanical Engineering, Tongji University, Shanghai 201804. China)
Abstract: In the numerical simulation research of soil cutting, the commonly used finite element method (FEM) may slow down or even terminate due to severe mesh distortion, while the discrete element method (DEM) has complex soil parameter calibration problems . Aiming at the above issues, in order to improve the accuracy of soil cutting numerical simulation, a soil cutting model was established with a numerical calculation method - the material point method(MPM), based on the ideal elastic-plastic constitutive relationship of the soil, as well as the Mohr Coulomb failure criterion and maximum principal stress failure criterion . The numerical simulation results are compared with published experimental data. The results show that in the deformation prediction and dynamic evolution process of different soil regions, the numerical simulation results in this paper are highly consistent with the experimental results: the shear angle error does not exceed 2.5°, and the average shear length error is 10.4mm; When soil shear failure occurs, the prediction accuracy of soil cutting resistance is relatively high, with an average error of 3.4%. The feasibility and effectiveness of the material point method in soil cutting process simulation are verified, which provides a new idea for the numerical simulation of soil cutting process .
Key words: soil cutting process; material point method; numerical simulation; soil-tool interaction model
引言
在土壤切削过程的数值模拟研究中, 有限元法 (Fi⁃ nite Element Method, FEM) 和 离 散 元 法 (Discrete Ele⁃ ment Method, DEM) 应用最为广泛。 FEM 多被应用于土 壤变形较小的场合[1-3], 变形过大将导致有限元网格严重 扭曲, 致使计算减慢甚至终止。且在处理较大土壤变形 时需要预先指定失效面[4-5]。离散元法多用于处理无黏性 的颗粒土或岩石, 能够得到相对准确的土壤切削模型[6], 但是土壤离散元模型参数标定工作非常复杂[7]。除此之 外, 计 算 流 体 动 力 学 (Computational Fluid Dynamics , CFD) 也用于仿真土壤切削过程, 但 CFD 仅能模拟切削 类似流体的土壤, 且计算精度较低[6]。
物质点法 (Material Point Method, MPM) 由 Sulsky 在 1994 年提出, 是一个相对较新的数值计算方法, 旨在处理碰撞、侵彻等大变形问题[8]。近年来, 由于在爆炸、 高速冲击等大变形问题上的成功应用[9], MPM 受到越来 越多研究人员的关注并被应用于其他研究领域[10- 12]。但 目前未见在土壤切削过程的数值模拟研究上应用 MPM。
本文基于物质点法, 采用基于 Anura3D 软件建立土壤 切削模型,分析土壤切削参数包括切削角度、切削深度和 切削速度对剪切角、剪切长度和切削阻力等的影响。通过 仿真结果与试验数据对比验证其可行性与有效性, 以期能为 土壤切削过程研究提供新思路并扩展物质点法的应用领域。
1 物质点法理论
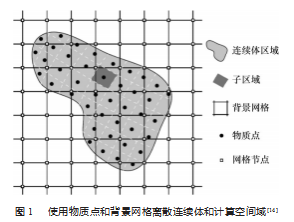
物质点法的基本思想是将连续体离散成一系列物质 点, 物质点代表其所在位置的子区域, 携带和存储了该 区域的物理信息, 而控制方程的计算是通过背景网格来 完成的[9. 13], 如图 1 所示
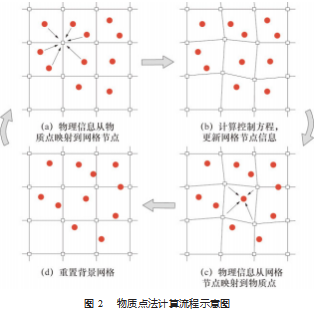
物质点和背景网格节点之间的连接桥梁是形函数。 在计算控制方程之前, 通过形函数将物质点信息映射到 网格节点, 在网格节点上计算控制方程并更新物理信息, 之后再将物理信息通过形函数映射回物质点, 最后重置 背景网格, 完成一个时间步的计算, 如图 2 所示。由于 在每个时间步的开始前背景网格会被重置, 因此网格变 形不会累积, 从而能够克服有限元法网格变形持续累积 造成的网格畸变, 时间步长急剧减小等缺点, 因而可以 运用到大变形的仿真计算中。
1.1 运动方程
初始阶段划分好物质点离散之后, 所有物质点的质 量在整个计算过程中不再改变, 因而算法自动满足质量 守恒。角动量守恒使得柯西应力张量 σ 为对称张量[13]。在土壤切削过程中一般不涉及热效应,可以不考虑能量守 恒控制方程。因此最终需要考虑线动量守恒方程 (也即运 动方程)、初始条件和边界条件。运动方程微分形式如下:
1.2 形函数
在物质点和背景网格节点之间进行物理信息映射的 过程中, 形函数起到重要作用。映射关系可以通过以下 公式表达。
通过对式 (6) 进行求解, 可以求得所有网格节点的 加速度, 进而可以更新其他物理量, 之后通过式 (3) 将 信息映射回物质点, 至此便完成了一个时间步内的所有 计算。根据时间步长, 以同样方式循环计算每一个时间 步, 便能得到动态结果。
2 数值计算模型
Anura3D[15] 软件是一款使用物质点法专门用于对大 变形和土壤-水-结构相互作用等问题进行数值建模和研 究的软件, 其在处理土壤大变形问题上的可行性上已被 证实[12. 16]。本文采用 Anura3D[15]软件进行数值模拟。
基于文献[17 – 19]的试验数据, 针对黏性土壤建立 相同条件的物质点法模型, 并将数值模拟结果和试验结 果对比来验证物质点法在土壤切削研究中的可行性。
2.1 土壤模型
土壤采用理想弹塑性本构模型, 对于剪切失效, 采 用莫尔-库伦准则, 对于拉伸失效, 采用最大主应力准 则, 模型参数可通过常规三轴压缩和拉伸试验获得。理 想弹塑性本构模型在相同围压下的单轴压缩的偏应力 σ d-轴向应变 εx 曲线如图 3 (a) 所示。莫尔-库伦准则和 最大主应力准则相结合的失效准则的广义剪应力 q-平均 应力p 曲线如图3 (b) 所示, 其屈服面方程分别为
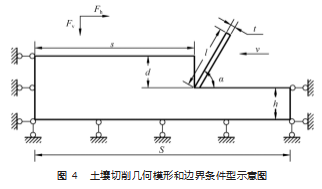
2.2 几何模型和边界条件
数值模拟几何模型和边界条件如图 4 所示。为模拟 试验条件, 对土壤前后方施加水平约束, 对土壤底部施
3 数值模拟结果与分析
为便于分析和减少仿真模拟次数, 以 α = 60°, d = 100 mm, v = 100 mm/s 试验条件作为基准组或对照组。 为研究切削参数对土壤切削过程的影响, 以基准组为参 考, 针对切削角度设定了 30°, 45°, 75° 和 90° 试验组, 针对切削深度设定了 50 mm 和 150 mm 试验组, 针对切削 速度设定了 100 mm/s 和 140 mm/s 试验组, 因此一共进行 了 9 组仿真试验。
3.1 网格密度确定
同有限元一样, 物质点法也存在收敛性问题, 即网 格密度会显著影响仿真计算的结果, 只有当网格密度足 够大时, 其结果才能逼近真实解。为找到适合的网格密 度, 在基准条件下, 设定单元长度分别为 10、8、6 mm (由于采用三角形单元, 实际网格中单元边长最小长度约 为设定长度的 0.7倍), 设定每个单元中物质点数量为 3. 6 mm 单元组初始网格划分如图 5 所示。
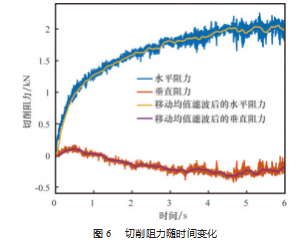
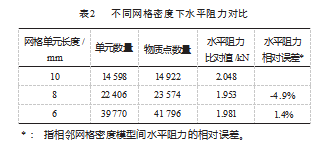
6 mm 单元组水平阻力和垂直阻力随时间变化曲线如 图 6 所示。水平阻力和垂直阻力在 4 s 后接近平稳, 与文 献[18]试验结果符合, 参照文献[18], 将第 5 s 内 (对应刀 具运动距离为 200~250 mm 范围) 的均值作为测量值。由 于水平阻力远大于垂直阻力, 因此水平阻力更适合作为 网格收敛性依据。 3 组模型水平阻力测量值和相对误差 记录在表 2 中。可以看到, 水平阻力及其相对误差绝对 值随着网格密度的增大而减小, 且当单元长度为 6 mm 时, 其相对误差小于 2%, 可以认为其精度是足够的, 因 此后续仿真模型中将网格单元长度均设定为 6 mm。
3.2 土壤变形分析
3.2.1 土壤切削过程分析
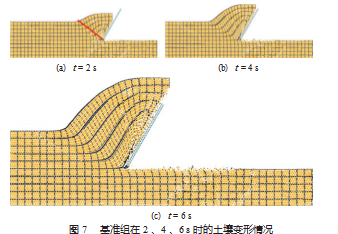
为更好地观察和描述土壤变形, 使用间距为 20 mm 网格对土壤进行划分并跟踪物质点的运动轨迹, 得到基 准组在 2 、4 、6 s 时的土壤变形情况, 如图 7 所示。
在刀具开始运动后, 率先与刀具接触的土壤沿着刀 面向上流动。由于刀具切向黏着力的作用, 靠近刀具表 面的土壤沿着刀面切向速度较小, 远离刀具表面的土壤 受到影响较小因而切向速度较大, 较大的速度梯度致使 在刀具表面附近网格扭曲严重。在土壤基底和土壤切层 之间会形成一个明显且稳定的剪切平面, 如图 7 (a) 中 红线所示。在剪切平面附近网格严重扭曲, 土壤发生剪 切破坏, 但并无明显剪切裂痕, 与图 8 试验结果吻合。 随着刀具继续向前移动, 不断有新的土壤因剪切破坏而 失效, 之前失效的土壤被推挤着沿刀面向上移动。如此 持续进行, 刀面前部土壤呈现出流动状态。
3.2.2 网格变形分析
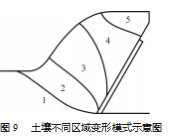
基准组实物试验中土壤变形情况如图 8 (a) 所示, 比较基准组仿真和试验中网格的变形情况, 可以将变形 区域划分为如图 9 所示的 5 个区域。
为 方 便 描 述 网 格 变形, 将初始水平的网格线称为 Ⅰ 线, 而将初始垂直的网格线称为Ⅱ线。区 域 1 为 土 壤 基 底, 网格没有明显变形。区域 2土壤受剪切失效, 网格开始变形, 该区中 Ⅰ 线逐渐由水平方向转到刀面切向方 向, Ⅱ线逐渐由垂直方向过渡到区域 3 中 Ⅱ线的方向。 区域 3 中 Ⅰ 线与刀面平行, Ⅱ线之间相互平行, 且Ⅱ线 与垂直方向夹角近似和刀面与垂直方向夹角相等。区域 4 土壤受到刀具切线黏着力影响严重, Ⅰ 线由与刀面平 行方向过渡到与刀面垂直方向, Ⅱ线则从区域 4 底角向 上成放射状。区域 5 处土壤被整体推挤沿刀面运动, 网 格无明显变形。
根据上述分析并对比图 7 (c) 和图 8. 可以看到仿 真和试验结果在区域 1 、2 和 3 具有高度一致性, 在区域 4. 仿真结果中的 Ⅰ线弯曲变形程度略低于试验结果。区 域 5 由于试验照片未能覆盖到, 无法进行直接比较, 但 文献[22]进行了类似试验, 结果表明区域 5 的确无明显 变形。
3.2.3 剪切角、剪切长度试验和仿真结果对比
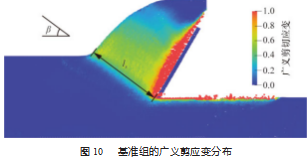
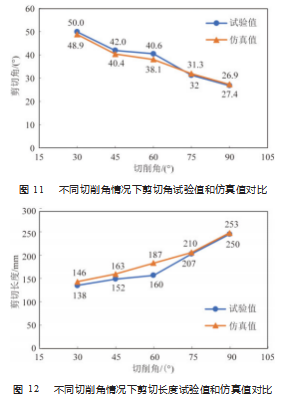
为确定仿真模拟的剪切面, 绘制了广义剪应力分布 如图 10 所示。从图中可以方便地确定剪切面的位置和方向。将剪切面与水平面的夹角称为剪切角 β, 将土壤切 层在剪切面上的投影长度定义为剪切长度 ls, 在图 10 中 分别标注。为对土壤变形进行更加精确的定量分析, 将不同切 削角情况下剪切角、剪切长度的试验值和仿真值绘制在 图 11~12 中。从图中可以看出, 仿真值和试验值变化趋 势相同, 即剪切角随着切削角的增大而减小, 剪切长度 随着切削角的增大而增大。从定量结果可进一步看出,仿 真值和试验值一致性较高, 剪切角误差不超过 2.5°, 剪切 长度平均误差为 10.4 mm。尤其是在切削角较大时 ( α ≥ 75°), 剪切角误差不超过 1°, 剪切长度误差仅为 3 mm。
3.3 切削阻力分析
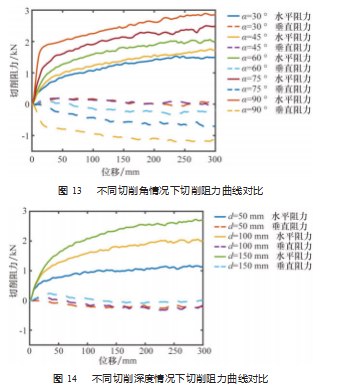
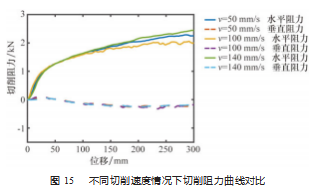
9 组仿真中切削阻力随刀具位移曲线如图 13~15 所 示。从图中可以看出, 水平阻力随切削角度、切削深度 的增大而增大, 而切削速度对水平阻力的影响微弱, 与 文献[18]中试验结果相符。
水平阻力曲线可近似看成两段直线的组合, 在第 1 个直线阶段, 水平阻力上升较快, 而在第 2 个直线阶段, 水平阻力上升较慢。根据图 13 可知, 切削角度增大, 会 提高第 1 个阶段水平阻力的上升斜率, 同时缩小达到第 2 个阶段的时间, 但是却几乎不影响第 2 个阶段水平阻力 的上升斜率。根据图 14 可知, 切削深度对第 1 阶段的水 平阻力上升斜率影响不大, 而第 2 阶段的水平阻力上升 斜率与切削深度正相关。根据上面分析并结合土壤变形 可知, 在第 2 个阶段, 切削进入稳定状态, 水平阻力缓 慢上升是由于土壤剪切失效后流向刀面前部并逐渐积累 造成的。
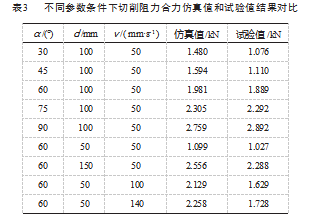
对于垂直阻力, 切削角度的影响最为明显, 切削深 度和切削速度的影响较小。垂直阻力相对水平阻力较小, 但当切削角度较大时, 垂直阻力将迅速增大。值得注意 的是, 在切削角度较小时, 垂直阻力会出现正值, 即垂 直阻力垂直向下, 此情况会对刀具的安装条件有所限制。为验证物质点法在土壤切削过程中刀具切削阻力预 测方面的有效性, 将仿真结果 200~250 mm 处切削阻力合 力的均值作为测量值, 与文献[18]试验结果进行对比, 如表 3 所示。从表中可以看到, 仿真在切削角较大 ( α ≥ 60°) 时对切削阻力合力的预测较为准确, 平均误差为 3.4%。单纯看仿真值或试验值, 切削速度对切削力的影 响较小, 但是仿真值随切削速度的增大而缓慢增大, 符 合文献[23]公式计算结果, 而试验值随切削速度先减小 后增大。
对于切削角较小时, 仿真预测结果偏大的原因是不 同的失效模式造成的。在文献[18]中强调了当切削角 α > 45° 时, 切削产生剪切失效, 如图 8 (a) 所示, 而 α ≤ 45° 时, 切削产生撕裂失效, 如图 8 (b) 所示。根据文 献[23], 在剪切失效和撕裂失效的临界状态, 撕裂失效 情况下无论水平阻力还是垂直阻力均低于剪切失效对应 阻力, 这也正是仿真值和试验值的差别。
考虑撕裂失效是由于土壤裂纹不断扩展形成的, 而 Anura3D 目前并无裂纹及其扩展算法, 因而仿真未能形 成撕裂失效模式, 所以进一步开发物质点法裂纹相关算 法将有助于得到更加精确的土壤切削过程数值模拟。
4 结束语
本文基于 Anura3D 软件, 建立了土壤切削过程的物 质点法仿真模型。详细说明了切削过程中土壤的变形及 演化过程, 分析了土壤切削参数包括切削角度, 切削深 度和切削速度对剪切角, 剪切长度和切削阻力等的影响。 通过与试验数据对比, 所建模型可以较为准确地预测土 壤变形和切削阻力, 剪切角误差不超过 2.5°, 剪切长度 平均误差 10.4 mm; 在土壤发生剪切失效时, 切削阻力 预测平均误差 3.4%。验证了物质点法在土壤切削过程模 拟的可行性与有效性。物质点法模型中土壤参数获取简 单, 不存在网格畸变问题, 无需预先指定失效面, 克服 了常见计算方法的缺点, 为研究土壤切削过程提供了新 思路。
在当前 Anura3D 算法框架下, 由于缺乏裂纹相关 算法, 在切削角度较小时, 未能模拟出撕裂失效模式, 切削阻力预测精度下降。因此有必要进一步开发裂纹 相关算法, 以得到更加精确的土壤切削过程数值模拟 结果。
参考文献:
[1] AHMED ELBASHIR M, ZHAO Z, AHMED HEBEIL E, et al. Comparative finite element analysis of the effects of tillage tool geometry on soil disturbance and reaction forces[J]. Research Journal of Applied Sciences, Engineering and Technology, 2014. 7(15): 3145-3149.
[2] DAVOUDI S, ALIMARDANI R, KEYHANI A, et al. A two di⁃ mensional finite element analysis of a plane tillage tool in soil us ⁃ ing a non-linear elasto-plastic model[J]. American-Eurasian Journal of Agricultural and Environmental Sciences, 2008. 3(3): 498-505.
[3] FIELKE J M. Finite element modelling of the interaction of the cutting edge of tillage implements with soil[J]. Journal of Agricul⁃ tural Engineering Research, 1999. 74(1): 91- 101.
[4] ARMIN A, FOTOUHI R, SZYSZKOWSKI W. On the FE model⁃ ing of soil-blade interaction in tillage operations[J]. Finite Ele⁃ ments in Analysis and Design, 2014. 92: 1- 11.
[5] ABO-ELNOR M, HAMILTON R, BOYLE J T. 3D dynamic anal⁃ ysis of soil-tool interaction using the finite element method[J]. Journal of Terramechanics, 2003. 40(1): 51-62.
[6] LYSYCH M N. Review of numerical methods for modeling the in ⁃ teraction of soil environments with the tools of soil tillage ma⁃ chines[J]. Journal of Physics: Conference Series, 2019. 1399(4): 044014.
[7] MAK J, CHEN Y, SADEK M A. Determining parameters of a dis ⁃ crete element model for soil-tool interaction[J]. Soil and Tillage Research, 2012. 118: 117- 122.
[8] SULSKY D, CHEN Z, SCHREYER H L. A particle method for history-dependent materials[J]. Computer Methods in Applied Mechanics and Engineering, 1994. 118(1): 179- 196.
[9] 张雄, 廉艳平, 刘岩, 等 . 物质点法[M]. 北京: 清华大学出版社,2013.
[10] 吴博 . 物质点法与壳单元的耦合及其在鸟撞问题中的应用 [D]. 北京: 清华大学, 2016.
[11] 谷骁勇 . 金属高速及超高速切削的物质点法数值模拟技术 研究[D]. 北京: 北京理工大学, 2016.
[12] GIRARDI V, CECCATO F, ROHE A, et al. Failure of levees in⁃ duced by toe uplift: Investigation of post-failure behavior using material point method[J]. Journal of Rock Mechanics and Geo ⁃ technical Engineering, 2022.
[13] De VAUCORBEIL A, NGUYEN V P, SINAIE S, et al. Material
关注SCI论文创作发表,寻求SCI论文修改润色、SCI论文代发表等服务支撑,请锁定SCI论文网!
文章出自SCI论文网转载请注明出处:https://www.lunwensci.com/ligonglunwen/63649.html