SCI论文(www.lunwensci.com)
摘要:安装在风电机组机舱尾部的风速仪会受到风轮尾流和机舱形状影响, 无法直接用于功率曲线测试, 国际电工委员会在标准 文件 IEC 1400- 12-2:2013 中给出的区间拟合法 (Binned-NTF) 准确性不高。应用随机森林方法拟合机舱传递函数, 分析了海上和 陆上的多个机型的实测数据, 对比 IEC 方法, 在均方根误差 (RMSE)、平均绝对误差 (MAE)、拟合精度 R2 等指标上均有较大改 善。功率曲线趋势曲线的拟合均方根误差从 0.2~0.5 降低到 0. 1~0.3. 发电量评估的误差从 0.4% ~ 8.2% 降低到-3. 1% ~ 0.2%。研究表 明影响机舱传递函数的主要特征为风速、功率和变桨角。对 8 个项目的功率曲线测试数据进行分析, 发现变桨角的重要系数随测 试数据集中变桨的数据量百分比的升高而增加, 该方法简单易用, 为提升机舱传递函数估计的准确度提供了有效支持。
关键词:机舱传递函数,功率曲线测试,随机森林,特征重要系数
Estimation of Wind Turbine Nacelle Transfer Function Based on Random Forest
He Yuxiang, Chen Baokang, Liu Yongqiang
(Ming Yang Smart Energy Group Limited, Zhongshan, Guangdong 528400. China)
Abstract: The anemometer installed at the tail of the wind turbine nacelle will be affected by the rotor wake of the wind turbine and the shape of the nacelle, and cannot be directly used for power curve test. The accuracy of binned NTF given by the International Electrotechnical Commission in the standard document IEC 61400- 12-2: 2013 is not high. The random forest method was used to fit the nacelle transfer function, and the measured data of several offshore and onshore wind turbines were analyzed . Compared with IEC method, it had greatly improved the root mean square error (RMSE), mean absolute error (MAE), fitting accuracy R2 and other indicators. The root mean square error of fitting power curve trend curve was reduced from 0.2~0.5 to 0. 1~0.3. The error of power generation was reduced from 0.4% ~ 8.2% to -3. 1% ~ 0.2%. The research shows that the main characteristics affecting the nacelle transfer function are wind speed, power and pitch angle. By analyzing the power curve test data of 8 items, it was found that the important coefficient of pitch angle increased with the increase of the
percentage of pitch data in the test data set. The method is simple and easy to use, which provides effective support for improving the accuracy of nacelle transfer function estimation.
Key words: nacelle transfer function; power curve test; random forest; characteristic importance coefficient
引言
风电机组的功率曲线是评估风电机组发电量的重要 指标[1], 依据国家标准 GB/T 18451.2-2021 标准要求, 风 电机组功率曲线测试需要在被测机组主风向上 2 ~ 4 倍风 轮直径的距离上设置测风塔[2], 配置测风塔对场地要求 严格, 测试费用高昂, 场地评估时间较长。而安装在风 电机组机舱尾部的机舱风速仪测得的风速受到了自身测 量误差[3] 以及风轮转动和机舱形状的影响, 导致气流发 生畸变, 机舱周边的某些区域因壁面效应出现“增速 区”[4-5]。文献[6]指出, 机舱风速收到叶片转速影响, 低 风速时受湍流影响大, 高风速时机舱尾部尾流影响明显 大于稳定来流的影响。以上诸多因素决定了不能直接应 用机舱风速作为功率曲线测试的风速数据。实际工程应 用中一般选取风场中一台机组作为测试对象, 以它的功率特性评估整个风场所有机组的功率特性, 这就造成了 很大的随机性和不确定性[7]。如果为每台风机都设立测 风塔, 经济成本和测试时间成本又过高, 因此, 利用机 舱风速评估机组功率曲线具有成本低、耗时短、数据相 对容易获取等明显优势。
机舱风速与测风塔风速的函数关系被称为机舱传递 函数 (Nacelle Transfer Function, NTF ), IEC 61400- 12-2 标 准 利 用 根 据 给 出 了 的 分 区 间 的 机 舱 传 递 函 数 模 型 (Binned NTF), 该方法规避了理论仿真偏差大、难以应 用的问题[8], 但也存在区间个数较多, 应用不便等不足。 该方法本质上仅为曲线分段线性拟合, 并没有严格的理 论证明, 也无法得知影响机舱传递函数的主要特征量。 实际工程应用中, 为了适应识别精度和易用性的要求, 有很多专家提出了针对 IEC 标准的区间法的替代或改进方法。文献[8]分析了理论修正方法的误差原因, 对比了 IEC 区间拟合法和单区间拟合法的精度和易用性, 提出 一种高次多项式分区拟合的机舱传递函数拟合法, 达到 了较高的拟合优度, 给出了拟合方程, 并给出过渡区拟 合异常的解决方案。文献[9]分析了湍流强度对 IEC 区间 法的影响, 指出高湍流和低湍流对各区间的拟合斜率和 截距影响不同, 并利用 380 h 的测试数据, 按“高湍流” 和“低湍流”分别拟合机舱传递函数, 提高了拟合精度。 文献[10]应用深度学习技术, 利用一维卷积神经网络进 行拟合, 降低了发电量误差率。
为了提高机舱传递函数模型的识别精度, 并探究 NTF 拟合过程中的主导特征, 本文提出一种基于随机森 林的机器学习机舱风速修正方法, 构建机舱风速修正模 型。随机森林方法具有高准确率, 训练速度快, 不容易 过拟合、可得到变量重要性排序等优势[11- 12], 一定程度 规避了神经网络的特征可解释性差、训练开销大和过拟 合问题[13], 可获得较高拟合精度。本文以一台 3.6 MW 机 组作为工程应用实例, 利用随机森林方法与 IEC 区间法 的拟合结果进行对比, 并利用 8 个不同风场条件下的测 试项目, 评估影响机舱传递函数准确性的主导因素。
1 IEC 区间法
根据IEC 61400- 12-2 标准, 利用式 (1) 和式 (2) 计 算出各个bin区间内的机舱风速平均值和测风塔风速平均值。
2 随机森林
随机森林的基础是决策树算法, 决策树算法是一种 基于实例的算法, 是一种自上而下的归纳过程[14]。随机 森林是随机数据采样和随机特征选定的大量决策树的集 合, 利用 bootstrap 抽样从训练集中有放回地随机选择 n 个数据集, 并分别训练 n 个分类器。训练数据集中允许 出现重复数据, 也允许有从未使用的数据。这些从未使 用的数据被称为袋外数据 (Out of Bag, OOB), 由于没有参与训练, 因此可被用来检测模型的泛化能力。随机 森林算法为每个样本创建一个决策树, 再对每个分类结 果进行投票, 决出每个样本所处的最优分类。多个决策 树比单个决策树具备更高的可靠性, 并通过对结果求平 均值降低了过拟合风险。与深度学习方法对比, 具有计 算开销低、对噪声、异常值不敏感、可解释性强等优点, 可给出自变量和因变量之间的任何非线性关系,避免了深 度学习方法可解释性差的缺陷, 适用于本文的研究内容。
3 模型训练与估计流程
对于机舱传递函数的识别, 首先需要将测试数据标 准化, 然后进行试训练, 筛选主要相关变量, 再以数据 集和测试集 8 ∶2 的比例进行训练, 验证模型的正确性, 最后按照 IEC 标准要求通过自我一致性检查。基于随机 森林的风电机组机舱传递函数估计方法流程如图 2 所示。
为了验证随机森林方法的拟合精度, 本文研究对象 包括 8 组不同风场的风机, 根据国家标准 GB/T 18451.2— 2021 的要求, 功率曲线测试需要先对场地地形进行评 估。陆上项目一般需要进行场地评估, 对于复杂地形需 要进行场地风速标定, 海上测风一般使用激光雷达[15]。 测试数据需要进行筛选, 需要剔除的数据包括停机工况、 限功率工况、非可用扇区、切出风速等无效数据。
4 工程实例与 NTF 拟合精度对比
4.1 项目信息
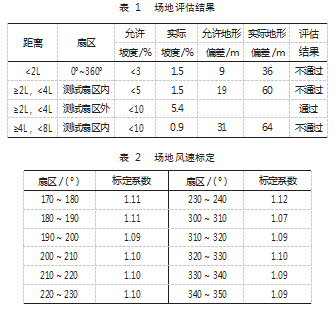
以内蒙东部一台 3.6 MW 机组作为实验对象, 额定功率 3 600 kW, 额定风速 10.9 m/s, 轮毂中心高度 90 m, 风轮直径 133 m, 测风塔与风机距离为 343 m, 满足标准 要求的测风塔与风机距离 2~4 倍风轮直径的要求。可用 扇区为 170°~240°和 300°~350° 。现场地形为复杂地形, 需要进行场地风速标定, 表 1 为场地评估结果, 表 2 为风 速标定系数。测试时间为 2019 年 3 月-6 月。
4.2 测试数据标准化与预处理
为了统一数据标准, 应用式 (4) 将气压校正到轮毂 高度的气压, 应用式 (5) 将风速标准化到标准空气密度 ( 1.225 kg/m3 ) 下的风速。
数据标准化后, 剔除不可用扇区、停机工况、限功 率工况、不合理结果 (如激光雷达风速异常测试值) 以及其他非正常工况的数据, 将筛选后的数据应用随机森 林方法拟合机舱传递函数。
图 4所示为机组的风速功率散点图, 图 5 所示为机舱 风速与测风塔风速的关系, 可见, 本项目的机舱风速与 测风塔风速有一定相关性, 且分布在测风塔风速两侧, 并没有明显的偏大或偏小的趋向性。
4.3 模型参数调优
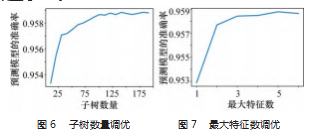
本项目应用参数迭代方法调优, 避免了网格搜索对 资源和时间消耗较大的缺陷[18]。以机舱风速、功率、发 电机转速、湍流、桨距角、风剪切共 6 个特征训练模型, 将待拟合数据按 8 ∶2 的比例划分为训练集和测试集。首 先调节子树数量, 由图 6 可知, 随着子树数量的增加, 测试数据模型拟合的准确率逐渐增大, 当越过最佳子树 数量后, 出现过拟合, 准确率逐渐下降, 本次设定子树 数量为 120.
在此基础上对最大特征数调优, 图 7 所示为模型准 确率与最大特征数的关系, 这里取 5.
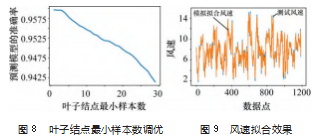
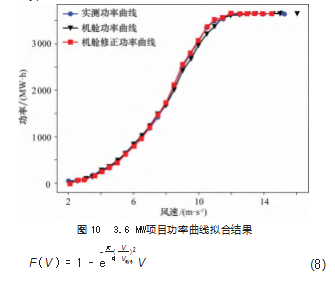
在此基础上对叶子结点最小样本数调优, 由图 8 可 知, 随着叶子结点样本数增加, 模型预测精度降低。本 次设定叶子结点最小样本数为 1.应用以上参数, 训练 得到模型的准确率达到 0.961. 得到风速拟合曲线, 如图 9 所示。
4.4 拟合精度验证
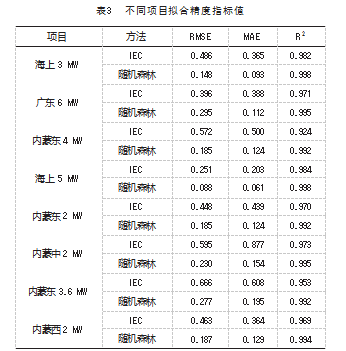
以均方根误差 (Root Mean Square Error, RMSE) 平 均绝对误差 (Mean Absolute Error, MAE) 和拟合优度 R2( R-squared, R2 ) 3 个指标描述各种拟合方法的拟合精 度。表 3显示本方法在 8个不同风场环境下的拟合精度指 标值均优于 IEC方法的拟合精度。
图 10 所示为内蒙东部 3.6 MW 项目功率曲线, 以该 项目为例, 对比发电量拟合效果, 对 NTF进行自我一致 性检查。式 (8) 为瑞利累积分布公式, 式 (9) 为发电 量计算公式。
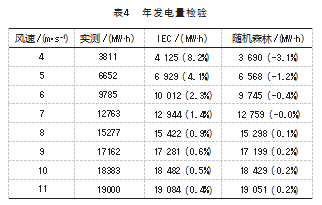
表 4所示为 4 ~ 11 m/s 每个风速段的发电量大小, 单 位为兆瓦时 (MW·h), 括号为与实测值的相对误差百分 比。由表可知, 随机森林方法的拟合 RMS误差在-3.1% ~ 0.2%, IEC方法 RMS误差在 0.4% ~ 8.2%, 并且在每一 个风速区间内, 随机森林方法的 RMS误差均低于 IEC标准的区间法, 验证了本方法的拟合精度。
5 NTF 主导特征分析
当前工程应用中, 对 NTF 的估计一般仅限于曲线拟 合, 并没有研究风机各特征量对 NTF 的贡献量。本节依 据试验数据讨论不同项目的 NTF 主导特征与数据量以及 测试环境之间的关系。
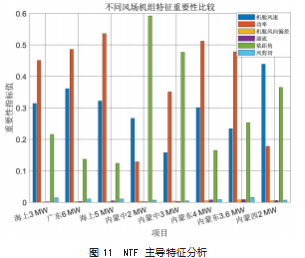
不同的特征对随机森林模型的贡献量不同, 而模型 的预测能力依赖于贡献较大的特征。将上述 8个项目的 特征重要性系数绘图对比, 由图 11可见, 机舱风速、功 率和变桨角是影响机舱传递函数的主导因素, 其他特征影响力微弱。其中变桨角的重要性系数在不同项目中差 异较大, 需要进一步讨论。
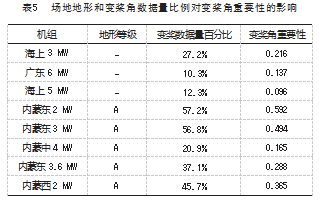
深入分析变桨角的重要程度与地形和变桨数据量百 分比的关系。如表 5所示, 地形对变桨特征的重要性影 响不明显, 观察图 12 的规律, 发现随着变桨角数据量百 分比的增加, 变桨角的对训练模型的重要性程度有增加 的趋势。
当机组在测试期间长期处于额定功率及以上运行状 态时, 机组桨叶角度处于收桨一定角度的状态, 变桨角 的数据量增多, 变桨角的其重要性系数就会升高; 反之, 当测试期间机组长期处于低功率及额定功率以下运行状 态时, 变桨角的影响系数就会下降。这就要求同风场 同机型机组在应用 NTF 时, 需要考虑整体数据量的构 成比例。
5 结束语
应用随机森林方法对多个风场不同项目的风电机组 机舱传递函数进行拟合, 形成以下结论。
( 1) 以某 3.6 MW风机功率曲线测试数据验证了随机 森林方法的精度高于 IEC 方法, 说明了随机森林方法的 可行性。
( 2) 将基于随机森林的风电机组机舱传递函数估计 方法分别应用在不同风场、不同机型、不同功率的测试 项目中, 进行机舱传递函数的拟合, RMSE、MAE、R2 等各项拟合精度指标均高于 IEC 方法, 验证了本方法的 通用性。
( 3) 对影响机舱传递函数的主导特征进行了研究, 发现主导特征为机舱风速、功率和变桨角。
( 4) 不同项目之间, 变桨角的重要系数差异较大, 通过分析发现其重要程度随着测试数据集的变桨数据量 百分比的增加而上升。可以认为, 随着高功率工况测试 点的增加, 变桨角对训练的模型的影响程度会增加, 甚 至起到主导作用。
参考文献:
[1] 刘昊 . 大型风电机组综合性能评估方法研究[D]. 北京:华北电 力大学(北京),2009.
[2] GB/T 18451.2—2021. 风力发电机组功率特性测试[S].
[3] 姜文玲,冯双磊,孙勇,等 .基于机舱风速数据的风电场弃风电 量计算方法研究[J]. 电网技术,2014.38(3):647-652.
[4] Ameur K,Masson C,Eecen P J.2D and 3D numerical simulation of the wind-rotor nacelle interaction in an atmospheric boundary layer[J].Journal of Wind Engineering and Industrial Aerodynam ⁃ ics,2011.99(8):833-844.
[5] 田琳琳,赵宁,钟伟 .风力机尾流相互干扰的数值模拟[J]. 太阳 能学报, 2012. 33(8):6.
[6] 丁林 . 风力机机舱近尾流数值模拟研究[D]. 北京:华北电力大 学(北京),2019.
[7] 娄建楼,胥佳,单凯,等 .基于机舱风速计的风电机组功率特性 评估方法[J]. 电力系统自动化,2016.40(9):23-28.
[8] 高峰,杨锡运,王伟,等 .基于测风塔测风数据的风电机组机舱 风速修正[J]. 系统仿真学报,2016.28(11):2790-2797.
[9] 张双益,胡非 .基于湍流的双 NTF 方法应用于机舱风速计测量 功率曲线[J]. 可再生能源,2017.35(7):1072-1080.
[10] 杨明明 . 基于卷积神经网络的机舱风速修正[J]. 华电技术 , 2021.43(5):75-79.
[11] 曹桃云 . 基于随机森林的变量重要性研究[J]. 统计与决策 , 2022.38(4):60-63.
[12] 杜尚海,古成科,张文静 . 随机森林理论及其在水文地质领域 的研究进展[J]. 中国环境科学:1-12[2022-06-06].
[13] 马璐瑶 . 基于随机森林和 BP神经网络的个人信用评估比较 分析[D]. 济南:山东大学,2020.
[14] 黄海新 ,吴迪 ,文峰 . 决策森林研究综述[J]. 电子技术应用 , 2016.42(12):5-9.
[15] 石宇峰,何宇翔,魏煜锋 .激光雷达在海上风电机组功率曲线 测量中的应用可行性[J].船舶工程,2020(S01):3.
[16] 黄思岚,杨杰,屈旭东 .基于 NRS-RF 的混凝土坝变形监测模 型研究[J].人民长江,2021.52(2):111-116.
[17] 王仁超,朱品光 .基于随机森林回归方法的爆破块度预测模 型研究[J]. 水力发电学报,2020.39(1):89-101.
[18] 高虹雷, 门昌骞,王文剑 . 多核贝叶斯优化的模型决策树算法 [J]. 国防科技大学学报,2022. 44(3): 67-76.
关注SCI论文创作发表,寻求SCI论文修改润色、SCI论文代发表等服务支撑,请锁定SCI论文网!
文章出自SCI论文网转载请注明出处:https://www.lunwensci.com/ligonglunwen/63580.html