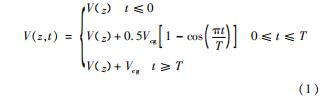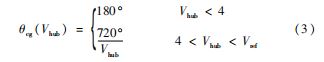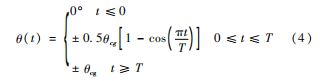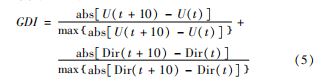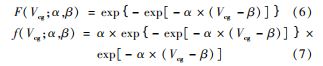SCI论文(www.lunwensci.com)
摘要:IEC61400-1 标准中提出了对于特定场址评估,可以采用特定场址的风向变化的极端相干阵风模型(ECDs ),但是标准中未明 确具体的取值方法。基于此,从统计学出发得到一种风速和风向同时变换的ECDs 模型阵风幅值确定方法。基于特定场址项目的 SCADA 数据,通过判断风向变化阵风指数(GDI ) 的大小筛选出满足IEC 标准要求的阵风样本,然后使用统计学方法得到五十年一 遇重现期内的阵风最大值,并分析其对载荷的影响。结果表明,采用甘布尔分布拟合结果良好,SCADA 数据时长对结果有影响需 要采用一年以上数据,相同项目不同机位点之间ECDs 阵风幅值同样存在差异,不同项目之间ECDs 阵风幅值差异较大,对于简单 地形的项目,湍流强度期望值和平均风速越低则项目ECDs 阵风幅值越低,反之ECDs 阵风幅值越高。
Research on Analysis Methods of ECDs Gust in Specific Sites
Liu Wei 1.2.Wang Ruiliang1.2.Sun Yong1.2.Zhang Peicheng1.2.Zhang Yuan 1.2
( 1.Zhejiang Windey Co.,Ltd.,Hangzhou 310012.China;
2.Zhejiang Key Laboratory of Wind Power Generation Technology,Hangzhou 310012.China )
Abstract:The evaluation model in specific sites has been proposed in the IEC61400-1 standard.The standard shows that ECDs gust model can be used in specific sites analysis.However,the value determining method has not yet been clearly defined.From statistics,a method is proposed for determining the gust amplitude of ECDs model with simultaneous transformation of wind speed and direction.Based on SCADA ( Supervisory Control and Data Acquisition ) data for specific sites,the gust samples meeting the requirements of IEC standard have been selected through evaluating the value of Gust Directional Index ( GDI ).Then the maximum gust with a recurrence of 50 years is obtained by using statistic method and the influence on loads is analyzed in the last part.The results show that the fitting results using Gumbel distribution are well.The SCADA data duration has an impact on the evaluations,which requires data more than one year.There are also differences in ECDs gust amplitudes between different locations in the same site.Furthermore,here is great difference in ECDs gust amplitude between different projects.For simple terrain,the lower value of expected turbulence intensity and average wind speed is,the lower ECDs gust amplitude is,inversely,the ECDs gust amplitude will be higher.
Key words:wind turbine;IEC standard;ECDs;gust amplitude;Gumbel distribution
0 引言
十三五”以来中国风电飞速发展,为响应“十四 五”规划,实现“碳达峰”“碳中和”的目标,风电机 组的叶轮直径不断增大,机组容量不断提高,塔筒的高 度也在不断提升,同时市场竞争日益激烈,这些对载荷的挑战也越来越高。而载荷计算必须依据一定的工况和 外部环境条件进行分析[1-3],这就需要一系列的风模型,常规风模型分为正常风模型和极端风模型,本文主要基于IEC61400-1[4 ] 标准中的伴随风向变化的极端运行阵风 ( ECD ) 模型,从特定场址实际风况条件出发,运用统计学的方法,旨在找到一种特定场址的风向变化的极端相 干阵风模型(ECDs ) 模型的阵风幅值确定方法。目前载荷计算使用的国际通用标准主要有国际电工委员会标准IEC 61400-1 、挪威船级社DNV 规范[5]和德国船级社GL 规范[6-7 ] 等,同时各国从自身条件和经验出发也制定了相应标准,如中国船级社风电机组规范[8]等, 这些大都通过IEC 61400-1 标准转化而来,总体差异不 大。同一个标准中随着时间推移存在多个版本,比如 IEC 61400-1 标准存在1999 年修订的第二版标准,2005 年修订的第三版标准,2019 年修订的第四版标准。对于 载荷计算的通用标准,不管哪种标准规范或者标准均存 在伴随风向变化的极端运行阵风(ECD ) 模型,这是评 估风力发电机组载荷极限情况的一个非常重要的极限风 模型。
IEC61400-1 标准中指出可以采用特定场址的风向变 化的极端相干阵风模型(ECDs ) 来仿真特定场址载荷, 但是标准中没有明确具体的方法。对于大部分简单地形 的项目,风向变化的极端相干阵风模型(ECD ) 是限制载荷与塔架重量的一个非常重要的条件,因此研究如何 确定简单地形地区的特定场址的风向变化的极端相干阵 风模型(ECDs ),具有非常重要的意义。
本文基于特定场址项目的SCADA 数据,通过判断阵 风风向指数(GDI ) 的大小筛选出满足IEC 标准要求的 阵风样本,然后通过统计学方法得到五十年一遇重现期 内的阵风最大值,并分析其对载荷的影响。
1 ECDs 阵风幅值确定方法
1.1 ECD 阵风模型介绍
ECD 阵风模型是风力发电机组载荷仿真中的非常关 键的模型,其对轮毂、机架和塔架等部件极限载荷影响 较大。IEC61400-1 标准中定义了标准形式的ECD 模型,其阵风幅值Vcg 为15 m/s,风速的计算公式如下:
其中持续时间T= 10 s,z 为距地面高度,V (z )正常风廓线(NWP ) 给出,正常风廓线公式如下:
式中:Vhub 为轮毂中心高度处风速;zhub 为轮毂中心高度; α 为风切变。
ECD 模型中假定的是风速上升与风向变化是同步进 行的,其幅值θcg 公式如下:
式中:Vref 为机组参考风速。
风向的变化公式由下式给出:
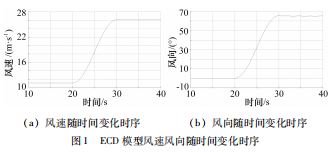
其中持续时间T=10 s。风速(11 m/s ) 风向随时间 变化时序图如图1所示。
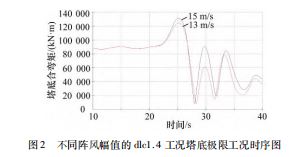
阵风模型,该工况经常是风力发电机组塔架设计的瓶颈工况[9-11 ],这里以某5MW 机组130 m 塔底载荷为例,图 2 分别是采用15 m/s 阵风幅值和13 m/s 的ECD 阵风幅值 的塔底合弯矩。从图中可以发现阵风幅值从15 m/s 降低至 13 m/s,塔底合弯矩有明显降低,其值从130 684 kN ·m降 低至124 301 kN ·m,降幅接近5%,对于该款塔架整体 质量会降低10 t 以上,相当于单台机组节省了接近10 万 元,其带来的经济效益相当可观。
IEC61400-1标准中仅规定了标况下的ECD阵风模型,针对特定场址的ECDs 阵风模型标准中仅提出可以 采用,但是未给出详细定义。本文主要通过实测的 SCADA 数据筛选出符合风速风向同时变换的数据,然后 通过该数据推导出五十年一遇情况下的ECDs 阵风幅值。
1.2 ECDs 阵风幅值确定方法
特定场址的风向变化的极端相干阵风(ECDs ) 在实际过程中发生次数有限,本文基于风电场大量的实测 SCADA 数据进行分析,引入风向变化阵风指数[12]( GDI ),如下式所示:
这里的U ( t ) 是实测的风速,Dir ( t ) 是实测的风向,分母中最大值是实测十分钟内差值的最大值。对于 给定实测序列,GDI 的最大值在[1∶ 2 ] 之间,如果值为1 则表示风速风向完全不相关,如果值为2则表示风速风 向完全相关。本文中筛选所有GDI 大于1.98 的数据点, 大于1.98 的数据点风速风向有很强的相关性,如果仅取 值为2的点,则数据点数会非常少,影响数据的稳定性。
将符合条件的值值对应的10 s 风速差累积分布,并通过甘布尔(Gumbel ) 分布拟合得到累积概率密度函数F(式(6 )),求导得到相应的概率密度函数f(式(7 ))。
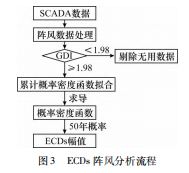
然后根据筛选得到的满足GDI 大于1.98 的样本数 Ng,以及总样本数Nt 和五十年一遇概率P50 得到特定场址ECDs 模型的五十年一遇分位数Pcg 50 为Nt/( Ng ·P50)。然后通过概率密度函数f推导出特定场址ECDs 的阵风幅值Vcg 50.ECDs 阵风分析流程如图3所示。
2 ECDs 阵风幅值结果与分析
本文随机选择简单地形的8个风电场项目,每个项 目选择大于3 台的机位点进行数据分析。首先使用 Python 程序对风电场项目的风速和风向数据进行筛选, 找出满足GDI 大于1.98 的数据点,得到各机位点的满足 要求的样本数Ng,以及总样本数Nt 从而推算出各个机 位点的Pcg 50 分位数。然后通过Matlab 软件使用甘布尔 函数拟合分析满足GDI 大于1.98 的样本,求导得到对应 的概率密度函数,最终得到该机位点的阵风幅值Vcg 50.
本节主要从单个机位点的ECDs 阵风幅值结果、相 同项目不同机位点ECDs 阵风幅值结果、不同数据时长 对ECDs 幅值结果的影响和不同项目ECDs 阵风幅值结果4 个方面分析不同情况下的ECDs 阵风幅值。
2.1 单个机位点ECDs 阵风幅值结果分析
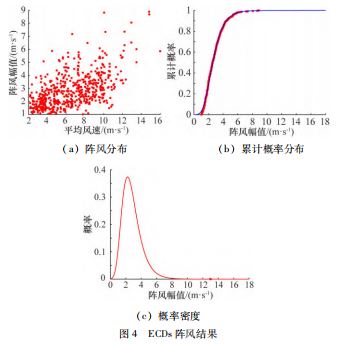
本节首先随机选择单个简单地形的项目的其中一个 机位点按上述方法进行分析,其阵风结果如图4所示。
图4 ( a ) 为该机位点SCADA 数据中满足GDI 大于1.98 的阵风幅值及其对应的10 min 平均风速,从该散点 图可以发现统计出来满足GDI 大于1.98 的阵风幅值最大 值为8.9 m/s,阵风幅值与该风速所处时候的10 min 平均风速正相关。
图4 ( b ) 为筛选后的阵风幅值累计概率分布结果,红色数据为筛选出的实测阵风幅值数据,蓝色曲 线为采用甘布尔分布拟合得到的曲线,拟合的相关系 数R2 =0.993.总体相关性良好,能较好地反映实际阵风幅值的分布情况。
图4 ( c ) 为甘布尔分布拟合曲线求导得到的概率密度曲线,结合筛选出的样本数Ng,以及总样本数Nt 和五十年一遇概率P50 得到特定场址ECDs 模型的五十年一遇分位数Pcg 50 为Nt/( Ng ·P50 )。然后通过概率密度函数f推导出特定场址ECDs 的阵风幅值Vcg 50 = 13.0 m/ s,比标准ECD 模型的15 m/s 阵风幅值小2m/s,采用13 m/s 的ECDs 阵风模型进行载荷仿真能有效的降低风力发 电机组的整机与塔架载荷。
2.2 相同项目不同机位点ECDs 阵风幅值结果分析
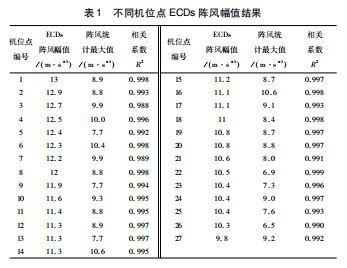
针对单个风电场项目,不同机位点之间由于地形、 尾流等原因,各个机位点的风资源情况会存在差异,这 里基于单个项目不同机位点的计算结果分析各个机位点 之间的差异,如表1所示。
从表中相同项目27 个机位点的结果中可以发现,各 机位点甘布尔分布拟合结果均比较好(大于0.99),不 同机位点之间存在一定差异。ECDs 阵风幅值最高的机位 点1达到13 m/s,而ECDs 阵风幅值最低的机位点27 为 9.8 m/s,二者相差3.2 m/s。一般的载荷计算会选址全 场包络最大值来代表整个风电场的载荷情况,因此对于 单个项目可以取最大的ECDs 阵风幅值来代表整个风电 场的阵风幅值情况,如表1中这个项目应该取ECDs 阵风幅值为13 m/s 的机位点1来代表该风电场的ECDs 阵 风幅值情况。
2.3 不同数据时长对ECDs 幅值结果的影响
由于本次分析是基于统计学上的方法进行的数据分 析,样本数的多少对分析结果存在一定的影响,对于风 电场SCADA 数据而言,样本数的多少直接取决于测风数 据的时长,为了尽可能消除小样本波动对分析结果的影 响,本次随机选择3个项目不同机位点,分别采用0.5 年、1 年、1.5 年和2年SCADA 数据进行处理,分析不 同测风时长情况下ECDs 阵风幅值的波动情况,其结果 如表2所示。从表中可以发现测风时长0.5 年和1年的 ECDs 阵风幅值结果存在较大差异,而数据时长超过一年 以后ECDs 阵风幅值相对比较稳定,因此在进行SCADA 数据分析时,需要选取数据时长一年以上的项目。
2.4 不同项目ECDs 阵风幅值结果分析
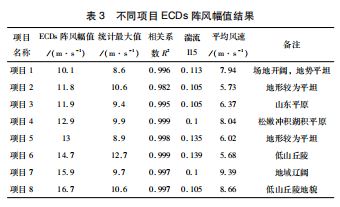
不同风电场项目所处位置、地形千差万别,即使均 是简单地形的项目不同项目之间风况条件也可能存在较 大差异,本文随机挑选了8个简单地形的项目,分析不 同项目之间ECDs 阵风幅值的差异,如表3所示。表中 ECDs 阵风幅值取的是各机位点中最大值,统计最大值为 对应实测数据中阵风最大值。从表中可以发现,不同项 目之间ECDs 阵风幅值差异较大,最小的项目1ECDs 阵 风幅值仅10.1 m/s,而最大的项目8ECDs 阵风幅值达到 16.7 m/s,二者相差6.6 m/s,因此对于定场址项目应该 采用场址本身的阵风幅值进行仿真,这样能较好地消除 标准模型的不确定性。从相关系数R2 可以得知这8个项 目拟合相关性较好,结合湍流强度和平均风速情况可以 发现,湍流强度和平均风速越低则项目ECDs 阵风幅值 越低,反之ECDs 阵风幅值越高。
3 结束语
综上所述,本文从IEC61400-1 标准提出的特定场址的 风向变化的极端相干阵风模型(ECDs ) 出发,基于风力发 电机组现场实测SCADA 数据,通过数据筛选和甘布尔函数 拟合分析最终得到各个风电场项目及其对应机位点的ECDs阵风幅值。通过对各结果分析得到的重要结论如下。
( 1 ) ECDs 阵风幅值对塔底合弯矩载荷影响较大,研究ECDs 阵风幅值具有较大意义;
(2 ) 通过甘布尔分布拟合累积概率的相关性良好,能较好地反映特定场址的ECDs 阵风幅值情况;
(3 ) 相同项目不同机位点之间ECDs 阵风幅值存在一定差异,应该采用整场最大的ECDs 阵风幅值作为该风电场幅值代表值;
(4 ) SCADA 数据时长对ECDs 阵风幅值存在一定影响,需要采用一年以上数据进行分析;
(5 ) 不同项目之间ECDs 阵风幅值存在较大差异,一般的湍流强度和平均风速越低则项目ECDs 阵风幅值 越低,反之ECDs 阵风幅值越高。
参考文献:
[ 1 ] 中国农机工业协会风力机械分会.风力机械标准汇编[M].北京:中国标准出版社,2006.
[ 2 ] Ahin A D.Progress and recent trends in wind energy [ J ].Progressin Energy and Combustion Science,2004.30 (5 ):501-543.
[3]李媛,毛竹.风力发电机组载荷计算中的极端风况分析[J].沈阳工业大学学报,2008.30 (4 ):409-413.
[ 4 ] IEC61400-1-2019 International standard,wind turbine generatorsystem,Edition 4-part1:Design requirements [ S ].
[ 5 ] Guidelines for design of wind turbines [ S ]. 2nd Edition,DNV&Risø,2002.
[ 6 ] Germanischer lloyd rules and guidelines industrial Services-2003.IV-Part 1:Guideline for the certification of wind turbines [ S ].
[ 7 ] Germanischer lloyd rules and guidelines industrial services-2010.IV-Part 1:Guideline for the certification of wind turbines [ S ].
[ 8 ] 中国船级社.风力发电机组规范[M]. 北京:人民交通出版社,2008.
[ 9 ] 吴治坚,叶枝全,沈辉副.新能源和可再生能源的利用[M ].北京:机械工业出版社,2006.
[ 10 ] Garrad Hassan & Partners. GH Bladed ( Version 4.3 ) TheoryManual [ Z ].2012.
[ 11 ] Garrad Hassan & Partners. GH Bladed ( Version 4. 3 ) UserManual [ Z ].2012.
[ 12 ] Hansen K S,Larsen G C.Full scale experimental analysis of extreme coherent gust with wind direction changes ( EOD )[ J ]. Journal of Physics Conference,2007 (75 ):012055.
关注SCI论文创作发表,寻求SCI论文修改润色、SCI论文代发表等服务支撑,请锁定SCI论文网!
文章出自SCI论文网转载请注明出处:https://www.lunwensci.com/ligonglunwen/63550.html