高考圆锥曲线解答题的研究方向论文

SCI论文（www.lunwensci.com）　　

　　摘要:圆锥曲线解答题是高考的重点考查内容，也是考查数学思想方法与核心素养的重要载体，对其进行分类研究有利于提升老师自身的解题素养，更有利于指导日常教学与高考备考．对通性通法的研究是最为重要的，是应对新情境下的圆锥曲线解答题的关键．

　　关键词:圆锥曲线;核心素养;数学思想;通性通法

　　2020年全国各地的高考圆锥曲线解答题考法多样，精彩纷呈，让人津津乐道．很多题目既有高等背景，又有常规易懂的通性通法．不同试题以数学思想方法为引领，又兼顾考查几大核心素养．有些题目源自往年经典考题，推陈出新，很好地考查了学生在新的情境下解决问题的能力．

　　1研究教材，适度延伸

　　很多高考题都是源于教材而又高于教材，所以“回归教材”必须成为我们备考复习的必经阶段，但是不应该成为一句空话，而是要实实在在地研究教材习题的解题思想并且适当地对题目进行变式延伸，帮助学生总结能够指导未来解题的“有效经验”．下面举例说明．

　　总结(1)以上三道题目都可以化归为“求点到直线的距离最值”问题，这是我们老师应该向学生总结梳理的．

　　(2)求椭圆上的点到直线的距离最值，可以设平行切线再求两线距离，也可以设椭圆参数方程用辅助角公式解决，这是对学生未来解题有帮助的“有效经验”，需要我们老师引导学生总结积累．

　　(3)三道题目都考查了数形结合的思想和直观想象的核心素养，启发我们要引导学生，主动借助图形性质去探索数学规律，解决数学问题．

　　(4)从历年的高考题中可以看到很多竞赛题的影子，竞赛题经过演变很可能成为以后的高考题，所以研究竞赛，找到高考与竞赛的结合点对我们的备考大有裨益．下面提供一个与前面三个例题有关的升级版供读者选用．

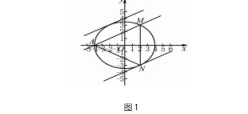
　　例4(2019年重庆高中数学联赛预赛第8题)△ABC为椭圆+=1的内接三角形，AB过点P(1，0)，则△ABC面积的最大值为．

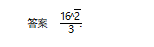
　　2研究算理，积累结论

　　数学运算素养是解析几何的核心素养，可以说“计算决定成败”，所以经常思考如何简化圆锥曲线中的复杂计算，可以帮助学生节省时间，准确作答，高效得分．根据《2017年版课程标准》对运算素养的描述，我们可以从运算对象、运算方法、运算程序等方面进行研究．

　　以直线和椭圆为例，设直线l:y=kx+m，椭圆

　　C:+=1，联立，消y，可得

　　(k2 a2+b2)x2+2a kmx2+a2 m2－a b22=0，

　　△=4a2 b2(k2 a2+b2－m2)．

　　由此可知，△的正负取决于k2 a2+b2－m2的符号．明白这一原理之后，可以为我们的解题带来极大的便利．比如前面的四道例题，都要用到直线和椭圆相切，于是利用k2 a2+b2－m2=0，这样便可以快速解方程或者找到未知数之间的联系．

　　再比如用“点差法”在处理“中点弦”问题时，比普通的联立、消y、用韦达的套路要简便得多，值得研究、积累、记忆结论．

　　总结通过研究点差法的运算原理可知，抛物线的弦所在直线的斜率只取决于p和弦中点的横坐标或者纵坐标．总结这一解题经验，可以为我们“预判”解题方向，简化计算，少走弯路．下面举例说明．

　　例5(2020年浙江卷21题节选)已知C1:+y2=1，C2:y2=2px(p＞0)，点A是椭圆C1与抛物线C2的交点，过点A的直线l交椭圆C1于点B，交抛物线C2于点M，点B，M不同于点A，若存在不过原点的直线l使点M为线段AB的中点，求p的最大值．

　　分析设A(x1，y1)，B(x2，y2)，M(x0，y0)，因为M 为线段 AB 的中点，所以首先想到使用结论 1 得

　　总结笔者看到此题的第一反应就是用结论1、结论2建立参数之间的联系，再逐步消元，留下目标p，再求解p的范围，于是轻松解决．但要跟学生强调，点差法的证明过程要在答卷上展示出来，避免直接使用结论而被扣分．

　　3研究高等背景，高屋建领

　　很多圆锥曲线题目有深厚的高等背景，如果能知道它们的来龙去脉，在教学的时候便可居高临下．如2020年全国Ⅰ卷理科20题与高等几何中的极点极线有关，下面先补充相关知识背景．

　　极点极线的几何定义如图2，过椭圆外一点P作椭圆的两条割线，分别交椭圆于A，B，C，D，连接AC，BD交于点E，连接DA，CB交于点F，则称直线EF为点P对应的极线．同理可知直线EP为点F对应的极线，直线PF为点E对应的极线．所以我们把△PEF叫做“自极三角形”．

　　去书写证明过程，会轻松明朗很多．(2)研究高等背景可以让我们登高望远，但是“研”与“教”是两回事，正如罗增儒教授所言:“解题研究无禁区，但解题教学有禁忌．”对于优等生可以适度扩展，渗透数学文化，但是对于基础一般的学生，还是以强化计算能力、掌握通法为主，所以我们研究的知识适不适合教给学生还得慎重考虑、因材施教．

　　4运用平面几何知识解题

　　全国卷历年的解析几何题目，经常可以使用平面几何知识处理，主要考查数形结合的思想和几何直观的核心素养，若从几何图形入手研究，发现图形与数量之间的规律，则可以实现“多一点想，少一点算”．

　　例7(2020年全国Ⅲ卷理科第20题节选)已

　　知椭圆C:+=1，A，B分别为C的左、右顶点，若点 P 在 C 上，点 Q 在直线 x = 6 上，且 | BP | = | BQ |，BP⊥BQ，求△APQ 的面积．

　　总结由已知条件容易想到初中常见的全等模型，用割补法求三角形面积省去繁杂的计算，由此可见，运用平面几何知识可以减轻计算负担，历年高考题，尤其是客观题，经常可以数形结合，找到图形规律再“秒杀”，值得我们深入研究．

　　5研究通性通法，以不变应万变

　　笔者把通性通法的研究放到本文最后才写，就是为了突出它的重要性，面对变化多端的圆锥曲线解答题，唯有通法是王道．下面笔者以前面的例6，即2020年全国Ⅰ卷理科第20题为例，回归基础，将解决此题的通性通法详细总结如下．

　　6.备考启发

　　以上详细分析的通性通法，可以迁移使用去解决2020年的山东卷和北京卷的圆锥曲线解答题，读者可以自行尝试．圆锥曲线题型多样，结论众多，而且高考经常创新问题情境，我们不可能让学生见过一切结论，也不可能依靠题海战术穷尽一切题型，唯一能做的就是不断总结处理圆锥曲线的通性通法，不断提升学生的运算求解素养，用有限的数学思想方法去应对无穷的题目，以不变应万变．

　　参考文献:

　　[1]中华人民共和国教育部．普通高中数学课程标准（2017年版)[M]．北京:人民教育出版社，2018．

关注SCI论文创作发表，寻求SCI论文修改润色、SCI论文代发表等服务支撑，请锁定SCI论文网！

文章出自SCI论文网转载请注明出处：https://www.lunwensci.com/ligonglunwen/63148.html