SCI论文(www.lunwensci.com)
摘 要: 文章结合一道平面图形翻折题的多视角、多方法解析,归纳解题规律,拓展解题思维,引领并指导解题研究.
关键词: 动点;翻折;轨迹;极端
立体几何是高中数学的主线之一,也是高考考 查的主干内容之一.近年高考对立体几何的考查,在 直观想象与创新意识等方面的要求较高,而平面 图形翻折成立体几何的问题,就是其中 一 种比较 吻合的考 点.对 于 这 类 平 面 图 形 的 翻 折 问 题,我 们要化“动”为“静”,“动”中取“静”,“动”“静” 结合,找到点 、直线 、平面等相关要素之间变与不 变的量,以 及 翻 折 过 程 中 关 键 点 的 变 化 轨 迹,合 理切入,巧妙应用.
1 问题呈现
问题 在 △ABC 中,已知 AB = 2BC = 4.AC =2倍的根号3,动 点 M 在 线 段 AC 上 ( 不 与 端 点 重 合),将 △ABM 沿直线 BM 翻折,使线段 AB 上存在一点 N, 满足 CN⊥平面 ABM,若 NB >λ 恒成立,则实数 λ 的最大值为 .
此题以一个直角三角形所对应的平面图形为问 题背景,结合线段上的动点与顶点所对应的直线进行翻折变化,构建相应的立体几何图形,利用另一线段中的存在点满足线面垂直关系来合理创设,进而 确定线段长度的变化情况,结合不等式恒成立引入 参数,巧妙确定参数的最值问题,内涵丰富,知识交 汇,形成一个“动”“静”结合、“定值”“最值”链接的 创新情境问题.
2 问题破解
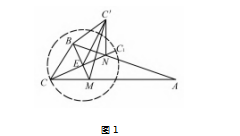
解法 1 ( 运动直观法) 由运动相对性,不妨固 定△ABM,将△BCM 绕 BM 翻折,作点 C 关于 BM 的 对称点 C1.连接 CC1.交 BM 点 E,则点 C 在翻折时 的轨迹为以E 为圆心,CE 为半径的圆.
由题意 CN ⊥平面 ABM,可知点 C 在底面 ABM 的投影点 N 在 CC1 上.
又点 N 在线段 AB 上,所以点 N 为线段 CC1 与 AB 的交点,当且仅当∠CBC1 ≥∠CBA 时满足题意.
如图 1 所示,当点 M 从点 C 移动到点 A 的变 化过程中,BN 的长度由大变小,所以当点 M 与点 A 重合时,此时 NBmin = 1 ( 因不含端点,故最小值 1 取不到).要使得 NB >λ 恒成立,则实数 λ 的最大值为 1.
解后反思 根据平面图形翻折的变化规律, 抓住“折痕”以 及 与“折 痕”垂 直 的 直 线,借 助 辅 助线的构建以及图形的对称性,可以巧妙直观地 确定相应翻折点的轨迹,以及直线与平面垂直条 件下的投影情况.
解后反思 根据平面图形的翻折变化,从角 的视角入 手,将 线 段 长 度 转 化 为 角 的 三 角 函 数, 利用三余弦定理是点睛之笔与沟通桥梁,巧妙地 将几个对应的三角函数值联系在 一 起,从而实现 变形与转化.
解法 3 ( 函数转化法) 如图 1 所示,设 CM = x,
解后反思 根据平面图形的翻折过程,在不同 平面内,引入线段长度的参数,利用解三角形思维, 借助勾股定理与余弦定理的应用,巧妙表示对应线 段长度的函数表达式,结合函数的单调性来确定对 应的最值问题.
解法 4 ( 四点向量定理法) 如图 1 所示,由 CN ⊥平面 ABM,可得 CN⊥BM.设 CM = x,结合四点向量定理,可得
解后反思 根据平面图形翻折前后的变化规律 确定平面上的四点,引入线段长度的参数,利用四点 向量定理合理构建对应的平面向量关系式,通过垂 直关系的确定,结合向量的模的转化来构建对应的 函数关系式,结合函数的单调性来确定对应的最值 问题.解法 5( 极端思维法) 根据 AB = 2BC = 4.AC =2倍的根号3.可知△ABC 是以∠C 为直角的直角三角形.
借助极端思维,易知要满足 CN ⊥平面 ABM,有 两个极限状态: 第一是 BM 为∠ABC 的角平分线时, 此时要满足条件,趋近于 BC 与 BA 重合,可得 NB→ 2; 第二是点 M 与点 A 重合( 或点 C 重合) 时,此时NB→ 1; 综上分析可知 NB ∈ ( 1.2),要使得 NB >λ 恒成立,则实数λ 的最大值为 1.
解后反思 根据平面图形翻折过程中的动态变 化规律,借助极端思维,从两个极端状态来特殊化分 析,进而以“静”促“动”,化“动”为“静”,利用极端 状态下对应的线段长度来确定线段长度的取值情 况,得以确定参数的最值问题.
3 变式拓展
平面图形翻折过程中,涉及点 、直线 、平面等 相关要 素 之 间 变 与 不 变 的 量,可 以 从 参 数 值 情 况 、位置关 系 判 断 、角 度 大 小 等 多 个 不 同 视 角 加 以变式与拓展.变式 1 ( 位置关系) 已知矩形 ABCD,AB = 2.BC =2倍的根号2.
将△ABD 沿矩形的对角线 BD 所在的直线 进行翻折,在翻折过程中( ).
A.存在某个位置,使得直线 BD 与直线 AC 垂直
B.存在某个位置,使得直线 AB 与直线 CD 垂直
C.存在某个位置,使得直线 BC 与直线 AD 垂直
D.对任意位置,三对直线“AC 与 BD”“CD 与 AB”“AD 与 BC”均不垂直
答案 B.
变式 2 ( 角度大小) 在菱形 ABCD 中,∠BAD=π/3.线段 AD,BD 的中点分别为 E,F.现将△ABD
沿对角线 BD 翻折,则异面直线 BE 与 CF 所成角的 取值范围是 .
答案 (π/3.π/2)
4 教学启示
4.1 抓住变化实质,挖掘运动轨迹
对于平面图形翻折成立体几何的问题,要分清 翻折前后图形的位置和数量关系的变与不变.一般 地,位于“折痕”同侧的点、线、面之间的位置和数量 关系不变,而位于“折痕”两侧的则会发生变化.
而在变化过程中,需要抓住关键点的轨迹,所谓 关键点是指翻折过程中变化的点,因为这些点的位 置变化会带动其他点、直线和平面的位置、数量关系 的变化.只有分析清楚关键点的准确位置,才能确定 其他点、线、面的关系,进而进行有关的推理、证明与 计算等.
4.2 总结解题规律,全面提升能力
破解平面图形翻折成立体几何的问题,其关 键是找准“动”与“静”的相对关系,瞄准“变”与 “不变”的确定关系,架起“平面”与“立体”的联 系桥梁,结 合 相 关 的 知 识 加 以 推 理 与 分 析.在 此 过程中,借助空间的转化,思维的跳跃,提升学生 的数学能 力,优 化 学 生 的 思 维 品 质,培 养 学 生 的数学核心素养.
参考文献:
[1] 冯成刚.立足教材平中出奇——— 对教材中一道立体几何练习题的探究 [J].高中数理化,2017 ( Z2) : 17 -18.
[2] 李建明.教材中一道立体几何问题的多视角探究 [J].中学数学,2018( 03) : 91-92.
[3] 孙鋆.一道立体几何试题的解法探究与拓展 [J].中学数学月刊,2017( 04) : 63-64.
关注SCI论文创作发表,寻求SCI论文修改润色、SCI论文代发表等服务支撑,请锁定SCI论文网!
文章出自SCI论文网转载请注明出处:https://www.lunwensci.com/ligonglunwen/63143.html