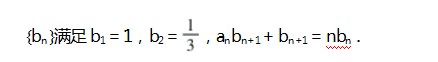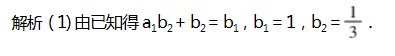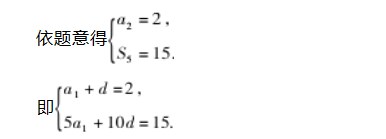SCI论文(www.lunwensci.com)
摘要:数列在高考中占有重要的地位,如何提高高考数列复习的实效性,本文总结了六种意识,提高学生的解题能力.
关键词:高考数列;解题意识;运算途径
1重视基本量解题意识
例1已知{an}是公差为3的等差数列,数列
(1)求数列{an}的通项公式;
(2)求数列{bn}的前n项和.
解得a1=2.
所以数列{an}是首项为2,公差为3的等差数列.
所以通项公式为an=3n-1.
(2)由(1)知an bn+1+bn+1=nbn.
点评在高考中,数列小题常考,通过基本量的关系求解,计算难度不大,但容易出错,个别题技巧性较强些.
例2已知等差数列{an}的前n项和为Sn,且a2=2,S5=15,求数列{an}的通项公式.
解析设等差数列{an}的公差为d.
解得a1=d=1.
所以an=n(n∈N*).
点评数列的基本量运算,特别是an与Sn的关系(易漏掉n=1时的情况)是高考的热点.
3合理选择运算途径意识
例3等比数列{an}的各项均为实数,其前n
点评高考数列考查等比数列,注意正确选择等比数列前n项和公式,而且要有整体消元的意识,从而可以快速计算.
4强化合情推理的训练意识
例4若a,b是函数f(x)=x2-px+q(p>0,q>0)的两个不同的零点,且a,b,-2进行适当排序后成等差数列,也可适当排序后成等比数列,则p+q的值等于.
解析由丰达定理得a+b=p,a·b=q.则a>0,b>0.
当a,b,-2适当排序后成等比数列时,-2必
综上所述,a+b=p=5.
所以p+q=9.
点评学生在解题过程中,恰当运用合情推理,会产生求证意识,从而提高解题能力.
5强化求和模型的训练意识
5.1裂项求和问题
例5已知数列{an}的通项公式为an=
点评注意裂项求和常适用于通项公式为分式的数列求和,特别是前面剩两项后面剩两项时,要分清剩哪两项.
5.2错位相减法问题
例6已知数列{an}的前n项和为Sn,且Sn=n(n+1)(n∈N*).
(1)求数列{an}的通项公式;
点评各项对齐后,注意错位相减后的运算准确性.
5.3集项求和问题
例7求数列{(-1)n·n2}的前n项和Sn.
解析(1)当n为偶数时,an-1+an=(-1)n-1·(n-1)2+(-1)n·n2=2n-1,
所以Sn=(a1+a2)+(a3+a4)+…+(an-1+an)=3+7+11+…+(2n-1)
点评在应用时应注意先求局部和,再求总和,往往适用于项的正、负符号不定的数列求和.
6关注数列的简单应用意识
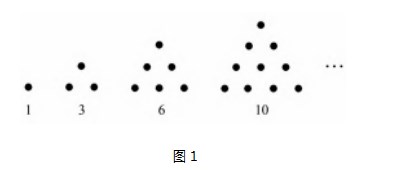
例8如图1所示的三角形数:
将三角形数1,3,6,10,…记为数列{an},将可被5整除的三角形数按从小到大的顺序组成一个新数列{bn}.可以推测:
(1)b2012是数列{an}中的第项;
(2)b2k-1=.(用k表示)
解析由题意可得an=1+2+3+…+n=
故b2012=b2×1006=a5×1006=a5030.
即b2012是数列{an}中的第5030项.
点评在具体实际问题中要有识别数列是哪一种数列的能力,关键是将实际问题如何转化.
参考文献:
[1]王中华.数列通项公式的求解策略[J].高中数理化,2019(07):12-14.
关注SCI论文创作发表,寻求SCI论文修改润色、SCI论文代发表等服务支撑,请锁定SCI论文网! 文章出自SCI论文网转载请注明出处:https://www.lunwensci.com/ligonglunwen/63104.html