SCI论文(www.lunwensci.com)
摘 要: 高中物理主要是培养学生的科学思维与动手实验能力,但是有些内容对数学运算能力 要求也比较高.高中物理课程标准明确指出“应用数学解决物理问题的能力”是物理教学的一项重 要要求,是考查学生能力的重要组成部分.利用数学方法解决物理中的极值问题是一类典型的物理 与数学相结合的题型,通过对此类题型的训练,对于培养学生创造性思维能力和掌握科学研究的方法均有重要的意义.
关键词: 极值,数学,二次函数,三角函数
1 利用二次函数求极值问题
1.1 利用一元二次函数判别式求极值
对于二次函数y=ax2+bx+c,用根的判别式法,利用 b2 -4ac≥0.( 式中含 y).若 y ≥A,则 ymin = A.若 y≤A,则 ymax = A.
例 1 汽车 A 以 v1 = 20m / s 速度匀速行驶,在 司机的正前方 100m 处有另一列汽车 B 正以 v2 = 10m/ s 速度匀速行驶,A 车立即做匀减速直线运动,加 速度为 a.为避免两车相撞,a 应满足的条件是什么?
1.2 利用配方法求极值
对于二次函数 y = ax2 + bx + c,函数解析式经配方 可变为 y = ( x-A) 2 + C,当 x =A 时,常数为极小值;
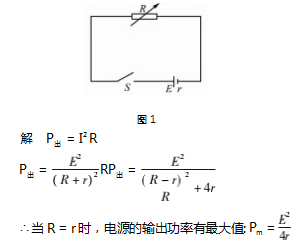
例 2 电路如图 1 所示,电阻 R 为可变电阻,电 动势为 E,内阻为 r 的电源,求 R 为何值时,电源的 输出功率有最大值? 最大值是多少?
2 利用基本不等式求极值问题
例 3 如图 2 所示,在水平地面上固定一个半 圆形光滑轨道,轨道直径与地面相垂直.一物块以速度 v 从轨道底端滑入,从轨道最高点飞出,物块落地点与 轨道下端的水平距离与轨道半径有关,当此距离最大 时,对应的轨道半径为多少( 重力加速度为 g) ( ).
例 4 有一山沟,一侧竖直,另一侧是呈抛物线 形状的坡面.有一人从山沟竖直一侧,以速度 v0 沿 水平方向跳到坡面上.如图 3 所示,以沟的最低点 O 为坐标原点建立平面直角坐标系.山沟竖直面的高
3 利用三角函数求极值问题
例 5 如图 4 所示
在斜上抛运动中,斜上抛物 体初速度为 v,与水平方向夹角为 α,在初速度一定 的情况下,为 α 多大时水平射程最大.
4 利用导数求极值问题
利用导数求物理极值可以拓宽学生的解题思路,让学生体会物理与数学的密切关系.应用导数方 法求极值的步骤如下:
4.1 根据物理问题所遵循的规律得出物理函数表 达式;
4.2 求函数的导数;
4.3 令 导 数 等 于 零,求 解 这 个 方 程,得 到 自变 量 的解;
4.4 判 断 出 该 解 对 应 的 是 极 大 值 点 还 是 极 小 值点;
4.5 把该解代入原方程求出对应的极值.
例 6 汽车 A 以 v1 = 20m / s 速度匀速行驶,在 司机的正前方 100m 处有另一列汽车 B 正以 v2 = 10m/ s 速度匀速行驶,A 车立即做匀减速直线运动,加 速度为 a.为避免两车相撞,a 应满足的条件是什么?
5 利用图像求极值问题
各种极值 问 题,还 可 以 利 用 函 数 图 像 、矢 量 图 、几何图 和 光 路 图 等 进 行 分 析 和 解 答. 图 像 法 和其他方法比较,不仅具有形象 、直观 、简捷和概 括力强的优点,而且对培养形象思维能力具有更 重要的意义.在利用函数图像求极值时,首先,应 根据各物理量的函数关系,在直角坐标系上画出 相应的函数图像,然后根据交点的坐标 、斜率 、截 距和与坐标轴包围的面积等的物理意义,进行分 析 、推理和计算.
例 7 如图 5.斜面倾角为 α,动摩擦因数为μ, 质量为 M 的小车沿斜面匀速向上运动,求拉力 F 与斜面夹角θ 是多少时,拉力有最小值?
高中物理中的求极值问题可以准确地考察学生 对物理知识理解的程度,培养学生数学运算能力.物 理学中的求极值问题属于知识性很强,涉及面非常 广的问题,在力学、热学、电磁学、光学中都有涉及, 笔者只是选择了几个代表性的问题进行分析.近年 来,高考加强了数学知识在物理中的运用,对学生数 学方法的掌握和运算能力提出了更高的要求,要求学 生能根据具体问题列出关系式并会进行相关推导和求 解,也重视定性和半定量的分析和推理.教师在平时的 教学中应根据不同的物理问题,一点一滴地把一些数 学方法渗透进去,使学生对物理规律的理解更加深刻, 使数学和物理这两门学科互相渗透、互相促进.
参考文献:
[1] 孙新科.高中物理极值问题的处理方法 [J].中学物理,2015.33( 23) : 96-97.
[2] 赵子怡.高中物理常见的极值问题解法探究 [J].科技创新导报 2016.12( 30) : 160 -161.
关注SCI论文创作发表,寻求SCI论文修改润色、SCI论文代发表等服务支撑,请锁定SCI论文网!
文章出自SCI论文网转载请注明出处:https://www.lunwensci.com/ligonglunwen/62957.html