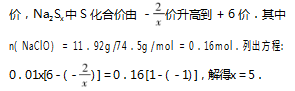SCI论文(www.lunwensci.com)
摘 要: 数学思想是数学学科的精髓,在解答其他学科习题中也有着广泛应用.高中化学解题 教学中,为使学生认识到数学思想的重要性,提高数学思想应用意识以及解题能力,应结合具体教 学内容做好相关习题的筛选,展示运用数学思想解题的过程,为学生以后运用数学思想更好的解答化学习题带来示范.
学生在数学思想指引下解答化学习题时更容易 找到解题思路,获得事半功倍的解题效果.其中方程 思想、数形结合思想、分类讨论思想、建模思想以及 极限思想时常应用.
1 方程思想
方程思想是一种重要的数学思想,即按照一定 的逻辑关系构建方程,将已知与未知参数建立联系 的一种思想,构建正确的方程是解题的关键.对于高 中化学学科而言,构建方程的依据为各种守恒思想, 如得失电子守恒、电荷守恒、原子守恒等,因此教学 实践中,教师应为学生做好这些守恒思想的深入解 读,使其把握守恒思想的精髓.
例 1 使用 11.92 g NaClO 配制溶液 100 mL,向 其中 加 入 0. 01 mol Na2 Sx 恰 好 完 全 反 应 生 成Na2 SO4 和 NaCl,则化学式 Na2 Sx 中 x 的值为 .
解答该题时,可根据题干描述列出对应的化学 方程式而后进行配平,可求出 x 的值.但是较为繁 琐,如运用氧化还原反应得失电子守恒这一规律,在 方程思想指引下列出对应的方程,可在短时间内求 出 x 的值.NaClO 中 Cl 的化合价由 + 1 价降低为 -1
2 数形结合思想
数形结合思想是高中数学解题中常用思想之 一.通过读图明确图像纵横坐标表示的含义,结合化 学反应掌握图线的变化规律,尤其注意图线的拐点、 交点等,不放过图线中的细节.
例 2 将 1mol HNO3 和 1mol H2 SO4 混合在一起后,逐渐向其中加入铁粉至过量.溶液中金属阳离 子 a、b 和加入铁粉的物质的量关系如图 1 所示,其 中稀硝酸的还原产物只有 NO,则以下说法错误的 是( ).
A.a 为 Fe3 + 的关系曲线
B.p 点时 Fe2 + 的物质的量为 0.6 mol
C.n1 的值为 0.75
D.在 p 点加入铜粉,最多可溶解 14.4 g
因存在2Fe3 + + Fe ═══3Fe2 + 这一转化关系且 铁是过量的,因此由图像可知先生成的为 Fe3 +,对 应曲线 a,Fe3 + 和 Fe 的反应对应曲线 b.两种酸混合 中 n( H + ) = 3mol,n ( NO3- ) = 1mol.由 Fe + 4H + + NO3- ═══Fe3 + + NO t + 2H2 O,可知 Fe3 + 达到最大 值时消耗 3mol H +,消耗 Fe、NO3 - 和生成 Fe3 + 的物 质的量均为 0.75mol.p 点 Fe3 + 和 Fe2 + 的物质的量 相等,设参加反应的 Fe3 + 物质的量为 xmol,则 有 0.75-x = 1. 5x,解 得 x = 0. 3.则 n ( Fe2 + ) = 0.45mol.在 p 点加入铜粉时发生反应 2Fe3 + + Cu = 2Fe2 + + Cu2 +,其中剩余的 n( Fe3 + ) = 0.45mol,则可 溶解 Cu 的物质的量为 0.225mol,对应 Cu 的质量为 0.225mol × 64g / mol = 14.4g.综上分析只有 B 项错误.
3 分类讨论思想
分类讨论思想是高中数学各类测试中常考的思 想.事实上在分析高中化学问题时,如果对情境、参 数、物质状态不能做出准确的判断,也需要进行分类 讨论.运用分类讨论思想解答高中化学习题与解答数学习题的步骤基本一致,即根据题意确定分类讨 论的依据,按照一定顺序或逻辑关系进行分析.
例 3 如图 2 所示的两个容器,在保持其他条 件相同的情况下,将 2mol X + 2mol Y 分别加入到两 个容器中.若开始时两容器的体积均为 V L,发生以 下反应: 2X + Y ⥫⥬aZ( g),其中 X、Y 的状态未知. 若此时 Ⅰ 中 X、Y、Z 的物质的量之比为 1∶ 3 ∶ 2.则以 下说法中一定正确的是( ).
A.若 X、Y 均为气体,平衡时气体平均摩尔质 量: Ⅱ> Ⅰ
B.若 X、Y 不均为气体,则平衡时气体平均摩尔 质量: Ⅰ> Ⅱ
C.若 X 为固态,Y 为气态,则 Ⅰ、Ⅱ从起始到平 衡所需时间相同
D.平衡时 Ⅰ 的体积不足 V L
该题考查学生对平衡移动知识的理解以及灵活 运用情况.因 X、Y 的状态未知,因此,需要运用分类 讨论思想进行分析.根据题干设 Y 参加反应的物质 的量为 n 列出三行式,结合 X、Y、Z 的物质的量之比 为 1 ∶ 3∶ 2 可求出 a 的值为 1.当 X、Y 均为气体时 Ⅰ 和Ⅱ相比, Ⅰ 相当于加压平衡正向移动,气体物 质 的量变小,对应的平均摩尔质量增大,即 Ⅰ > Ⅱ. 若 X、Y 不均为气体且 Y 为气体时,压强对化学平 衡无影响,两 容 器 的 气 体 平 均 摩 尔 质 量 相 等.此 时两容器处于等效平衡状态,从起始到平衡经历 相同时间且平衡时 Ⅰ 的体积仍为 V L.综上分析 一定正确的是 C 项.
4 建模思想
建模思想是基于对问题本质的抽象理解,运用 数学语言予以概括、表征的一种思想.高中化学涉及 很多模型,如氧化还原反应模型、化学平衡模型、电化学模型等.这些模型是高中化学的重点,是各类测 试的热门考点.
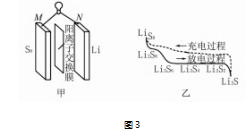
例 4 一种锂流电池的总反应为 16Li + S8 ═══ 8Li2 S.该电池的装置如图 3 甲所示,充电和放电过 程如图 3 乙所示,则该电池工作时以下说法不正确 的是( ).
A.放电时,M 电极的电势高于 N 电极
B.放电时,Li + 通过阳离子交换膜到达 M 电极 附近
C.充电时,M 电极反应式为 8Li2 S -16e - ═══ S8 + 16Li +
D.充电时,1 mol Li2 S4 转化为 Li2 S6 电路中通过 2mol 电子
该题考查原电池以及电解池知识.要想迅速解 答该题需要在头脑中建立清晰的原电池和电解池模 型,搞清楚原电池和电解池原理、对应的电极名称、 对应电极上发生的反应类型.由图 3 乙可知放电时 Li 失去电子化合价升高,则 N 为负极,M 为正极,M 极电势高于 N 极. 阳离子会向 M 极移动,结合图 3 甲可知 Li + 通过阳离子交换膜.充电时由电解池模 型可知 M 电极为阳极,N 电极为阴极,结合放电时 正极总反应式,不难推出充电时 M 电极反应式为 8Li2 S -16e -═══S8 + 16Li +.充电时阳极反应式为 3Li2 S4 -2e - ═══2Li2 S6 + 2Li,1 mol Li2 S4 转 化 为
5 极限思想
极限思维是用极限概念分析问题和解决问题的一种数学思想.极限思想在高中化学学习中有着广 泛的应用,尤其在分析混合物的组成、化学平衡、物 质参数取值范围问题中时常运用到极限思想.
例 5 向 100 mL 0.1mol / L 的 Fe2 ( SO4 ) 3 溶液 中通入标准状况下为a L 的 SO2 与 Cl2 的混合气体, 充分反应后溶液棕黄色变浅.而后向反应后的溶液中 加入足量 BaCl2 溶液,过滤、洗涤、干燥后称量得到的沉淀,质量为 11.65 g,则 a 的取值范围为 .
0.02mol则参加反应的 SO2 、Cl2 的物质的量均为0.02 mol,对应标准状况下的体积为0.04 × 22.4 L/ mol = 0.896 L; 若 Cl2 的含量非常少,溶液中 0.01 mol 的 Fe3 + 全部参加反应,①②两个反应均发生,由②可知消 耗 SO2 和生成 SO4(2) - 的物质的量均为0.01 mol.则① 中生成 SO4(2) - 的物质的量也为0.01 mol,消耗 SO2 、 Cl2 的物质的量均为 0.01 mol.则 SO2 和 Cl2 的总的物 质的量为0.03 mol,对应标准状况下的体积为0.672 L.
综上分析a 的取值范围为0.672 L<a<0.896L
参考文献:
[1] 张乾丰,刘玉荣,来俊军.数学极限思想在高中化学教学中的应用 [J].化学教学,2021( 05) :85-90.
[2] 刘宇.数学思想与原理在化学试题解答中的使用 [J].数理化解题研究,2019( 22) : 93-95.
关注SCI论文创作发表,寻求SCI论文修改润色、SCI论文代发表等服务支撑,请锁定SCI论文网!
文章出自SCI论文网转载请注明出处:https://www.lunwensci.com/ligonglunwen/62941.html