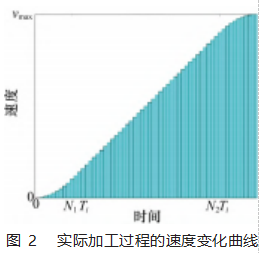
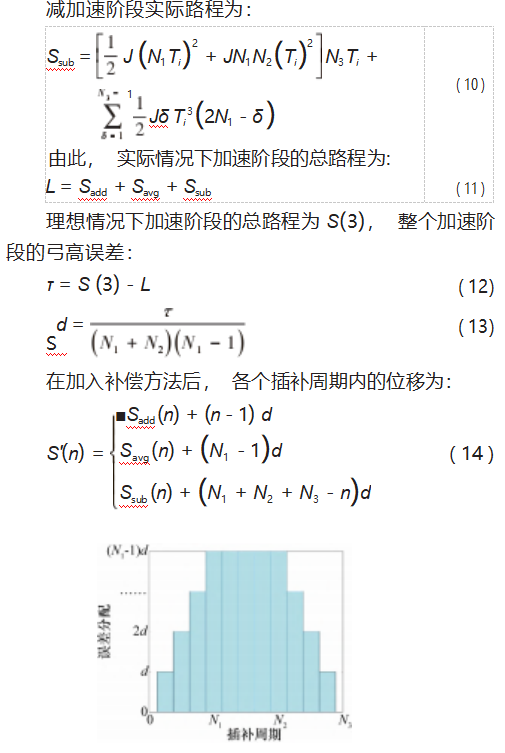
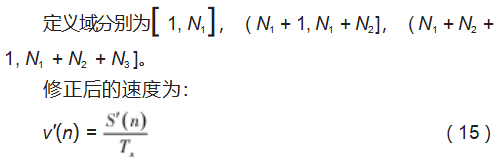假设数控系统的插补周期为Ti,加加速阶段的时间为Tadd,插补周期个数为N1;匀加速阶段的时间为Tavg,插补周期个数为N2;减加速阶段的时间为Tsub,插补周期个数为N3,则有:
由此可得每个插补周期内误差修正后的速度,保证了速度规划的轨迹与实际插补轨迹相同,使得速度变化过程更为平滑,同时消除了误差,提升了加工精度。
3 MATLAB仿真
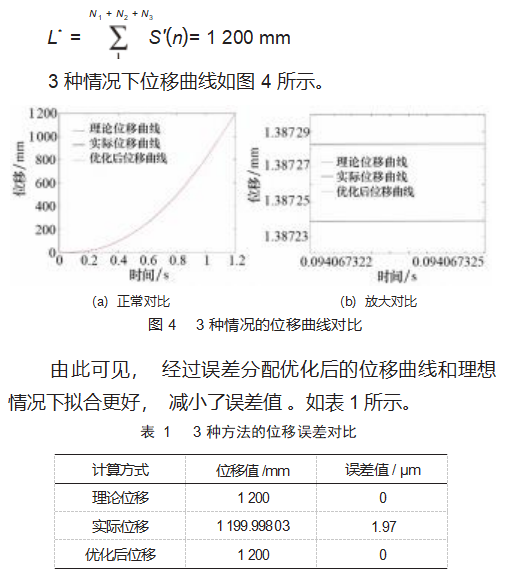
设加加速度为J=10 000 mm/s3,最大加速度为a=2 000 mm/s2,最大速度为v=2 000 mm/s。
4结束语
本文对数控系统S型加减速进行了深入研究,基于7段S型加减速控制算法,介绍了S型加减速算法的原理,再通过数学计算重点介绍分析S型加减速过程中误差产生的原因,在此基础上提出误差分配思想,优化后的加减速算法可以解决插补过程中产生的弓高误差,还能够在一定程度上克服速度变化不连续的问题。最后通过MATLAB对理想情况下进行仿真测试,结果表明,在其他条件相同的情况下,加入误差补偿优化的效果优于其他传统S型加减速方法,能够实现速度间的平滑过渡,有效减小运动过程产生的弓高误差值,保证了加工的稳定性与加工精度,且算法复杂度较低,对分析机床加减速性能的研究有一定的参考价值。
参考文献:
[1]司慧晓.数控加工中加减速控制及平滑算法的研究与实现[D].沈阳:中国科学院大学(中国科学院沈阳计算技术研究所),2017.
[2]吴继春.曲面数控加工编程轨迹的NURBS拟合及插补算法研究[D].武汉:华中科技大学,2012.
[3]赵巍.数控系统的插补算法及加减速控制方法研究[D].天津:天津大学,2004.
[4]张丹凤.数控系统插补算法研究及设计[D].沈阳:东北大学,2009.
[5]叶荫民.数控系统的加减速控制算法及其实现[D].兰州:兰州交通大学,2019.
[6]朱长峰.连续微线段高速加工数控系统路径与速度前瞻规划算法研究[D].杭州:浙江大学,2018.
[7]陈铮杰.嵌入式数控系统微小线段平滑插补算法研究[D].南京:南京航空航天大学,2014.
[8]商允舜.CNC数控系统加减速控制方法研究与实现[D].杭州:浙江大学,2006.
[9]谢暴.数控系统插补算法的优化设计[J].华夏星火,2005(9):70-72.
[10]杨召彬,王宏甲,乔磊,等.基于差分插补原理的数控系统加减速规划[J].机床与液压,2019,47(8):157-160.
[11]许海峰,王宇晗,李宇昊,等.小线段高速加工的速度模型研究和实现[J].机械工程师,2005(4):9-13.
[12]李建刚,吴响亮,李泽湘,等.连续加工路径的进给速度规划算法研究[J].哈尔滨工业大学学报,2009,41(3):29-32.
[13]游有鹏,张礼兵,何均.高速高精度数控系统若干控制技术的原理分析和应用进展[J].航空制造技术,2010(11):60-63.
[14]赵翔宇,蔡慧林.三次S曲线加减速算法研究[J].机械科学与技术,2016,35(5):747-751.
[15]潘敏,邬义杰,冷洪滨.数控系统加减速控制方法的研究[J].制造业自动化,2005,27(9):4.
[16]石川,赵彤,叶佩青,等.数控系统S曲线加减速规划研究[J].中国机械工程,2007,18(12):5.
[17]谢剑云.数控系统加减速控制方法研究现状[J].机械管理开发,2009,24(5):2.
[18]李峰.一种实用的数控系统加减速控制方法[J].现代制造工程,2004(5):2.