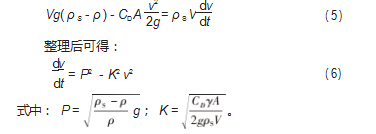SCI论文(www.lunwensci.com)
摘要 :在一些风大浪急的海域进行临时机场的铺设施工作业时传统的打桩填满方式较为复杂和困难 。为此提出了一种基于大型六 面十二边刚性透水框架的水上临时跑道的铺设方法, 其关键是要详细了解环境因素对刚性框架下落过程的影响 。为研究水深和海 流形式对大型六面十二边透水框架下落过程的影响, 设计了一种大型的六面十二边透水刚性框架, 并提出了该类型框架下落过程 的计算理论 。结合某海域具体海况, 通过对框架下落过程的必要简化, 结合凝集 6D浮标和 Link 单元, 运用大型水动力分析软件 OrcaFlex 建立了大型六面十二边透水框架下落过程的动力学分析模型 。运用时域耦合分析得到了该六面十二边透水框架的下降速 度 、六自由度 、空间轨迹等的变化情况, 计算结果对具体工程实践有一定的指导意义。
关键词:大型六面十二边透水刚性框架,OrcaFlex,动力学分析,下落过程
Dynamics Analysis of Falling Process of Large Rigid Permeable Frame of Hexahedron with Twelve Sides Under Different Water Depths and Current Patterns
Zhang Dapeng1※, Zhao Bowen2. Zhu Keqiang3
( 1. Ship and Maritime College, Guangdong Ocean University, Zhanjiang, Guangdong 524088. China; 2. Ocean College of Zhejiang University,
Hangzhou, Zhejiang 316021. China; 3. Faculty of Maritime and Transportation, Ningbo University, Ningbo, Zhejiang 315211. China)
Abstract: The traditional pile driving and filling method is complex and difficult when paving facilities at temporary airports in some windy
and turbulent waters. A laying method for a temporary runway on water based on a large hexahedron 12-side rigid permeable frame is
proposed, and the key is to grasp the influence of environmental factors on the falling process of rigid frame . In order to study the influence of
water depth and current patterns on the falling process of large hexahedron 12-side rigid permeable frame, a large hexahedron 12-side
permeable rigid frame was designed, and a theory of computation for the falling process of this type of frame was proposed . Based on the
specific sea conditions of a certain sea area, a dynamic analysis model for the falling process of a large hexahedron 12-side permeable frame
was established with the large hydrodynamic analysis software OrcaFlex by simplifying the falling process of the frame , combining the lumped
6D buoy and Link unit. The time domain coupling analysis is used to obtain the descending velocities, six degrees of freedom, spatial trajectory
and other changes of the hexahedron 12-side permeable frame. The calculation results have certain guiding significance for specific
engineering practice.The falling velocities, six degrees of freedom, spatial trajectory of the rigid frame are obtained by time-domain coupling analysis. The calculation results have certain guiding significance for actual engineering practice .
Key words: large hexahedron 12-side permeable frame; OrcaFlex; dynamic analysis; falling process
引言
在南海一些有争议性的海域, 如果动辄出动航空母舰, 难免会带来政治和军事层面上的被动[ 1] 。另一方面, 在一些水域面积宽广 、流速较大 、水深较深 、风大浪急、 海床平坦的海域, 如果进行一些非永久性的海上作业操 作, 如铺设临时海上起降机场等, 是没有必要在海底进 行打桩作业的 。一方面, 在这样的水域进行海底打桩作 业其施工成本较大 、技术难度较高, 另一方面也无法保 证施工过程中的安全[2-8]。
针 对 这 种 情 况, 结 合 张 召 忠 老 师 曾 经 提 出 的 建 议[9- 10], 本文认为可以考虑在这些海域投放若干大型的 刚性六面十二边透水框架, 将这些刚性透水框架按照一 定的排列布局布放在海底, 然后结合一些系泊缆索将其 系固在海床上辅以合适的配重和浮筒, 通过调节其浮力 大小和系泊缆索的长短, 实现刚性边框群在海面高度的 升降 。然后再在这些边框群的水上表面铺设上相应的跑 道材料, 就可成为简易的临时水上起降机场 。该方法能 够大大降低施工的成本和难度, 且对于一些时间上要求较为紧急的应急性军事任务有着很强的军事价值和战略 意义, 对于我国实现在南海海域的一些远离大陆的水域 的现实存在与控制也有着十分重要的意义。
纵观国内外文献, 文献[9]提出了大型刚性框架在海 洋军事斗争中应用的命题, 文献[10]结合航母的运维成 本指出了大型框架在建造海上机场方面的经济和技术方 面的优越性 。文献[11- 16]对各类海洋浮体的性能与应用 展开了不同研究, 但均未涉及大型框架的海洋布放策略 及技术分析 。 目前尚无大型刚性框架下水过程的相关研究。
针对这种情况, 考虑到六面十二边框架比四面六边 框架更容易进行海上施工布放的特点, 本文提出了大型 六面十二边透水刚性框架这一设想 。并通过大型水动力 分析软件 OrcaFlex 对该框架的下水过程进行了仿真 。仿 真中发现水深与海流的形式对于这种大型框架的布放与 空间轨迹有着非常显著的影响 。如掌握了某一海域的具 体海况, 就可以根据实际情况选择最佳布放策略在该海 域布放由多个该大型六面十二边透水刚性框架组成的阵 列, 进而达成我们的工程目的或是军事目的。
1 六面十二边透水框架的落水过程
1.1 初始入水速度
假设该六面十二边透水框架被海洋起重船吊起, 然 后在距离海面高度 H处框架被起重船释放, 开始做自由下落运动, 忽略其受到的空气阻力, 设其初始距离海平 面高度为 H, 则在入水的瞬间其速度为:
1v0 = ( 2Hg) 2 ( 1 )
式中: v0 为框架入水时的初始速度; g 为重力加速度。
大型的框架在与水面接触的瞬间由于要穿过海面, 因此会受到海水对它的抨击力作用, 海面与框架相互作 用产生的瞬间抨击力属于急剧的冲击载荷, 会让框架的 速度瞬间减小, 设框架减小后的速度为 v 0(1)。
瞬间的抨击力在本文中通过参考 DNV 规范对框架的 入水抨击力系数的选取予以考虑。
1.2 框架入水后的垂直方向受力分析
六面十二边透水框架入水后的等效重力可表示为:
W = Vg ( ρ S - ρ ) ( 2 )
式中: V 为透水框架的等效真实排水体积; ρs 和ρ 分别为 框架杆件的密度和海水密度。
框架下落过程中受到的水流的垂直阻力为:
F = CD Aγ
( 3 )
式中: CD 为透水框架的绕流阻力系数; A 为透水框架下 落过程中在垂直方向实际对水投影的面积; v 为透水框 架在水中的瞬时速度; γ 为水的重度。
在竖直方向对透水框架进行水中的受力分析, 有:
W - F = ma ( 4 )
式中: m=ρs V, 为透水框架的质量; a=dv/dt, 为透水框架 在 水 中 下 落 的 垂 直 加 速 度 。将 式 ( 2 ) ~ ( 3 ) 代 入 式 ( 4 ) 可得:
当透水框架匀速下沉时, 加速度 a=0. 即 dv/dt=0. 此时的垂直方向的沉降匀速记为 v ∞, 代入式 ( 6 ) 可得:
1.3 框架入水后的水平方向受力分析
忽略海风的作用, 透水框架入水后在水平方向受到的力只有水流对框架的作用力, 根据牛顿第二运动定律 可得:的力只有水流对框架的作用力, 根据牛顿第二运动定律 可得:
式中: CDL 为水平方向水流作用系数; AL 为透水框架水平 方向的投影面积; U为水流流速 (这里水流流速可以为 水深的函数, 也可以为流向角的函数); vL 为透水框架水 平方向的瞬时速度。
将边界条件代入式 ( 15 ), 积分可得透水框架的水平 运动速度:
2 框架落水过程的动力学仿真模型
实际海上操作时, 大型框架被海上起重船起吊至海 平面某一高度, 然后释放让其以自由落体形式落入海水 中 。在仿真建模时, 为简化建模过程增强模型的收敛性, 调用了 OrcaFlex 中的 Link 模块 。Link 模块在建模仿真的 过程中一般有弹簧阻尼器和释放开关两个作用 。在建模 初始时刻, 通过 Link 单元将 6D 凝集质量块模拟的大型六 面十二边透水框架水平固定在海平面某一高度处, 静平 衡阶段结束后, 将 6D 凝集质量块在动态阶段释放 。为了 节省计算时间, 静平衡阶段设置为 5 s。
仿真中将六面十二边刚性透水框架设为边长为 10 m 的正方体边框以做定量的分析, 该边长可以满足大部分的 海上施工要求。考虑到工程实践中钢架的海上运输问题和 在某一海域将单根钢结构组装成框架的难易程度, 实际海 上施工时要依据具体海况和需求来选择刚性边框杆件的边 长和截面大小。并且考虑到钢材的质量较大, 因此边框的 边长不易过长, 过长的边框会由于其自身的重力作用发生 一定程度的弯曲, 这样难以保证组装以后框架整体的刚性。
6D 凝集质量块创建的刚性透水框架的边框为纯刚性, 不会发生变形, 因此仿真中运用 6D 凝集质量块来模 拟该六面十二边刚性透水框架 。工程中, 边框杆件的材 质和截面属性影响着框架的刚性, 仿真建模在一定程度 上简化了边框杆件的截面形式对仿真结果的影响 。此外, 边框杆件的截面还影响透水框架入水后水流对于框架的 作用力的大小 。仿真时可以通过赋予 6D 凝集质量块同一 水流作用方向下不同的拖曳力系数和拖曳面积来体现 。
不同水流作用方向的水流拖曳力系数也是不同的, 仿真 中, 主要涉及水平和竖直两个方向的拖曳力系数 。刚性 框架的质量为 381.02 t, 水流拖曳总面积为 38.4 m2. 水 平方向的拖曳力系数为 0.85. 垂直方向的拖曳力系数为 1.7. 转动惯量为 Ix=Iy=Iz= 12 700.7 t ·m2. 根据 DNV 规范, 框架的入水抨击力系数取为 5[ 17]。
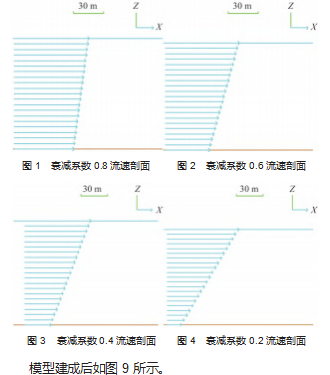
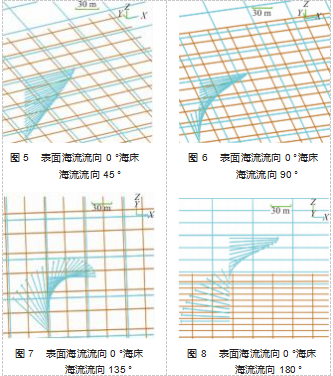
为探究不同水深对于六面十二边透水刚性框架落水 过程的影响, 这里取 50 、100 、150 、200 m 五种不同水 深, 此时的水流流速统一设定为 1 m/s, 流向均为 0 °; 为探究不同海流流速的影响, 在保持流速不随着水深而 变化 、流向均为 0 ° 、水深为 100 m 的前提下, 海流流速 设置为 0 、2 、4 、6 、8 、10 m/s; 由于海水的黏性作用, 随着水深的递增, 海流流速越小, 为探究不同形式海流 对该大型刚性框架的影响, 设海流随着水深的递增线性 递减, 海底的海流流速为表面海流流速与海流衰减系数 的乘积, 海流衰减系数越小, 海流在海床的流速越小, 分别选择海流衰减系数分别为 0.8 、0.6 、0.4 、0.2 、0. 在表面海流均为 5 m/s, 流向为 0 °, 水深为 100 m 时进行 动态仿真, 如图 1~4 所示; 为探究随着水深的变化流向 线性的变化对刚性框架下落过程的影响, 此时水深均设 为 100 m, 流速不随水深递增而衰减, 流速均为 10 m/s, 设在海平面流速方向为 0 °, 在海底流速方向分别为 45 ° 、90 ° 、135 ° 、180 °, 如图 5~8 所示。
3 计算结果
3.1 水深对框架下放入水过程的影响
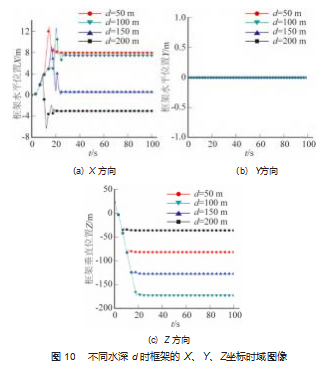
不同水深时框架的X、Y、Z坐标时域图像如图10所示。
观察图 10 (a) 可以发现: 在流速和流向保持不变 的情况下, 框架在落到海底上之前在水平 X 轴正方向的外飘距离随水深的增加而增加; 框架在落到海床上的瞬 间达到其在 X 轴正向的最大位移, 此后由于框架的翻滚 作用导致不同深度下框架都会沿着 X 轴的负方向迅速衰 减到一个与该深度所对应的特定的稳定值不再发生变化; 在水深为 50 m 时, 虽然流向为 0 ° (与 X 轴正向相同), 但由于此时在框架与海床接触的瞬间框架发生的沿 X 轴 负向的翻滚导致的负向位移大于框架在海流作用下发生 的 X 轴正向的位移, 因此在框架稳定停在海床上以后框 架在 X 轴上的位置反而发生了较初始位置时刻的负向位 移; 也就是说, 在海流与 X 轴在同一直线方向时, 当水 深较浅时框架最终在海床上 X 轴方向的偏移位置有可能 与流向相反而不是相同, 这告诉我们当在浅水进行框架 下落布放时要预防与来流方向相反的 X 轴位移的发生。
观察图 10 (b) 可以发现, 不同水深作用下框架在 Y 方向上的位移高度重合, 这说明在流向为 0 °时, 水深的 改变对框架 Y方向上的位移几乎没有影响。
观察图 10 (c) 可以发现, 在框架落到海床上前框 架的 Z方向的时域曲线高度重合, 这说明在框架落到海 床上前水深对框架在 Z 方向的位置变化无影响, 水深主 要影响的是框架落到海床上的时间, 水深越深, 框架落 到海床上所需要的时间越长。
虽然总的动仿真时间为 100 s, 但事实上不同水深下 框架在 30 s 左右其平动速度已经为 0. 为便于数据的观 测, 在速度- 时间图像中采集到静平衡阶段到动态仿真 阶段的第 35 s 即可。
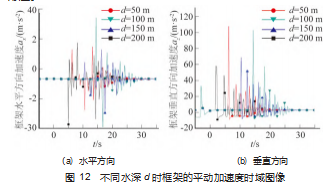
不同水深时框架的平动速度时域图像如图 11 所示。在流向为 0 °时, 观察图 11 (a) 不同水深条件下框 架在 X 轴方向的速度分量 Vx 的时域图像发现: 不同水深条件下框架在 X 方向的速度分量在时域上都会发生沿 X 轴正负方向的反复变化, 且这种速度方向的波动主要集 中在框架与海床接触瞬间到框架停止运动这一段时间内; 虽然框架在 X 轴的速度运动方向会反复波动, 但结合其 在 X 方向的位置图像可知, 只有在水深较浅时其位移才 会偏离其初始位置的负向, 总体而言, 框架最终稳定时 还是沿 X 轴正方向外飘 。而且框架的最大 X 轴正向速度 并不是出现在水深最深的情况下, 这说明随着水深的增 加虽然框架在水流中受到的冲击作用时间变长, 但由于 海床的作用, 在框架落到海床上以后, 海床对框架的作 用还是会对框架的最大 Vx 正向速度的大小产生不可预测 的影响。
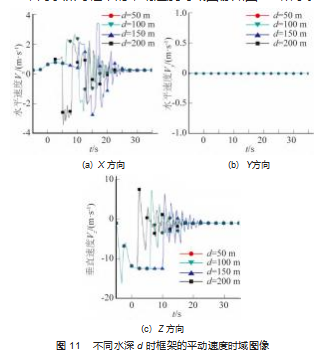
在流向为 0 °时, 水深的变化对框架在 Y轴方向上的 Vy 速度几乎无影响, 这与不同水深条件下框架在 Y 方向 的位置时域图像得出的结论基本一致 。在流向为 0 °时, 观察图 11 (c) 框架的 Vz 图像发现不同水深时在入水前 框架的垂直方向速度的变化情况一致, 而在框架入水的 瞬间, 由于抨击力的作用, 框架会迅速沿 Z轴正向短时 间内大幅度减速, 但其在这一减速过程中的速度方向始 终沿 Z轴负方向, 速度并未减少到 0; 当抨击力的作用消 失后, 框架在重力和浮力合力的作用下继续做沿 Z 轴负 方向的加速运动, 在与海床接触的瞬间沿 Z 轴垂直向下 的 Vz 速度达到最大; 在与海床接触后的下一个瞬间, 由 于海床对框架持续而急剧的向上作用力使得框架在此刻 立即改变了 Vz 的速度方向, 并达到沿 Z轴正向方向上的 速度最大值; 最终框架的 Vz 速度逐渐衰减为 0 。总结可 得, 对框架沿 Z 轴垂直向上的 Vz 速度数值大小影响最大 的是框架在掉落海床瞬间与海床的相互碰撞作用, 而不 是水深的变化 。当然, 水深的变化对框架的垂直速度的 变化也有着不可忽视的影响, 但如果水深足够深, 由于 水的黏性和阻尼作用, 框架最终会在垂直方向达到受力 平衡, 这时再改变水深, 框架的垂直下落的速度将不再 发生变化 。也就是说, 在框架下落的过程中, 应该存在 临界水深, 使得框架在垂直方向恰好受力平衡 。因此在 未达到临界水深前, 水深的变化和海床与框架的相互作 用都会对框架的最大正向垂向速度 Vz 产生影响, 而如果 达到这一临界水深, 影响框架最大正向垂向速度 Vz 的会 是框架与海床在接触瞬间的碰撞作用, 影响这一碰撞作 用的主要因素与海床的地形类型 (平坦海床 、倾斜海床) 以及海床的土力学性能有关。
由于框架在 Y方向的位移和速度都几乎为 0. 因此其 在 Y方向上的加速度也几乎为 0. 故这里不再画出框架在 Y方向上的加速度 。观察图 12 可以发现: 框架垂直方向 的最大加速度的数值远远大于水平方向的最大加速度的 数值, 水平方向的加速度图像除了大小有所不同以外,其在时域上的分布形态大体相同; 且其最大的垂向加速 度方向都是垂直向上的, 且随着水深的增加, 垂直向上 最大加速度出现的时刻由刚入水的瞬间逐渐向与海床接 触的瞬间转移, 在达到某一水深后该时刻又回到刚入水 的瞬间, 这再次说明了前面关于“临界水深”存在的正 确性。
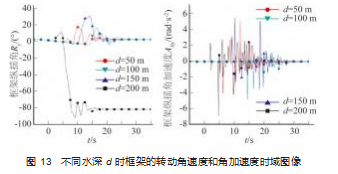
仿真时发现当流向保持 0 °不变不同水深时框架的横 摇角和艏摇角在下落过程始终为 0. 故这里不再画出, 其对应的横摇角加速度和艏摇角加速度也不再画出。
通过仿真发现, 框架的转动主要集中在纵摇方向 。 观察不同水深时框架的纵摇角在时域上的分布情况发现, 在水深较浅时 ( 50 m), 框架在入水的瞬间发生一个小幅 度的正向纵摇, 框架入水后快速发生负向的纵摇, 最终 保持在负向纵摇角 90 °停在海床上; 而在水深较深时, 框架入水后先发生正向的纵摇, 在与海床接触的瞬间又 再次慢慢回到 0 ° 。框架的纵摇角加速度表明不同水深条 件下框架的纵摇角都会经历先正向纵摇加速然后负向纵 摇减速, 最终纵摇加速度在这两个方向反复波动逐渐减 小为 0. 且产生角加速度的阶段主要集中在与海床接触 瞬间到框架最终停止在海床上这一阶段 。在水流流向始 终为 0 °且流速大小不沿着水深衰减时, 如无海床与框 架的相互作用, 单一水流的冲击作用并不会使框架发生 转动。
3.2 海流流速对框架的下放入水过程的影响
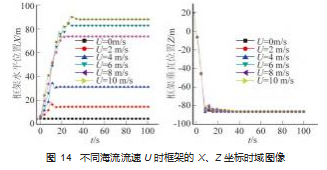
在保持海流方向不变的情况下, 可以看出不同海流 流速下框架水平 X 轴方向的外飘距离是不同的, 且随着 流速的增加而不断增加 。观察图 14 (b) 可知, 不同流速下框架在垂直方向的下落轨迹高度重合, 说明流速的 变化对框架在垂直方向的下落运动几乎无影响。
仿真发现, 在 0 °流向时, 不同流速下框架 Y方向的 位移 、速度与加速度几乎均为 0. 且在 Y方向的位移在落 到海床上之前为 0. 在框架落到海床后与海床发生碰撞 导致翻滚, 才会使框架在 Y 方向产生非常微小的位移, 其数量级为 10- 15 m, 几乎可以忽略, 故这里不再画出 Y 方向的相关平动图像 。也就是说, 在海流流向为 0 °时, 框架在水平方向的位移主要集中在 X 方向, 这告诉我们, 当流向方向为 0 °或 180 °时, 框架的水平方向的位移主 要集中在此时与流向在同一直线方向的 X 方向; 同理, 如果流向方向为 90 °或 270 °时, 框架的水平方向的位移 主要集中在此时与流向在同一直线方向的 Y方向。
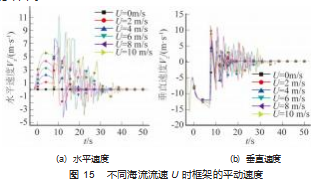
虽然动态仿真的总时间为 100 s, 但不同流速下框架 在 45 s 左右其平动速度已经为 0. 为便于数据的采集和 观测, 图 15 仅给出前 50 s 的静平衡阶段到动态仿真阶段 的结果。
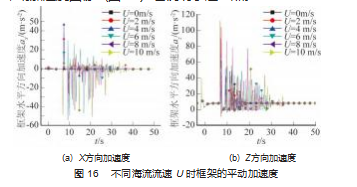
观察图 15 可以发现, 框架在入水前的平动速度主要 集中在 Z方向, 这是由于这一阶段框架在做重力作用下 的自由落体运动造成的; 在框架入水后, 框架的平动速 度主要集中在 Z 方向和 X 方向; 由于水流的阻尼作用和 巨大的入水抨击力, 框架在 Z方向做先减速后减速到一 定速度后再次加速, 在落到海床的瞬间 Z 方向的框架速 度变向, 在框架在海床上的翻滚过程中框架在垂直方向 的速度在 Z 轴的正负方向反复变化, 最终为 0. 且流速大 小的变化对框架 Z 方向的运动速度影响不大; 而在 X 方 向, 随着海流流速的增大, 框架的速度在同一时刻逐渐增大; 且对于某一海流流速作用下的框架而言, 在整个 时域上框架在 X 方向的速度呈现出先正向增大然后到达 一定深度后速度开始减速, 在框架在与海床接触瞬间的 X 方向的水平速度值再次正向急剧增大, 随即又由于翻 滚过程中海床的阻碍作用瞬间减小到某一负值, 此后在 翻滚的过程中框架 X 方向的水平速度反复正负变化, 最 后框架 X 方向的速度在框架在海床上的翻滚过程中逐渐 降为 0; 也就是说在框架在海床上翻滚的过程中海床对 框架的 X 方向的水平运动既有阻碍作用又有促进作用, 且两种作用在框架的翻滚过程中是相互交替的 。框架的 平动加速度图像 (图 16) 也说明了这一点。
经仿真发现, 框架在流向为 0 °保持不变, 流速增加 的情况下, 框架的转动主要集中在纵摇方向上, 因此框 架在横摇和艏摇方向的转动图像不再给出。
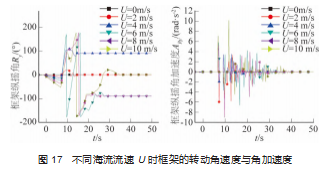
观察框架的纵摇转动图像 (图 17 (a) ) 发现, 在 流向为 0 °时, 在框架与海床发生接触前, 在初步入水后 框架就开始缓慢发生小范围的转动, 且这种转动幅度随 着流速的增加而增加; 框架的剧烈大幅度反复转动主要 发生在框架与海床开始接触到框架停止在海床上滚动这 一过程阶段之间, 且转动主要集中在框架的纵摇方向 (横摇和艏摇几乎为 0), 流速越大, 框架的最大纵摇角 就越大 。且当流速为 0 时, 框架落在海床上以后并没有 发生转动, 这说明在海流流速为 0 时, 虽然有海床与框 架的相互作用, 但这种作用不会使框架发生翻滚 。结合 第 3. 1 节得出的结论可以知道, 当海流流向为 0 °时, 在 海流不随着水深衰减的条件下, 框架发生翻滚需要海流 有着一定的流速且框架与海床有着瞬间的相互接触碰撞,单一的海流作用仅仅会使得框架发生沿 X 方向的平动; 单一的海床作用力仅仅会使框架发生 Z 方向的垂直运动。
框架的转动角加速度 (图 17 (b) ) 显示, 框架的 角加速度变化也是主要集中在框架与海床开始接触到框 架停止在海床上滚动这一过程阶段之间, 且角加速度的 变化也主要集中在框架的纵摇方向, 且流速越大, 最大 转动角加速度越大, 在艏摇和横摇方向框架的角加速度 数量级为 1015 m/s2. 几乎可以忽略。
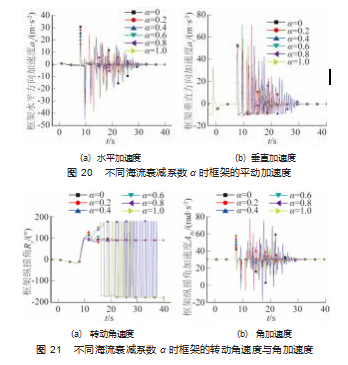
3.3 海流衰减系数对框架的下放入水过程的影响
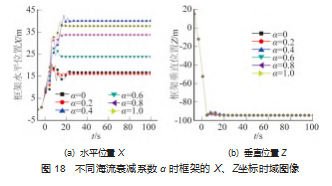
不同海流衰减系数时框架的 X、Z 坐标时域图像如图 18 所示。
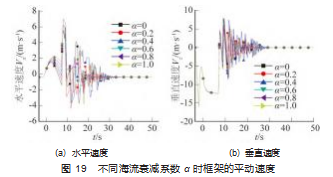
需要指出的是, 衰减系数越大, 海流在海平面与海 底的差值就越小, 如果衰减系数为 1. 则表示海流沿水 深方向没有衰减 。观察图 18 (a) 发现, 落地之前框架 整体沿 X 轴正向外飘, 衰减系数越大, 外飘距离越大 。 且可以看出, 在流向不变时, 流速沿深度的衰减对框架 Z 方向的下落几乎无影响 。经仿真发现, 框架在流向为 0 °保持不变 、流速沿着水深衰减的情况下, 框架的转动 主要集中在纵摇方向上, 框架的平动主要集中在 X 方向 和 Z 方向, 因此框架在横摇和艏摇方向的转动图像以及 在 Y方向的平动图像都不再画出 。 由图 18 框架的平动位 置图像可知, 框架在 35 s 左右的时候就已经停在了海床 上, 为便于数据的采集和观测, 图 19~21 仅给出前 40 s 的静平衡阶段到动态仿真阶段的仿真结果。
流速沿水深的递减使得框架上下部分流体的拖曳冲 击力不同, 因而形成了一个使得框架会有向 X 轴正向翻 滚趋势的力矩, 触地瞬间, 海床与框架发生剧烈碰撞, 此时框架底边框受到海床对其的强力冲击载荷, 这个力矩与海床对框架的冲击载荷会使得框架在此刻发生沿 X 轴正向的剧烈翻滚; 而且随着海流衰减系数的增加, 框 架在触地瞬间的翻滚剧烈程度依次减小, 这是由于随着 海流衰减系数的增加, 框架上下端的流体拖曳冲击力的 差值变小, 从而形成的翻滚力矩越来越小, 翻滚力矩越 小,
在框架与海床接触的瞬间框架发生翻滚的急剧程度 越小 。且此时应该注意框架 4 根水平布置的边框 (与 Y 轴平行的 4 根), 因为在这种情况下这 4 根边框会受到强 烈的扭转载荷, 在实际工程实践中在这种海况下布放框 架时, 要对这 4 根边框做抵抗扭转的预防措施。
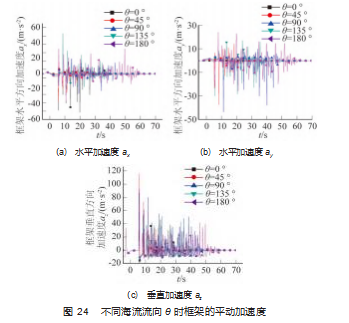
3.4 海流流向随水深变化时海底流向角的变化对框架下 放入水过程的影响
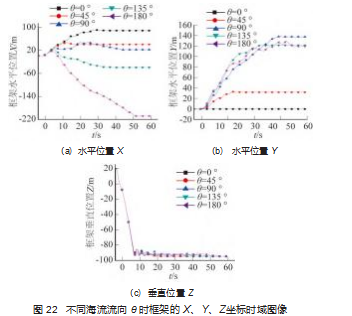
需要指出的是, 当水流在海床的流向仍为 0 °时, 说 明此时海流在整个水深的方向没有发生变化。
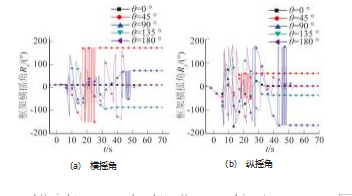
观察不同海床流向时框架在 X、Y、Z 3 个坐标轴的 位置时间图像可知, 海流流向随水深的变化对框架在 XY 平面的运动轨迹有着明显的影响, 而对框架 Z 方向的下 落无明显影响 。当海底海流流向小于 90 °时, 随着海床 流向角度的增加, 框架最终稳定时在 X 轴正方向的位置 时其正向的 X 坐标值越小, 这是由于当海底海流流向小 于 90 °时, 随着海底的流向逼近 90 °, 单位水深引起的 流向变化越来越快, 海流作用力在 Y 轴正向的分量越来 越大, 海流作用力在 X 轴正向的分量越来越小造成的; 且海床与海流的联合作用下, 在海床流向为 90 °时框架 在与海床接触的瞬间会发生沿 X 轴负向的翻滚, 造成最 终稳定后 X 正方向的位移减小 。而在海床流向小于 90 ° 时, 虽然海床与海流的联合作用也会导致框架发生翻滚, 但这种作用并不会造成框架落到海床上以后发生沿 X 轴负方向的运动 。也就是说, 当海床流向小于 90 °时, 框 架沿 X 轴正向移动, 且其在 X 轴位置的正向坐标在时域 上先增大, 后不变; 而当海床流向达到 90 °时, 框架在 X 轴位置的正向坐标在时域上先增大后减小直至其停在海 床上; 且在海床流向在 0 °~90 °变化时, 框架在 X 轴上的 平动运动达到稳定所需的时间先减小后增加 。而在海床 流向超过 90 °以后, 随着海床流向逼近 180 °, 单位水深 引起的流向变化产生的沿 X 轴负方向的分量越来越大, 因此框架在 X 轴负方向的位移越来越大, 且框架在 X 轴 上的平动运动达到稳定所需的时间也越来越长 。当海底 海流流向小于 90 °时, 随着海床流向角度的增加, 框架 最终稳定时其正向的 Y 坐标值越大, 框架在 Y 轴上的平 动运动达到稳定所需的时间也越来越长; 当海床流向超 过 90 °以后, 随着海床流向向 180 °逼近, 由于单位水深 引起的流向变化产生的沿 Y 轴正方向的分量越来越小, 框架稳定停在海床上时在 Y轴正向的位移幅度逐渐减小, 但框架始终还是会向 Y 轴正向运动, 且在 Y 轴正向运动 达到稳定所需的时间先减小后增大。
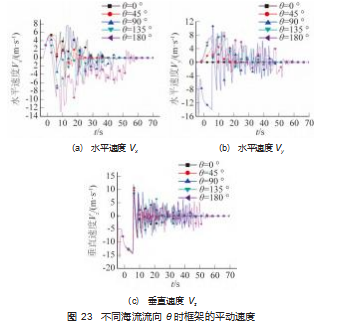
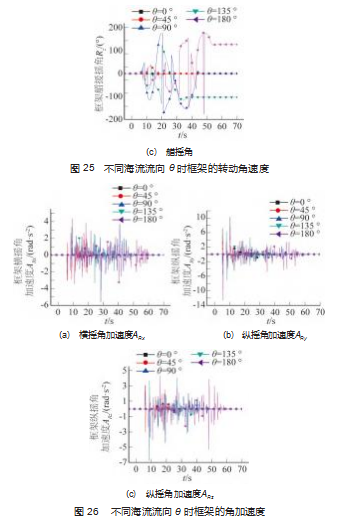
观察图 23~26 框架 3 自由度平动的运动速度 、角速 度 、加速度 、角加速度在时域上的变化情况可知: 当海 流流向随着水深的变化而变化时, 框架在 X 和 Y 轴的运 动速度在海床流向角超过一定角度后会产生沿 X 轴和 Y 负向的速度分量, 且 Y 负向的运动分量在时域上存在的 时长较短; 海流流向随水深的变化除了会影响框架的平 动位移外, 由于不同水深的海流方向的不同会形成一个 转动力矩, 导致框架自身发生复杂的 3 自由度组合转动, 框架在 3 自由度方向的转动角加速度显示, 单位水深流 向变化越快, 3 自由度的组合转动就越复杂 。框架 3 自由 度转动角加速度显示, 这种情况下, 框架艏摇 、横摇和 纵摇方向的变化极其复杂, 工程实践中, 框架的各个杆件边框承受了复杂的弯扭载荷, 尤其是扭转载荷, 其中 纵摇方向的扭转尤其剧烈, 承受这种扭转载荷的主要构 件是框架的 4 根与 Y 轴平行的边框 。在保持流速不变的 情况下, 海面流速的方向与海底流速方向的差距越大, 扭转效应越明显, 框架主体在下落过程中越有可能发生扭转变形, 尤其是在海流流速特别大的海域 。在实际工 程中应注意对海域流向的变化进行合理选取, 对于海流 流向随水深变化特别快的海域, 应采取有效措施以保证 施工作业期间框架不发生大幅度的艏摇转动 、框架边框 不发生大的扭转变形 。也就是说在海流流向随水深变化 的前提下, 框架从入水到开始接触海床这一阶段内会发 生复杂的 3 自由度转动运动, 且流向角随着水深变化得 越快 (单位水深内流向的改变度数越大), 框架的 3 自由 度转动运动越急剧; 且由于在艏摇 、横摇纵摇 3 个方向 都发生了转动, 在实际工程中框架的 12 个边框都会受到 强烈的扭转作用, 其中与 Y 轴平行的 4 个边框受到的扭 转作用最大, 与 X 轴平行的 4 个边框受到的扭转作用和 与 Z 轴平行的 4 个边框受到的扭转作用相差不大 。如在 这种海况下进行施工, 尤其要注意对与 Y 轴平行的 4 个 边框进行抗扭转作用方面的加强。
4 结论
本文针对大型框架的入水过程中的动力学特性问题, 设计了一种大型六面十二边透水刚性框架以研究不同海 洋环境载荷对其入水过程的影响 。研究结论如下。
( 1 ) 入水瞬间会有很大的抨击力使得框架速度和加速度发生较大变化, 可从相关的速度和加速度图像中得 到 。可考虑在框架底部表面添加一层多孔泡沫塑料减小 瞬间入水抨击力 。但会提高框架受到的浮力, 进而增加 框架在水中垂直方向的下落时间 。因此, 需要时可以通 过计算, 改变添加在框架表面的多孔泡沫塑料的层数, 减小波浪抨击力的同时在某种程度上控制框架在水中的 下落时间。
( 2 ) 从入水瞬间框架速度的衰减情况和加速度的变 化情况可以得到, 不同的参数对框架入水瞬间的抨击力 影响不大 。因此, 除去抨击力的因素外, 影响框架在水 中垂直下落时间的主要因素是框架最初的入水速度, 即 框架在起重船上的吊放高度。
参考文献:
[ 1] 蔡怡希, 张晏瑲 . 南海争议区油气资源开发的法律困境和对 策[J]. 南海学刊, 2017. 3(4): 17-26.
[2] 张奇 . 建设粤港澳大湾区水上机场体系的战略思考[J]. 民航 管理, 2019(3): 38-40.
[3] 刘国良, 覃振东, 汤伊琼 . 水上机场平面布置要点探究[J]. 港 工技术, 2018. 55(2): 12- 16.
[4] 王广大, 毛筱菲 . 水上机场助航波能灯浮标的波能俘获优化 [J]. 中国舰船研究, 2017. 12(6): 15-21.
[5] 王庆国, 毛文江 . 海上平台燃气轮机发电机组滑动轴承异常 磨损故障分析[J]. 机电工程技术, 2022. 51(4): 251-254.
[6] 邓海超 . 加拿大水上机场布局建设情况[J]. 空运商务 , 2018 (9): 47-49.
[7] 杨勇, 王加龙, 许伟, 等 . 海上平台换流站温排水数值模拟[J]. 机电工程技术, 2022. 51(3): 307-310.
[8] 潘正华, 刘文杰, 王维国, 等 . 三亚湾水上飞机临时起降场项 目的探索与实践[J]. 中国民用航空, 2014(3): 45-47.
[9] 李煦 . "局座 "张召忠: 建"百年海军 "我们还需努力[N]. 长江日 报, 2019-04-30(25).
[10] 张召忠 . 英国要把女王级航母设计图交给印度?[N]. 科技日 报, 2019-04- 10(05).
[ 11] 蒋桂通, 寇玉全, 路正道,等 . PAUT 技术在海洋石油平台卷管 焊缝检验上的应用[J]. 机电工程技术, 2022. 51(5): 276-278.
[ 12] 李杰, 徐亚玲, 王君如, 等 . 半潜式平台压排载系统设计与调 载应用[J]. 机电工程技术, 2022. 51(1): 205-208.
[13] 张延昌, 刘昆, 王璞, 等 . 大型浮式结构物结构碰撞性能分析 [J]. 船舶, 2015. 26(6): 1-7.
[ 14] 徐磊, 张美丽 . 可移动浮式 LNG 传输平台方案研究[J]. 机电 工程技术, 2021. 50(12): 242-245.
[15] 滕斌, 勾莹 . 大型浮体水弹性作用的频域分析[J]. 工程力学, 2006(S2): 36-48.
[16] 黄挺, 田英辉, 李俊龙, 等 . 马尔代夫海域大型海洋浮体模块 选型及优化[J]. 大连理工大学学报, 2022. 62(1): 85-94.
[ 17] 陈勇, 石锦坤, 王勇, 等 . 基于DNV 规范的结构物吊装入水简化 算法及其适用性分析[J]. 中国海上油气, 2014. 26(S1): 63-65.
关注SCI论文创作发表,寻求SCI论文修改润色、SCI论文代发表等服务支撑,请锁定SCI论文网!
文章出自SCI论文网转载请注明出处:https://www.lunwensci.com/ligonglunwen/60844.html