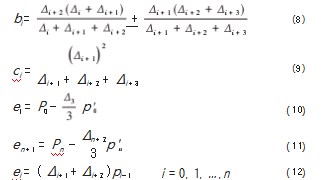SCI论文(www.lunwensci.com)
摘要:对多自由度运动轨迹进行仿真时存在轨迹不平滑,曲面重合度低等问题。因此提出了一种以五维空间样条曲线为理论基础的插补算法。算法以五自由度运动为研究基础,可以将离散的五坐标数据统一到五维空间样条曲线上,建立对应的数学模型,直观地对其进行分析处理,输出平滑的轨迹曲线曲面,最终在计算机上实现运动轨迹仿真。还提出一种基于Hausdorff距离求解法的拟合曲线和原始曲线进行重合度比较的算法,可以直观地输出曲线间距变化折线图并算出两条曲线的重合度,并以这种比较算法对本文插补算法与常用的双样条插补算法进行比较。综合实验得出的重合度比较结果和运动角度变化曲线,结果本文算法输出的运动轨迹更为平滑,与原始设计运动轨迹重合度更高。
关键词:运动轨迹仿真;五维样条;双样条;插补算法
Five Dimensional Spline Interpolation Algorithm and Its Application
Jin Yuequan1,Zhu Kongfeng2,Yan Jihong2,Wang Xingbo1※
(1.Department of Mechatronic Engineering,Foshan University,Foshan,Guangdong 528000,China;
2.GSK CNC Equipment Co.,Ltd.,Guangzhou 510530,China)
Abstract:There are some problems in the simulation of multi-degree-of-freedom(multi-DOF)motion trajectory,such as unsmooth trajectory and low surface coincidence.Therefore,an interpolation algorithm based on five-dimensional spatial spline curve is proposed.The algorithm is based on five-DOF motion,it can unify the discrete five coordinate data onto the five dimensional space spline curve,establish the corresponding mathematical model,intuitively analyze and process it,output the smooth track curve and surface,and finally realize the motion track simulation on the computer.An algorithm based on Hausdorff distance solution method is also proposed to compare the coincidence degree between the fitting curve and the original curve,which can intuitively output the broken line chart of curve spacing change and calculate the coincidence degree of the two curves.This comparison algorithm is used to compare the interpolation algorithm in this paper with the commonly used double spline interpolation algorithm.According to the comparison results of coincidence degree and the curve of motion angle change obtained from the comprehensive experiment,the motion trajectory output by the algorithm in this paper is smoother,and the coincidence degree with the original design motion trajectory is higher.
Key words:motion trajectory simulation;five-dimensional spline;double spline;interpolation algorithm
0引言
三维空间样条被广泛应用在运动轨迹仿真中[1-4],例如运动轨迹的规划,运动物体轨迹的定位等。但随着控制复杂度的增加,运动轨迹自由度也在增加,例如机械臂的旋转角度[5,6],数控系统五坐标加工[7-9],如何建立这些多自由度运动模型[10],实现运动轨迹仿真分析,是众多研究者的关注热点。在一些五坐标运动轨迹,例如五坐标侧铣加工的描述中,双样条插补算法是一种实用直观的插补算法[11-13]。在西门子的数控系统中也有所应用[14],但西门子还有以其他数据形式描述五坐标运动轨迹的方式[15-16]。因为双样条插补算法本身在数学基础上存在问题,其仿真出的运动轨迹上下准线与原始设计轨迹能保持较高重合度,但上下准线相连的导线所成运动轨迹曲面却并不能和原始设计运动轨迹曲面保持一致。故本文提出了一种五维空间样条插补算法,可以对离散的五坐标数据进行处理,最终仿真出与原始设计运动轨迹重合且坐标变换平滑的运动轨迹曲面。在本文中还对双样条插补算法进行了复现与本文提出算法进行了重合度比较实验。
本文按照如下顺序介绍相关内容:首先是所用的空间样条曲线基本知识,Hausdorff距离求解法,五维空间样条插补算法,重合度比较算法,双样条插补算法复现仿真效果和重合度计算结果,五维空间样条插补算法仿真效果和重合度计算结果。最后对两算法重合度结果进行比较。
1曲线定义和Hausdorff距离求解法
1.1 B样条曲线
给定一组控制点Pi(i=0,1,…,n),可定义一条k阶B样条曲线。
式中:ui为节点矢量的第i个元素;参数u从umin到umax;规定:0/0=0;
1.2 Hausdorff距离求解法
Hausdorff距离求解法原理是在给定的欧式空间中,对两个点集A={a 1,a2,a3,…},B={b 1,b2,b3,…}进行近似间距求解,如式(3)所示。
式(3)中H(A,B)为双向Hausdorff距离。式(4)中:ℎ(A,B)为从点集A到点集B的单向Hausdorff距离;ℎ(B,A)为从点集B到点集A的单向Hausdorff距离。
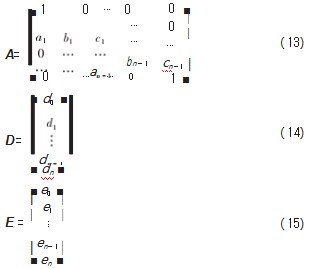
2五维样条曲线插补算法
给定一组五坐标数据点Pi(i=0,1,…,n),形如(X,Y,Z,A,B),使用积累弦长参数化法对Pi进行参数化,具体见式(5)。
根据前述求出的参数代入展开后,使用追赶法进行计算,具体追赶法实现步骤如下:令
原式化为AD=E,首先对A矩阵进行分解:A=LU,其中
di=yi−ui×di+1(20)
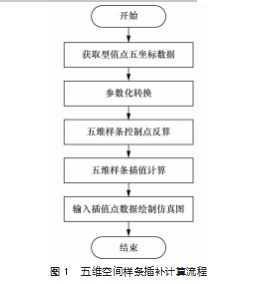
最终求出一系列五维空间控制点坐标di(i=0,…,n+2),再将这些控制点代回式(1),输出插值点数据,并绘制出仿真图。
前述原理归结成流程如图1所示。
3重合度比较算法
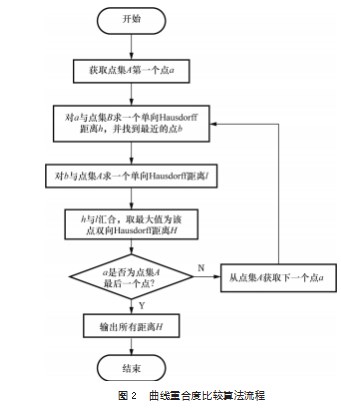
本小节以前述Hausdorff距离求解法为基础,提出一种重合度比较算法,具体步骤如下:
步骤一:给定两条待比较曲线型值点点集A{a0,a 1,…,an}和点集B{b0,b 1,…,bm};
步骤二:获取点集A第一个点a0,将其与点集B按照式(4)求一个单向Hausdorff距离ℎ,并记录最近点ba0;
步骤三:将ba0与点集A按照式(4)求个单向Haus⁃dorff距离l;
步骤四:汇集ℎ和l,取其中的最大值为该点双向Hausdorff距离H0;
步骤五:获取点集A的下一点a,然后重复步骤二至步骤四,直至读取完点集A中所有点;
步骤六:汇集所有双向Hausdorff距离H组成一个集合Hi,i=0,1,…,n;
上述步骤归结成流程如图2所示。
通过本结比较算法算出所有距离集合Hi后,其中距离大于0.05 mm的位置,就认为是不重合的位置,重合度以式(21)进行计算:
f=(p/n)×100%(21)
式中:p为误差超过0.05 mm的位置的点数;n为点集A总点数。
4实验比较
4.1双样条插补算法复现仿真比较
通过整理前述所提文献的算法,以其中所提到常用的插补方法对一个线性插补的5坐标加工数控程序重新建模插补计算,并仿真出其刀轴运动轨迹。这个数控程序原始设计是通过五坐标侧刃加工出S试件,程序中的原始文件为S试件根部轨迹离散点坐标值和刀轴运动到这些离散点位时,刀轴的两个转动角度。插补复现时,首先将角度和下准线坐标值相结合计算出上准线坐标值,再对上下准线进行插补计算,上下准线插补计算过程中独立进行参数化和控制点反算,各自使用自己控制点计算出的节点矢量参数,最后在插值点计算过中保持上下同步。本次仿真复现时取刀轴长度为50 mm,及上下准线初始连接所成导线长度为50 mm。通过插补计算后输出上下准线插值点数据,并通过Arx程序在CAD软件中做出仿真效果如图3所示,仿真图显示出了上下准线的轨迹,并以上下准线同步的插值点连线作为直纹面[17,18]导线,组成完整的运动轨迹仿真图。由图3可以看出,双样条插补算法可以仿真出一个完整的刀轴运动轨迹曲面,但并不能直观看出轨迹变化是否平滑,并评估仿真效果是否达标。故本文选取了上准线和曲面腰线进行了具体分析。图4为重新插补计算出的上准线与原始设计上准线重合整体比较图。
由图4可以看出双样条插补算法做出的上准线与原始设计上准线高度重合。选取上下准线插值点连线所成刀轴轨迹仿真直纹面的腰线作为仿真出的曲面重合效果评估参考线,将其与原始设计运动轨迹曲面腰线重合进行比较,结果如图5所示。
对圆圈位置放大5倍,结果如图6所示。图中三角形标记的曲线为双样条插补算法做出的运动轨迹曲面腰线,正方形标记的曲线为原始设计运动轨迹曲面的腰线。从图6可以看出,两者大相径庭。
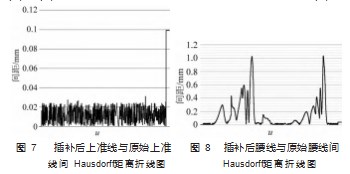
对上述两组轨迹使用前述重合度比较算法进行比较,输出两组轨迹曲线间距并绘制距离折线图,结果如图7~8所示,图7为插补后上准线与原始上准线间Hausdorff距离折线图,图8为插补后腰线与原始腰线间Hausdorff距离折线图。
从图7可以看出,插补后上准线与原始上准线大部分位置的间距都在0.2 mm左右,使用重合度比较算法可以算出其仅有2.12%的位置误差超过了0.05 mm,重合度为97.88%。可见双样条插补算法仿真的上准线与原始设计运动轨迹上准线高度重合。由图8可得,双样条插补算法仿真出的曲面腰线与原始设计运动轨迹曲面腰线的间距最大的甚至超过了1 mm,其中超过了0.05 mm的位置占整条轨迹的61.52%,重合度仅有38.48%。
综合上述实验数据,可见双样条插补算法可以仿真出完整的运动轨迹,但除了上下准线外,其他导线位置重合度不高。为进一步探讨其问题出现原因,下面将把双样条插补算法插补计算出的角度变化与本文算法插补计算出的角度变化一起进行比较分析。
4.2五维样条曲线插补算法比较
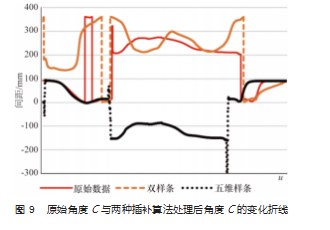
以4.1节中用到的数控程序作为测试样本,以本文提出的五维空间样条曲线插补算法对其进行插补处理。其角度变化经过平滑处理后,原本存在的大幅度角度变化被处理掉,上准线在CAD中显示出的形状会与双样条插补算法中显示出的略微不同。以运动轨迹导线角度C的变化为例,将原始运动轨迹导线角度C的变化与两种算法插补处理后的角度C变化绘制到同一张折线图中进行比较,结果如图9所示。图中实线为原始运动轨迹角度C的变化折线图,短划线为双样条插补算法处理后角度C的变化折线图,点线为五维样条插补算法处理后角度C的变化折线图。由图9可以看到,双样条插补算法处理后角度C与原始有明显不同,同时还存在3处断崖式大幅度变化。而五维样条插补算法,前后两段都与原始的几乎重合,且更为平滑,为减少中间段出现的大幅度变化带来的不平滑性,本算法对其进行了360°旋转,消除了大幅度的角度变化,同时还能保持导线矢量方向不变,然后按照其整体变化,对其实现了平滑处理。最后处理后的角度变化大部分变化趋势都能保持和原始的相似,但是在数值上确实存在了一些变化,但本文算法是统一对五坐标进行的处理,关键是最后综合仿真出的运动轨迹是否重合,因此,还需要对其仿真出的轨迹进行具体比较分析。
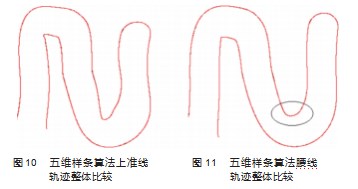
同样选取仿真出的运动轨迹上准线与原始设计运动轨迹上准线进行重合比较,如图10所示。由图可以看到仿真出的运动轨迹曲面上准线和原始设计运动轨迹上准线,两者几乎完全重合。为检测其是否能仿真出原始设计运动轨迹曲面,取仿真出的运动轨迹曲面腰线与原始设计运动轨迹腰线重合比较,结果如图11所示,重合度仍然极高,几乎分辨不出误差。
取与双样条插补算法重合比较时相近标记位置放大5倍得到图12。图中,三角形标记的曲线是仿真出的运动轨迹曲面腰线,正方形标记的曲线是原始设计运动轨迹曲面腰线,两者几乎完全重合。
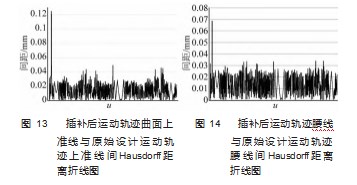
用重合度比较算法对这两组轨迹进行分析,输出两组轨迹曲线间距,并绘制距离折线图,结果如图13~14所示。
其中图13为插补后运动轨迹曲面上准线与原始设计运动轨迹上准线间Hausdorff距离折线图;图14为插补后运动轨迹腰线与原始设计运动轨迹腰线间Hausdorff距离折线图。由图13可以看出,两上准线间距少有超过0.04 mm的,几乎都在0.02 mm附近波动,重合度比较算法可以算出其仅有0.28%的位置误差超过了0.05 mm,重合度为99.78%。由图14可以看到,两腰线间距折线图波动变化虽然与上准线的折线图波动变化略有不同,但是也在相近位置出现误差超过0.05 mm,其他位置都在0.03 mm以下,在0.01 mm附近波动,同样用重合度比较算法可以算出其重合度也有99.78%。
5结束语
本文以五坐标加工为研究基础,仿真其刀轴的运动轨迹。复现了双样条插补算法对五坐标运动轨迹的插补仿真,通过分析仿真出的直纹面腰线重合度,可以看到双样条插补算法仿真出的运动轨迹只能保证上下准线与原始设计轨迹重合。通过进一步分析导向矢量变化发现,出现大角度突变的原因是其直纹面导线由上下准线插值点连接而成,易形成拼接绞点,在这些位置的导线矢量方向与原始设计运动轨迹矢量方向不同,使得最终仿真出运动轨迹不平滑。本文算法对五坐标数据建立了统一的五维空间样条曲线模型,减少了大角度突变,使最终仿真出的运动轨迹更为平滑。
进一步综合比较两种算法仿真出的运动轨迹腰线与原始设计轨迹腰线的重合度,可以看出,本文算法最终仿真出的运动轨迹曲面的仿真效果要优于双样条插补算法的仿真效果。
后续本算法还将扩展应用到其他五自由度运动轨迹仿真测试中,例如机械臂旋转摆动的运动轨迹,导弹等飞行物空中姿态模拟等。且这种多维空间曲线的算法应用也可以给更高自由度运动轨迹仿真作为参考。
参考文献:
[1]聂宸,袁楚明,张代林,等.随机型值点间的插值轨迹规划研究[J].机械与电子,2014(3):3-5.
[2]徐雅南.基于B样条曲线拟合非平稳目标运动轨迹的水声数据仿真方法[J].声学与电子工程,2016(2):10-13.
[3]常真瑜,郑海鸥,韩振,等.防空兵虚拟战场中目标运动轨迹拟合算法研究[J].舰船电子工程,2011,31(5):79-82.
[4]刘钊鹏,苏啸,李滨城.基于MATLAB/ADAMS的平面三自由度并联机构的运动学和动力学分析及控制的初步设计[J].机电工程技术,2012,41(6):54-59.
[5]余乐,李庆,郑力新,等.六自由度机械臂运动轨迹自动生成方法仿真与实现[J].华侨大学学报:自然科学版,2018,39(3):355-359.
[6]丁子涵,徐顾自,张虎.四自由度机械臂的轨迹仿真研究[J].内燃机与配件,2022(10):10-12.
[7]李晓磊,吴勇中,桂贵生.双刀车削数控加工仿真技术研究[J].制造技术与机床,2009(6):74-78.
[8]张霞,杨岳.基于AutoCAD的数控加工可视化仿真系统研究[J].计算机技术与发展,2011,21(6):169-172.
[9]任强,罗泽林.基于插补算法与最优前瞻的数控运动轨迹控制研究[J].机械设计与制造工程,2016,45(4):63-66.
[10]韩庆珏,刘少军,金燕.海底采矿移动机器人的避障研究[J].机电工程技术,2006,35(1):45-46.
[11]陈良骥,王永章,富宏亚.五轴联动双NURBS曲线的生成与插补方法研究[J].机械制造,2006,44(1):67-70.
[12]张立强,张守军,王宇晗.基于对偶四元数的五轴等距双NURBS刀具路径规划[J].计算机集成制造系统,2014,20(1):128-133.
[13]黎红石,樊留群,赵建华,等.基于双样条拟合的五轴插补算法[J].制造技术与机床,2021(2):147-156.
[14]邵毅.基于西门子828D双通道功能的五轴协同加工的应用[J].金属加工(冷加工),2022(8):71-74.
[15]王高红,席勇.西门子运动转换功能在BF120-5五坐标加工中心改造中的技术应用[C]//2019航空装备服务保障与维修技术论坛暨中国航空工业技术装备工程协会年会,2019:578-580.
[16]李栋,邓永红.基于VERICUT的五轴卧式机床建模与加工仿真[J].组合机床与自动化加工技术,2018(5):135-138.
[17]张子杰,高淑荣.直纹面的应用与教学[J].河北煤炭建筑工程学院学报,1995,12(4):66-69.
[18]曾君莲.直纹面及其应用[J].中国大学教学,1990(1):32-34.
关注SCI论文创作发表,寻求SCI论文修改润色、SCI论文代发表等服务支撑,请锁定SCI论文网! 文章出自SCI论文网转载请注明出处:https://www.lunwensci.com/ligonglunwen/59938.html