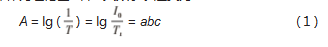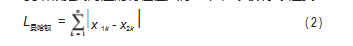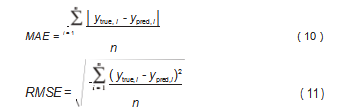SCI论文(www.lunwensci.com)
摘要 :肥胖人群是特殊人群, 通过实时检测血压, 可以预防高血压, 大大降低由高血压引起的各种并发症 。为了解决现有算法对 肥胖人群血压测量准确度不高的问题, 提出一种基于 Stacking 集成机器学习的血压计算模型, 该模型将 K 近邻 、极端随机树 、 lightGBM 回归模型作为初级学习器, 线性回归模型作为次级学习器 。通过使用长桑技术设备提取并建立 PPG 特征值数据集, 将数 据集分成非肥胖人群 ( BMI<25) 和肥胖人群 ( BMI>25), 并把身体质量指数 ( BMI ) 作为新的特征参数加入到模型进行训练和测 试 。实验结果: 在非肥胖人群中, Stacking 模型测量收缩压和舒张压的评价指标 RMSE/MAE 分别为 6.611/5.410 和 4.368/3.242; 在肥 胖人群中, Stacking 模型测量收缩压 (SBP) 和舒张压 ( DBP ) 的评价指标 RMSE/MAE 分别为 6.394/4.979 和 4.350/3.233 。 实验结 果表明, 该 Stacking 模型对肥胖人群的血压计算精度明显高于非肥胖人群, 且测量结果符合 AAMI 国际电子血压计标准 (RMSE< 8 mmHg, MAE<5 mmHg), 提高了肥胖人群血压测量的准确度, 可以应用到生物医学领域。
关键词 :肥胖人群,PPG 信号,Stacking集成模型,血压测量
A Method on Cuffree Blood Pressure Measurement for Obese Population Li Qingfu1. 2. Zhao Yubo2 ※, Zhao Jingbo1. Jiang Zeyu1. 2
( 1. School of Information and Control Engineering, Qingdao University of Technology, Qingdao, Shandong 266520. China;
2. Shandong Institutes of Industrial Technology(Qingdao), Qingdao, Shandong 266101. China)
Abstract: Obese population are special people. Through real-time detection of blood pressure, hypertension can be prevented and various complications caused by hypertension can be greatly reduced. In order to solve the problem of low accuracy of existing algorithms for blood pressure measurement of obese population, a blood pressure calculation model was proposed based on stacking ensemble machine learning .The K-nearest neighbor, extreme random tree and light GBM regression model were taken as primary learners and linear regression model was taken as secondary learners. The PPG eigenvalue data set was extracted and established by using changsang technology and equipment and the data set was divided into non-obese population (BMI < 25) and obese population (BMI > 25) and the body mass index (BMI) was added to the model as a new characteristic parameter for training and testing . The results are as follows: in the non-obese population, the RMSE/MAE of systolic and diastolic blood pressure measured by stacking model is 6.611/5.410 and 4.368/3.242 respectively. In obese population, the RMSE/MAE of systolic blood pressure (SBP) and diastolic blood pressure (DBP) measured by stacking model is 6.394/4.979 and 4.350/3.233 respectively. The experimental results show that the accuracy of the stacking model used is significantly higher than that of the non-obese people, and the measurement results meet the AAMI international electronic sphygmomanometer standard (RMSE < 8 mmHg, MAE < 5 mmHg), which improves the accuracy of blood pressure measurement in the obese population and can be applied to the biomedical field .
Key words: obese population; PPG signal; Stacking ensemblemodel; blood pressure measurement
引言
研究显示, 肥胖是引起高血压的主要因素, 且在肥 胖人群中, 高血压发病率高于同年龄的正常群体的一倍, 年龄越大比例越高[1] 。因此, 准确测量肥胖人群的血压, 对及时发现和治疗高血压非常必要 。 目前有 3 种比较主 流的无创血压测量方法: 台式水银血压计测量法, 示波 器电子血压计测量法[2], 基于光电容积脉搏波 ( PPG ) 测 量血压法 。前两个方法都是通过对袖带气囊的充放气实 现对血压的测量, 目前市面上使用的袖带过短, 找到适合肥胖人群的袖带成为一种问题[3] 。 因肥胖人群胳臂粗 大, 有可能得到不正确的血压值 。因此为了摆脱袖带的 束缚, 基于光电容积脉搏波 ( PPG ) 技术测量血压的方 法应运而生, 其具有成本低廉 、容易采集等优点, 成为 最近几年研究的重点[4]。
2017 年, Miao 等[5]利用线性回归模型结合 PPG 信号 中的 14 个特征参数进行血压测量, 虽然降低了舒张压的 平均误差, 但该方法舍弃了对血压非线性影响的特征参 数, 导致总体上对收缩压测量精度不高 。2018 年, Syed等[6]使用昆山兰大学采集的包含年龄 、性别 、身高等生 命体征数据集, 提取原始 PPG 信号及其相应的收缩压和 舒张压, 分别建立回归树 、多元线性回归 、支持向量机 ( SVM ) 模型, 发现加入生命体征信息之后, 回归树模型 可以使血压测量结果达到 AAMI 标准 。 同年, Wang 等[7] 建立多参数的人工神经网络模型 ( ANN ), 将 PPG 特征 反馈给多层感知器结构, 该结构有 22 个输入神经元和 2 个输出神经元, 以同时估计 SBP 和 DBP, 虽然获得了更 好的精度, 却耗费了时间成本和内存成本 。2019 年, 吴 绍武等[8]通过提取 PPG 信号中 (如波谷与波峰的水平距 离 、纵向距离 、斜率等) 15 个特征参数, 建立 lightBGM 模型, 且在原有特征参数的基础上加入历史血压, 提高 了舒张压测量精度, 但因测试数据不一致, 使得收缩压 测量精度比线性回归模型差 。2020 年, 贺楚芳[9]基于 PPG 信号的形态学特征并结合生命体征信息, 建立极端 随机树和随机森林血压测量算法, 发现与线性模型的拟 合程度相比, 非线性模型的性能更好。
近几年针对 PPG 信号进行血压测量的研究存在两 个缺陷: ( 1 ) 很多研究基本上都是用单一机器学习算法 模型进行训练, 而将集成机器学习方法应用于血压测量 的相关研究非常少, 导致血压测量效果不好; ( 2 ) 很 多算法都是对全部人群的血压测量数据进行模型训练, 没有把肥胖人群分开 。有研究表明, 用此算法测量肥 胖人群的收缩压时, 其结果普遍偏低[10] 。这就造成一 个问题, 由于肥胖人群特殊的情况, 血压测量不准确 可能会错过高血压的最佳治疗时间, 造成不可忽视的 后 果 。 因 此, 本 文 在 前 人 研 究 的 基 础 上, 构 建 基 于 Stacking 集成机器学习模型, 在提取的 43 个特征参数 的基础上, 把 BMI 的数值作为新的特征参数加入到模 型 中, 分 别 对 非 肥 胖 人 群 ( BMI<25) 和 肥 胖 人 群 ( BMI>25) 数据集进行模型训练, 并与文献[5] 、文献[8]、 文献[9]用到的机器学习方法进行结果对比, 构建对肥 胖人群血压测量有着更高精度的算法模型 。本文的主 要的创新点如下 。
( 1 ) 选用多功能参数仪, 设计采集实验, 采集志愿 者的 PPG 信号和真实血压值, 然后依次进行降噪处理、 特征参数提取, 建立了区别于目前大多数研究使用的 MIMIC 血压数据集的新数据集。
( 2 ) 整合 K 近邻 、极端随机树 、lightGBM 、线性回 归单一机器学习模型, 提出基于 Stacking 集成机器学习 血压测量模型, 弥补了单一模型的不足。
( 3 ) 将人群分类研究, 把训练数据分成非肥胖人群 ( BMI<25) 和肥胖人群 ( BMI>25), 并把 BMI 数值作为 特征输入, 提高了肥胖人群的血压测量精度。
1 实验数据集建立
目前很多研究使用的 MIMIC-II 数据集虽然包含心血 管患者的 PPG 信号波形以及血压值[11], 但是因其信号失 真严重, 处理起来难度大, 且缺乏患者的身高 、体重、 年龄等生理信息, 故需建立一个更适合本算法的数据库。 1.1 PPG 原理光电容积脉搏波描记法 ( PPG ) 以 Lambert-Beer 定 律作为理论基础, 其数学表达式为:
式中: A 为吸光度; T 为透过血液容积的强度 It 与入射光 强度 I0 的比值; a 为吸收系数; b 为吸收层厚度; c 为血 液的浓度[12]。
基本原理: 当红蓝光照射到如手指等皮肤时, 骨骼、 肌肉等组织对光的吸收基本不发生改变, 而心脏的搏动 是有节奏的, 血液随着心脏搏动运输各种人体所需的营 养物质的过程中, 动脉血管的血液容积不断发生改变 。 利用光电传感器测量到此种变化, 然后经信号转换形成 光电容积脉搏波信号 ( PPG 信号)。 通过相关算法提取 PPG 信号中的特征参数并与真实血压值进行回归分析, 就可以得到血压值与特征参数之间的算法模型[13]。
1.2 PPG 信号采集
本研究使用某公司研发的多功能参数仪采集了某小 区 540 位年龄在 25 ~ 80 岁的健康志愿者的 PPG 信号以及 使用鱼跃水银血压计采集了真实血压 。告知每位志愿者 在参加测试之前不做剧烈运动, 不饮用可乐 、咖啡 、酒 水等影响心血管系统的饮品 。志愿者将个人体征信息填 写完毕之后, 处于静坐姿势, 然后佩戴仪器开始采集 PPG 信号和真实血压值 。 以每天 11:00- 12:00 、 14:00- 15:00 、17:00- 18:00 为固定的采集时间, 每次测量时长 为 3 min, 连续测量半个月并做好记录 。然后整理所有实 验数据以矩阵的形式存放在 Matlab 的 mat 文件中, 该数 据集由矩阵的单元格 cell 阵列组成, 每个单元格 cell 都是 一个矩阵形式, 将其命名为 RAWDATA。
1.3 信号预处理
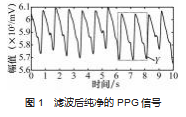
在采集过程中, 因测试者操作不当或身体的抖动, 导致早期 PPG 信号含有毛刺 、高频噪声和基线漂移等噪 声干扰[14] 。为了得到纯净的 PPG 信号, 需要对 RAWDA‐ TA 数据进行预处理 。因 II 型切比雪夫滤波器的幅频特性 具有等波纹特性, 且冲激响应不变[15], 因此为了保证 PPG 信号的完整性, 使波形形状不发生任何变化, 选用 II 型切比雪夫滤波器, 滤波器参数截止频率 FC 、高通频 率 FH 、低 通 频 率 FL 、频 率 响 应 的 纹 波 PR 依 次 设 置 为 FC = 0.4 Hz 、FH = 50 Hz 、FL = 0.2 Hz 、PR = 5. 然后Matlab 软件进行验证和仿真, 选取 10 s 采样样本, 滤波 后纯净的 PPG 信号如图 1 所示。
1.4 特征参数提取
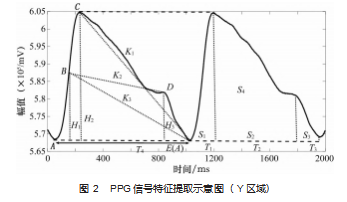
PPG 信号反映了人体心血管健康状况, 其中含有的 生理信息与血压有很大关联[16], 因此在建立血压测量算 法模型之前, 需要对滤波后的 PPG 信号进行特征参数提 取 。具体做法参考文献[17]使用五点平滑 、二阶导数最 大值以及数值微分法, 对 Y 区域进行特征参数提取, 如 图 2 所示。
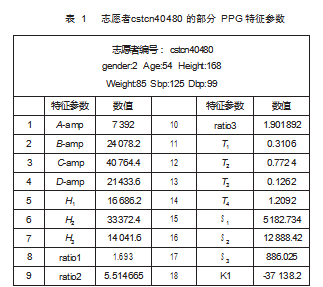
特征参数主要包括: PPG 信号的谷值点 (A 点)、 上 升沿中心点 ( B 点)、 峰值点 ( C 点)、 重搏波节点 ( D 点) 的幅度A-amp 、B-amp 、C-amp 、D-amp, 收缩时间 T1 、峰值点 ( C 点) 和重搏波节点 ( D 点) 的时间间隔 T2. 舒张时间 T2 + T3 、重搏波节点 ( D 点) 和 PPG 信号 结束点 ( E 点) 的时间间隔 T3. 整个心动周期 T4. A 点与 C 点之间的面积 S 1 等。
除了以上提到的时域特征外, 还有一阶导数极值参 数 、二阶导数极值参数等一共 43 个特征参数 。去掉其中 的异常数据和空白信息之后, 最终保留 5 238 条包含年 龄 、性别 、身高 、体重 、特征参数 、真实血压的数据, 保存为 CSV 格式, 以此作为算法模型的数据集 。编号为 cstcn40480 志愿者的部分特征参数如表 1 所示 。模型搭 建 、数据集人群分类以及实验结果将在接下来的章节中 介绍。
2 基于Stacking 血压测量模型
Stacking 集成学习利用了组合策略的思想, 将多个 算法模型组合到一起形成一个更强的模型 。在回归问题 中, 第一层个体学习器 (初级学习器) 先在训练集中单 独训练, 再在测试集中分别输出各自的训练结果, 然后将输出结果作为第二层个体学习器 (次级学习器) 的输 入进行模型训练, 这样做可以使不同个体学习器的能力 得到叠加, 输出一个测量精度更高的结果[18]。
2.1 初级学习器选择
文献[8]将历史血压加入到 lightGBM 算法模型中, 文 献[9]构建极端随机数模型并结合生命体征信息均得到不 错的实验结果 。一致说明某些生命体征信息在传统机器 学习算法测量血压的过程中可以发挥很大作用 。故本研 究采用极端随机树 、lightGBM 、KNN 算法模型作为初级 学习器, 同时加入身体质量指数 ( BMI ) 来训练和测试 数据集。
K 近邻回归 ( KNR ): 是比较经典的机器学习算法, 由于其训练时间少, 又被称作懒惰学习算法[19] 。 由于一 个人的正常血压值随着时间不断发生变化, 故利用 K 近 邻进行血压测量属于回归任务 。KNN 通过相关距离计 算, 选择最近的 K 个邻居的平均值, 进而决策出血压数 据的测量值 。通常选取曼哈顿距离和欧几里得距离。
曼哈顿距离对应的特征值只有一个, 其数学表达式:
欧几里得距离对应的特征值有多个, 其数学表达式:
K 值的选择对算法的最终决策值影响极大, 这直接 影响回归器的性能, 因此合理的选择 K 值, 可以提高训 练结果的精度, 降低估计误差。
极端随机树 ( ETR ): 由随机森林模型变化而来, 和 随机森林一样都以决策树作为基学习器, 但又不同于随 机森林模型[20] 。该模型使用全部的血压数据进行训练, 并且在构建每棵决策树的时候, 随机选择 PPG 信号的 k 个特征参数进行分裂, 在这个过程中, 不修剪树枝 。
端随机树的拟合能力和测量能力都强于随机森林 。极端 随机树对血压测量的步骤为: 第一步选择血压数据集的 全部数据进行训练; 第二步根据 CART 算法, 从 n 个特征 参数中随机选择 k 个生成决策树; 第三步对上面两个步 骤多次迭代, 直至生成所有的决策树, 记为 m; 第四步 重复步骤一至步骤三, 构成随机森林, 通过求森林中多 个决策树对血压的测量值的平均而得到 D 数据集最后的 血压测量值。
LightGBM 回归: 基于树学习的梯度提升框架, 提出 的动机是为了弥补 Xgboot 空间消耗大 、运行时间长 、不 友好的 chche 优化等缺点 。其在运算速度上较 Xgboot 模 型快了好几倍, 占用内存少, 并且处理具有超多数据的 数据集时准确度明显高于其他的算法模型[21] 。其对血压 测量的原理为: 第一是直方图算法, 首先将和血压有关 的特征参数进行离散化, 形成一个宽度为 k 的直方图, 然后依次遍历数据, 寻找直方图上最优的数值; 第二是 带深度限制的 Leaf-wise 算法, 该算法实现每次从当前所 有叶子中, 找到分裂增益最大的一个叶子, 接着进行下 一步的分裂, 依次循环; 第三是 GOSS 技术, 即梯度单 边采样技术, 该技术舍弃那些对于血压测量值没有帮助 的特征参数保留帮助性大的特征参数; 第四为了减少特 征参数过多, 导致测量结果不准确的问题, 互斥特征捆 绑技术可以将相互独立的特征进行捆绑。
2.2 次级学习器选择
为了防止第一层模型在用非线性变化寻求最优空间 假设而产生的过拟合现象, 一般选择比较简单的机器学 习模型作为次级学习器[22], 本研究考虑使用文献[5]中的 线性回归模型。
线性回归算法 (Linear Regression) 表征的是因变量 (目标值) 和自变量 (特征输入) 之间的线性关系, 假设 有 k 个样本数据, 每个样本数据仅有 1 个特征参数, 则线 性回归模型的损失函数为:
y = β0 + β1 x 1 + ... + βk xk ( 4 )
式中: x 1 , x2 , … , xk 为特征输入; y 为目标值; β0 , β 1 , …,βk 为回归系数, 回归系数可通过最小二乘法集中拟合求得, 最小二乘法就是要找到一组 β0 , β 1 , …,βk, 使线性回归模 型的残差平方和方 ( SSE ) 达到最小[23], 从而得到使得 损失函数最小化的拟合函数的模型。
SSE 可表示为:
式中: yβ ( xi )为线性回归模型的测量值; yi 为真实值。
因人体血压值是受多个特征值共同影响的, 则线性 回归模型特征输入 X 是一个 k 维矢量, 此时的线性回归 模型为 y = Xβ, 化成矩阵形式为:
2.3 Stacking 血压测量模型搭建
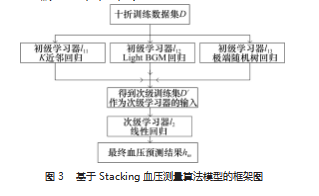
本研究构建基于 Stacking 血压测量算法模型的框架
如图 3 所示 。首先按 8 ∶2 的比例划分数据集, 记训练集为 D = {(x 1 , y 1 ), (x2 , y2 ), … , (xn , yn )}, 其中 x 1 , x2 , … , xn 是与
真实血压值有关的特征参数, y 1 , y2 , … , yn 是对应的每个 志愿者的真实血压值 。为了防止数据量不够而导致训练 结果产生过拟合现象, 将训练集作十折交叉验证处理, 即每次拿 9 份血压数据作为初级学习器 l1i (i = 1. 2. 3) 的训 练集分别进行训练, 剩下的一份血压数据作为测试集, 交叉验证 10 次后加权平均得到 k (k=1. 2. 3 ) 个回归模 型, 此为第一层机器学习模型 。然后以 l1i 个模型输出的 血压测量结果 φl(j)1i [ i = 1. 2. 3. j = size (10 - fold) ] 作为特征 输入, 真实血压值 ym ( m = 1. 2. … , n ) 作为训练标签组成 次级训练集 D´, 最后把 D´放到次级学习器 l2 中进行模型 训练, 此为第二层机器学习模型, 从而得到最终血压测 量结果 hm ( m = 1. 2. … , n )。
3 实验过程与结果分析
3.1 拆分数据集
每个志愿者测得脉搏波参数的量纲不同, 故在训练数据之前首先根据式 ( 7 ) 将脉搏波原始数据标准化为均 值为 0. 方差为 1 的分布, 再根据式 ( 8 ) 将原始数据归 一化至 [ 0. 1 ]区间内, 目的是降低训练权重, 使模型获得更好的训练效果。
式中: Xi 为未处理的数据; Xmax 和 Xmin分别为原始数据的 最大值和最小值。
式中: μ 为未处理数据的均值 (mean); σ 为未处理数据 的标准差 (std)。
本研究将处理过的 5 238 条数据进行数据拆分, 通过 式 ( 9 ) 计算每一条志愿者数据的身体质量指数 ( BMI ) 数值, 然后根据计算结果, 将数据集分成 BMI>25 和 BMI< 25 的子数据集, 并将 BMI 的数值作为新的特征参数输入。
BMI = 志愿者的身高的平方/(志愿者的体重) ( 9 )
式中: 志愿者的体重单位为 kg; 志愿者的身高单位为 m 。 最终得到 3 293 条非肥胖人群的子数据集, 1 945 条肥胖人群子数据集, 分别随机选择每个子数据集的 80% 作为算法模型的训练集, 20% 作为测试集。
3.2 实验过程
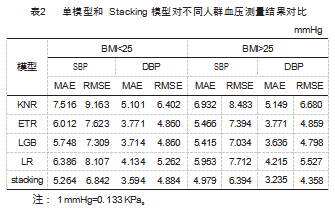
本研究第一个实验是利用单层机器学习模型对 BMI> 25 和 BMI<25 的数据集分别进行训练, 以提取的 43 个特 征参数和 BMI 数值作为模型的输入, 真实收缩压和舒张 压 值 作 为 训 练 标 签 。K 近 邻 回 归 模 型 使 用 枚 举 方 法 、 lightGBM 回归模型和极端随机树使用网格搜索方法进行 超参数优化 、线性回归使用最小二乘法进行调参优化 。 十折交叉验证测试结果显示, K 近邻回归模型最优参数: 距离的权重 weight=distance 、闵可斯基距离为曼哈顿距离 即 P=2 、邻居个数 k= 13 。lightBGM 回归模型最优参数: 每个基学习器的最大叶子节点 、学习率 、基学习器的数 量分别为 num_leaves=31 、learning_rate=0. 1 、n_estimators =40 。极端随机树回归模型最优参数: 基学习器的数量、 决策树最大深度 、最大特征数分别为 n_estimators=50、 max_depth=60 、max_features=11 。第二个实验是利用搭 建好的 Stacking 集成模型, 融合 K 近邻、lightGBM 、极端 随机森林 、线性回归的最优模型对血压数据集进行训练 和测量 。实验一和实验二的结果如表 2 所示。
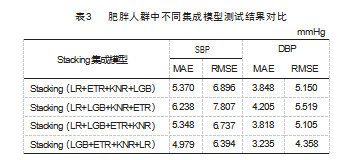
为了与本研究搭建的 stacking 集成模型的性能作对比, 接下来做了第三个实验: 将任意 3 个单模型作为初 级学习器, 另外一个单模型作为次级学习器, 通过不同 的 Stacking 集成模型分别在肥胖人群数据集中进行训练 和测试, 实验结果如表 3 所示。
3.3 实验结果分析
血压算法的准确与否可用平均绝对误差 ( MAE ) 和均方根误差 ( RMSE) 进行评估, AAMI 国际电子血压计标 准为模型的评价指标 MAE<5 mmHg, RMSE<8 mmHg[24]。 其 计 算 公 式 分 别 如 式 ( 10 ) 和 式 ( 11 ) 所 示 。其 中, ytrue, i 为水银血压计测得的真实血压值, ypred, i 为算法模型 的血压测量值, n 为数据总数。
根据表2 和表3 的实验结果, 可以分析得出如下结果。
( 1 ) 对于收缩压 SBP 的测量, 在肥胖人群 ( BMI>25 ) 中 4 个单模型估计的误差 MAE/RMSE 较非肥胖人群 ( BMI<25) 都有所降低; 对于舒张压 DBP 的测量, 在肥 胖人群中 LGB 模型估计的误差 MAE 低于非肥胖人群, ETR 模型估计的误差 RMSE 低于非肥胖人群 。以上结果 显示, 将人群分开且加入 BMI 之后, 虽然单个模型某些 测量结果没有达到 AAMI 标准, 但整体上来说对于肥胖 人群的血压测量精度更高, 符合本研究预期结果。
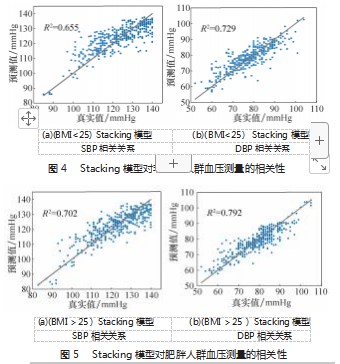
( 2 ) 在非肥胖人群中, 对比最好单模型 ligthGBM 模型, 本研究搭建的 Stacking 集成模型对 SBP 估计的 MAE/ RMSE 从 5.748/7.309 mmHg 下 降 至 5.624/6.842 mmHg, DBP 则 从 3.714/4.750 mmHg 下 降 至 3.594/6.684 mmHg; 在肥胖人群中, 对 SBP 估计的 MAE/RMSE 较 ligthGBM 模 型 从 5.415/7.034 mmHg 下 降 至 4.979/6.394 mmHg, DBP 则从 3.636/4.798 mmHg 下降至 3.235/4.358 mmHg 。此结 果说明 Stacking 集成模型对肥胖人群血压测量精度高于 非肥胖人群, 且满足 AAMI 国际电子血压计标准 。图 4 和 图 5 显示了 Stacking 集成模型对不同人群的收缩压和舒张 压的测量值与真实值之间的相关性 。肥胖人群的 SBP 和 DBP 测量血压与真实血压之间的相关系数 R2 分别为 0.702 和 0.791. 两值之间具有高度相关性, 高于非肥胖人群的 0.655 和 0.729. 进一步说明 Stacking 集成模型对肥胖人群 血压测量精度更高。
( 3 ) 当 LGB 、ETR 、KNR 、LR 中的任意一个作为次 级学习器时, 对肥胖人群血压的测量精度各不相同 。对 于收缩压的测量, Stacking ( LR+LGB+KNR+ETR ) 模型性能最差, 甚至不如 ETR 、LGB 、LR 单模型, 对于舒张 压 的 测 量, Stacking ( LR+ETR+KNR+LGB ) 模 型 和 Stacking ( LR+LGB+KNR+ETR ) 模 型 精 度 不 如 ETR、 LGB 单模型 。无论收缩压还是舒张压, Stacking ( LGB+ ETR+KNR+LR ) 集成模型测量精度最高, 性能最佳。
综合以上所有实验, Stacking ( LGB+ETR+KNR+LR ) 集成模型性能优于 4 个单模型和另外 3 个 Stacking 集成模 型, 且对肥胖人群更有效, 收缩压和舒张压的测量结果 均符合 AAMI 国际电子血压计标准 ( RMSE <8 mmHg, MAE <5 mmHg)。
3.4 Bland-Altman 图分析
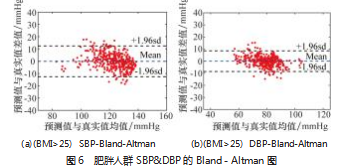
为了进一步评价 Stacking ( LGB+ETR+KNR+LR ) 集 成模型对肥胖人群血压测量的可行性, 对收缩压和舒张压 的测量值与真实值进行 Bland-Altman 分析, 如图 6 所示。
4 结束语
本文建立的 Stacking 集成机器学习模型, 在提取的 PPG 信号特征值的基础上, 把身体质量指数 ( BMI ) 作 为新的特征参数加入到模型进行训练和测试 。经过不同 人群的多次实验对比, 发现基于 Stacking 集成机器学习 模型对于肥胖人群的血压测量结果有效改善了原有算法 对肥胖人群血压测量准确度不高的问题, 且其误差 MAE/ RMSE 均符合 AAMI 国际电子血压计标准 。对于非肥胖人 群, 本研究显示, 基于 Stacking 集成机器学习模型效果 不显著, 应用价值不大 。下一步的工作方向是建立更为 广泛的 PPG 信号数据集, 进一步对模型进行优化, 构建 一个适合所有肥胖人群的血压测量模型。
参考文献:
[1] 陶然,徐燕, 苏健,等 . 成人肥胖测量指标与高血压患病关系[J]. 实用老年医学,2014.28(11):902-905.
[2] Martina J R, Westerhof B E, Goudoever J V, et al. Noninvasive Continuous Arterial Blood Pressure Monitoring with Nexfin (R) [J]. Anesthesiology, 2012(5):1092- 1103.
[3] Chye L Kho,Mark A Brown,Sharon L H Ong,et al. Blood pressure measurement in pregnancy: the effect of arm circumference and sphygmomanometer cuff size[J]. Obstetric Medicine, 2009. 2(3): 116- 120.
[4] Taha Z, Shirley L, Razman M. A review on non-invasive hyper ‐ tension monitoring system by using photoplethysmography meth ‐ od[J]. Movement, Health & Exercise, 2017. 6(1).
[5] F Miao, Fu N, Zhang Y T, et al. A Novel Continuous Blood Pres ‐ sure Estimation Approach Based on Data Mining Techniques[J]. IEEE Journal of Biomedical and Health Informatics, 2017. 21(6): 1730- 1740.
[6] Khalid Syed Ghufran,Zhang Jufen,Chen Fei,et al. Blood Pressure Estimation Using Photoplethysmography Only: Comparison be ‐ tween Different Machine Learning Approaches. [J]. Journal of healthcare engineering,2018: 1548647.
[7] Wang L , Wei Z , Ying X , et al. A Novel Neural Network Model for Blood Pressure Estimation Using Photoplethesmography with ‐ out Electrocardiogram[J]. Journal of Healthcare Engineering, 2018:1-9.
[8] 吴绍武,续育茹 . 基于 LightGBM 的血压测量方法研究[J]. 生物 医学工程研究,2019.38(3):312-315.
[9] 贺楚芳 . 基于 PPG 形态学的无创连续血压测量算法研究[D]. 北京:北京交通大学,2020.
[10] 徐海,厚磊,左惠娟,等 . 不同电子血压计测量肥胖人群血压的 准确性[J]. 中华高血压杂志,2017.25(4):338-344.
[11] Saeed M , Villarroel M , Reisner A T, et al. Multiparameter Intel ‐ ligent Monitoring in Intensive Care II: a public-access intensive care unit database.[J]. Critical Care Medicine, 2011. 39(5):952.
[12] 柴川页, 管琦,赵帆帆 . 可穿戴式血压连续测量系统的实现方 案研究[J]. 当代经济,2018(13):129- 131.
[13] 刘艳萍,李杰,金菲 . 基于 RNN 的脉搏波血压计的研究与实现
[J]. 电子技术应用,2018.44(6):76-79.
[14] Lee Chungkeun, Sik Shin Hang, Lee Myoungho. Relations be ‐ tween ac-dc components and optical path length in photople ‐ thysmography[J]. Journal of biomedical optics, 2011. 16(7): 077012.
[15] 陈绍荣,刘郁林,朱行涛,等 . 切比雪夫Ⅱ型模拟高通滤波器的 设计及实现[J]. 通信技术,2020.53(4):806-815.
[16] 赵德康,张永建,路开放 . 脉搏波信号的血压提取算法研究[J]. 现代电子技术,2021.44(6):12- 15.
[17] 张笑东 . 无创血压连续测量技术研究[D]. 沈阳:中国科学院研 究生院(沈阳计算技术研究所),2016.
[18] 曹子轩,尹钟, 张建华 . 基于 Stacking 模型融合策略的脑力负 荷等级评定方法[J]. 软件导刊,2020. 19(1):80-83.
[19] Singh, A, Halgamuge, et al. Impact of Different Data Types on Classifier Performance of Random Forest, Naive Bayes, and K- Nearest Neighbors Algorithms[J]. Int J Adv Comput Sc, 2017.
[20] Muhammad Waseem Ahmad,Jonathan Reynolds,Yacine Rezgui. Predictive modelling for solar thermal energy systems: A com ‐ parison of support vector regression, random forest, extra trees and regression trees[J]. Journal of Cleaner Production,2018:203.
[21] Qi M. LightGBM: A Highly Efficient Gradient Boosting Decision Tree[C]// Neural Information Processing Systems. Curran Associates Inc.,2017.
[22] 周钢 , 郭福亮 . 集成学习方法研究[J]. 计算技术与自动化 , 2018.37(4):148- 153.
[23] Schober Patrick, Vetter Thomas R. Linear Regression in Medi ‐ cal Research.[J]. Anesthesia and analgesia,2021 (1):108- 109.
[24] Charbonnier F M .AAMI/ANSI standard for automatic or adviso ‐ ry external defibrillators. Association for the Advancement of Medical Instrumentation. American National Standards Institute. [J]. Journal of Electrocardiology, 1993. 26 Suppl(Suppl):147.
关注SCI论文创作发表,寻求SCI论文修改润色、SCI论文代发表等服务支撑,请锁定SCI论文网!
文章出自SCI论文网转载请注明出处:https://www.lunwensci.com/ligonglunwen/59308.html