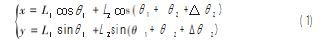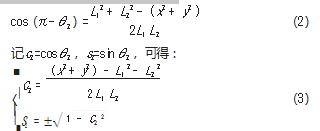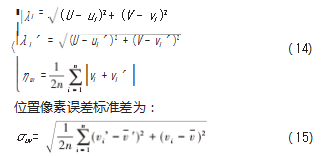SCI论文(www.lunwensci.com)
摘要:为提高 SCARA 机器人的精度, 以 SCARA机器人的零点标定方法为研究对象, 校正因机械加工误差 、装配间隙误差和零件磨损等因素造成实际臂长与设计臂长的偏差, 还有因 SCARA 机器人的大小臂没有完全重合在一条直线上造成实际零点位置与理论 位置的偏差 。通过相机和图像识别技术, 精确地定位出标定器上两个辅助点的位置, 依据 SCARA 机器人的正反解和两点法标定的 方法, 以此标定出零点的实际位置和机器人大小臂的实际长度 。所提出的 SCARA 机器人零点标定方法操作简单, 精度较高, 与一 般的零点标定方法相比, 该方法不需要依靠昂贵的设备, 能满足大部分情况下机器人的工作要求 。 实验结果表明, 经过标定后, 机器人的位置误差在 0.06 mm 以内, 大臂的长度误差在 0.03 mm 以内, 小臂的长度误差在 0.025 mm 以内。
关键词 :零点标定,机械人标定,视觉测量,SCARA机器人
A SCARA Robot Calibration Method Based on Vision Measurement
Wang Wenshuang1. Yao Shujie2. Zeng Yu1. Xie Qixuan2
( 1. Guangzhou Intelligent Equipment Research Institute Co., Ltd., Guangzhou 510530. China;
2. College of Engineering, South China Agricultural University, Guangzhou 510642. China)
Abstract: In order to improve the accuracy of SCARA robot, the zero calibration method of SCARA robot was taken as the research object to correct the deviation between the actual arm length and the design arm length caused by machining error, assembly clearance error and part wear, as well as the deviation between the actual zero position and the theoretical position caused by the incomplete reconnection of the large and small arms of the manipulator. The positions of the two auxiliary points on the calibrator were accurately located through the camera and image recognition technology. According to the positive and negative solution of SCARA robot and the calibration method of two-point method ,the actual position of the zero point and the actual length of the manipulator were calibrated . The experimental results show that the method can effectively improve the accuracy of the robot. After calibration, the position error of the robot is less than 0.06 mm, the length error of the boom is less than 0.03 mm, and the length error of the jib is less than 0.025 mm.
Key words: zero calibration; robot calibration; visual measurement; SCARA robot
引言
SCARA 机器人在生产过程中, 不可避免地存在机械 加 工 误 差 。 此 外, 在 装 配 、 维 修 和 长 时 间 使 用 后, SCARA 机 器 人 还 会 产 生 杆 件 变 形 、磨 损 、 间 隙 等 问 题 。 这 些 问 题 都 会 导 致 SCARA 机 器 人 的 参 数 发 生 变 化, 影响 SCARA 机器人的精度, 使 SCARA 机器人无法 完成精准的操作任务 。为了提升末端执行器位姿的控 制精度, 使 SCARA 机器人能够正常工作, 不得不重新 进行标定, 确定 SCARA机器人的零点位置和大小臂的 实际长度 。
何沁珊等[1]采用定位销的方式将大小臂固定理想位 置来完成零点标定, 该方式操作简单方便, 但精度不高。 许允斗等[2]做了 2RPU/UPR+RP过约束混联机器人零点标 定和全标定理论研究, 有效提高混联机器人的定位精度, 但必须借助激光跟踪仪这种高精度的测量设备 。梅江平[3]等提出了一种基于末端转角误差信息的快速零点标 定方法, 该零点标定方法的鲁棒性好, 准确性高, 但该 方法只适用于并联机器人 。潘伯钊等[4]采用激光三坐标 测量装置对机器人进行标定, 该方法得到的精度较高, 但设备价格昂贵 。郎需林等[5]通过多点法计算零点的位 置, 但计算过程复杂, 实现起来比较困难。
SCARA 机器人的零点标定已经存在比较成熟的技 术和研究, 但是大多数的标定方法都需要借助一些昂贵 的仪器, 且操作过程十分复杂和繁琐, 需要专业的人员 才能完成工作, 使用起来十分不方便 。本文在前人研究 的基础上, 提出了一种简单, 实用的 SCARA 机器人零 点标定方法, 用于解决 SCARA 机器人标定过程中存在 的问题 。该标定方法具有操作简单 、设备便宜 、精度高 的优点, 能满足绝大部分情况下 SCARA 机器人的工作 要求。
1 算法原理
1.1 SCARA机器人运动学正解
如图 1 所示, 在基坐标原点 O 处建立机器人的基坐 标系 xoy, OA 为机器人的大臂, 长度为 L1. OB 为机器人 的小臂, 长度为 L2 。点 O 和A在机器人的关节处, B 与机 器人的末端重合 。末端处点 B 的 x轴坐标值为向量 OA 与 向量 AB在 x轴上的投影之和, y轴坐标值为向量 OA 与向量AB在 x轴上的投影之和, 故有:
式中: θ 1 为 x轴与 OA 的夹角; θ2 为 OA 与 AB 的夹角; Δθ2 为机器人大臂与小臂的理论值与实际值的角度偏差。
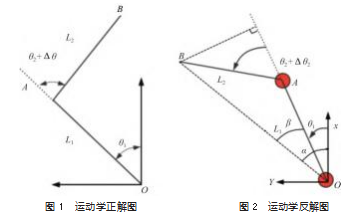
1.2 SCARA机器人运动学反解
如图 2所示, 建立机器人的基坐标系 xoy, 连接 OB, 过点 B 做 OA 的垂线 BC, 交 OA 于点 C。在直角三角形 OBC 中, 根据余弦定理, 可得:
机器人处于右手系时, S2 取正值; 机器人处于左手系, S2取负值, 特别的, 机器人处于奇异位置时, 则S2=0.
根据式 ( 3), 可求得 θ2:
本文约定, 当 θ2 ∈ ( 0. π) ⋃ (−2π, −π) 时机器人 处于右手系; 当 θ2 ∈ ( −π, 0) ⋃ (π, 2π) 时, 机器人 处于左手系 。特别地, 当 θ2 ∈{−2π, −π, 0. π, 2π}, 机器人处于奇异位置。
1.3 误差分析
机器人误差的主要来源为几何误差, 即在机器人的 制造与装配过程中, 由于装配体本身存在间隙误差, 装 配精度低, 机械加工误差, 或长时间使用导致的零件磨 损等因素, 致使 SCARA机器人的大臂关节轴线的位置和 小臂关节轴线之间的相对位姿关系产生误差 。一般通过 提高加工与装配的精度来尽量避免这样的几何误差, 但 是由于数控加工机床本身加工精度以及不可避免的人工 操作误差, 这种方法显然不能完全避免这样的误差 。所 以, 需要通过零点标定的方法来提高 SCARA机器人的精 度, 即首先找出关键的几何误差参数, 然后通过运动学 标定方法求出参数实际值。
SCARA 机器人共有 4个轴和 4个运动自由度, 其中 有 3个旋转关节, 其轴线相互平行, 在平面内进行定位 和定向 。另一个关节是移动关节, 用于完成末端件在垂 直于平面的运动, 即包括绕 X、Y、Z轴的旋转和沿 Z轴 的平移自由度 。其中大臂与基底的装配和磨损导致两臂 轴线不完全重合所造成的误差, 可由大臂长度进行补偿, 垂直移动关节与小臂轴线不完全重合所造成的误差对零 点位置的影响较小, 可以忽略不计 。其他的误差则由前 面所得公式求出。
根据前文所求出的 SCARA 机器人正解公式 ( 1) 和 反解公式 ( 6), 可知机器人的几何误差主要包括大臂长 度 L1 的误差, 小臂长度 L2 的误差和大小臂之间实际值与 理论值的角度偏差 Δθ2.
1.4 零点和臂长的标定步骤及原理
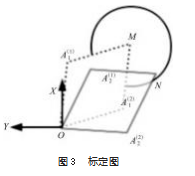
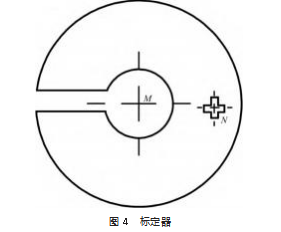
如图 3 所示, 建立SCARA 机器人的基坐标系 xoy, 其中, 点 O 与机器人的基坐标系的原点重 合 。M 、N 为 标 定 器上的两个辅助点, 他们分别为图 4 中标定器上的 圆 形 和 十 字 形 的 中点 。A1 ( 1) 、A1 ( 2) 为相机图像中点与点 M从两个不同方向完全重合时, 机器人大 臂和小臂的交点。标定步骤如下。
( 1) 标定器固定在机器人末端上, 拖动机器人, 使 点 M与相机的中心点重合, 并记录下此时两个关节的角 度 θ1), θ2)。
( 2) 机器人从另一个方向对准相机, 使点 M与相机 的中心点重合, 记录两个关节的角度 θ1), θ2)
( 3) 以同样的方法, 使点 N 与相机的中心点重合, 并对关节角度进行记录, 得到 θ3), θ), θ4), θ)。
根据上述步骤在点 M得到的关节角度和式 ( 1), 可 得到以下方程组:
1.5 误差估算
圆柱形标定器的示意图如图 4所示, 其半径的大小 为 R, 点 M 为标定器上圆形模板的中点, 点 N为十字形 模板的中点。
误差测量步骤如下。
( 1) 将相机摆放到机器人活动范围内下方的任意 位置。
( 2) 调整相机方向, 使相机成像平面与标定器底面 平行。
( 3) 调整相机位置, 使点 M 与成像平面的中心点( U, V) 重合。
( 4) 以 r 为半径, 机器人带动标定器绕成像平面的 中心点画圆, 并记录下 n 个点在图像坐标系下的坐标 ( ui, vi ) 和在基坐标系下的坐标 ( xi, yi )。
( 5) 在另一个手系下, 根据矫正后的角度和运动学 反解, 机器人运动到 ( xi, yi ), 记录下对应 n个点在图像 坐标系下的坐标 ( ui ´, vi ´)。根据上述步骤中, 可得机器人的位置像素误差平均 值为:
在相机坐标系下, 标定器半径在视野内 u 方向上占据的像素长度为 Lu, 在 v方向上占据的像素长度为 Lv, 则可得平均像素当量:
2 实例验证
本 文 采 用 SCARA 机 器 人 进 行 实 验 。 图 5 所 示 为 SCARA 机器人和实验平台, 图 6所示为装在机器人末端 的标定器 。实验所用机器人的大臂设计长度值为 350mm,小臂设计长度值为 250 mm 。所用相机为迈德威视的工业 相机, 分辨率为 2 448×2 048 。实验过程中, 让相机镜头 向上, 与机器人移动轴上的标定器平行, 成像平面的中心 点与第四轴的中心在一条直线上 。相机的固定台保持不 动, 以此保证相机不会发生空间位移。通过调整光源增加 相机的亮度, 来提高标定器上两个图形与背景的对比度。
实验利用德国 MVtec 公司开发的 HALCON 机器视觉 算法包进行二次开发, 根据 HALCON 中的模板匹配算法 开发出一个识别软件, 来识别图中标定器的圆形中点和 十字形中点, 用以作为辅助零点标定的特征点 。识别前, 需要准备从标定器原图上截下来的两种特征图形的图片, 或从原图中将两种特征框选出来 。识别过程中, 将固定 在机器人垂直移动轴上的标定器移动到图像中, 即可将 特征框选出来, 并标记其中心点作为辅助标定的特征点。 移动 SCARA 机器人, 使标定器发生旋转时, HALCON 机 器视觉算法包的模板匹配算法也能精确识别出标示形状 及其中心点, 完成辅助标定的任务。
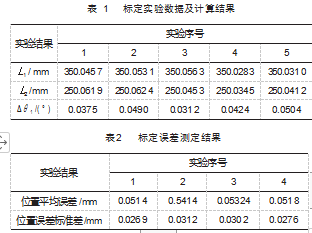
根据前文所述的零点和臂长标定步骤以及误差估算 方法, 对 SCARA 机器人进行标定。测试结果如表 1 所示。
3 结束语
本文针对 SCARA 机器人的精度问题, 以 SCARA 机器人的零点标定方法为研究对象, 根据机器人的正反解 公式, 分析了其误差源参数, 建立其零点标定的方程, 以此对 SCARA机器人进行了零点标定 。提出了零点标定 的视觉测量原理, 搭建了标定实验平台, 得到了实验所 用机器人的大臂长度误差参数, 小臂长度误差参数, 以 及它们之间的角度误差参数的真实值, 并计算了 SCARA 机器人的定位精度误差。
从实验结果来看, 经过零点标定之后, 所用 SCARA 机器人的位置误差控制在了 0.06 mm 以内, 大臂的长度 误差在 0.03 mm 以内, 小臂的长度误差在 0.025 mm 以内, 标定精度较高, 达到了一般情况下 SCARA 机器人的工作要求。
综上所述, 相对于传统的标定方法需要昂贵的测量设备, 且标定过程复杂, 本文所提出的方法具有测量仪 器简单 、操作流程简易 、适用范围广等优点, 便于在工 业上的应用。
参考文献:
[1] 何沁珊, 向中凡,丁声雷 .SCARA 机器人零点标定[J]. 煤矿机械, 2017.38(11):106- 107.
[2] 许允斗,王超,赵春霖,等 . 2RPU/UPR+RP 五自由度混联机器人 参数标定研究[J]. 光学精密工程,2020. 28(1):119- 129.
[3] 梅江平,贺媛,臧家炜 . 基于末端转角误差的并联机器人零点 标定方法[J]. 机器人,2018.40(5):685-692.
[4] 潘伯钊, 宋轶民,王攀峰,等 . 基于激光跟踪仪的混联机器人快 速零点标定方法[J]. 机械工程学报,2014.50(1):31-37.
[5] 郎需林, 张华杰,刘培超,等 .SCARA 机器人机械参数的标定方 法装置及 SCARA 机器人:CN111113419A[P]. 2020.
[6] 赵彬,刘振宇,邹风山,等 . 单臂 SCARA 真空手运动学建模与仿 真[J]. 机械设计与制造,2014(8):183- 185.
[7] 郭晓彬,杨基鹏,石廷亮 . 一种实用的 SCARA 机器人零点及臂 长标定方法[J]. 伺服与运动控制,2018(2):128- 132.
[8] 张皓钧 . SCARA 机器人运动学参数与视觉标定研究[D]. 哈尔 滨:哈尔滨工业大学,2013.
[9] 杨丽红,秦绪祥,蔡锦达,等 . 工业机器人定位精度标定技术的 研究[J]. 控制工程,2013.20(4):785-788.
[10] 王东署 . 工业机器人标定技术研究[D]. 沈阳:东北大学,2006.
[11] 董慧颖,李文广 . 一种基于平面精度的机器人标定方法及仿 真[J]. 中国机械工程,2011.22(17):2039-2042.
[12] Albert Nubiola,Ilian A Bonev. Absolute robot calibration with a single telescoping ballbar[J]. Precision Engineering, 2014.38(3): 472-480.
[13] 吴江杰, 陈伟庆,辛天飞 . 激光干涉仪测量数控机床定位精度 的方法研究[J]. 工业控制计算机,2017.30(11):159- 160.
关注SCI论文创作发表,寻求SCI论文修改润色、SCI论文代发表等服务支撑,请锁定SCI论文网!
文章出自SCI论文网转载请注明出处:https://www.lunwensci.com/ligonglunwen/59233.html