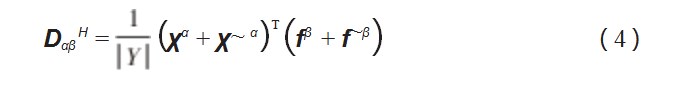SCI论文(www.lunwensci.com)
摘要:点阵材料是一种新兴的轻质高强的材料,由于其具有多尺度特征,采用离散模型需要对所有板杆进行建模和网格划分,导致频率分析费时。常采用均匀化后的等效模型进行分析。主要对等效模型进行频率分析,讨论点阵材料各参数对频率的影响。以一块四边固支的仅具有面内周期性的点阵板为研究对象,分别使用离散模型和三维周期性材料均匀化等效模型、周期性板结构的均匀化等效模型,开展周期性点阵板结构的固有频率的计算,分别改变点阵板的单胞内部参数、单胞的排布个数、单胞的构型,讨论这些因素对固有频率的影响。进而,以离散模型的结果为基准,对等效模型的求解结果进行误差分析,结果显示针对具有面内周期性的点阵板结构,Mindlin等效板模型预测的固有频率误差较小。
关键词:点阵板;渐近均匀化;频率分析
Error Analysis of Equivalent Model of Natural Frequency of Lattice Plate Structure
Liu Shuai1,Yang Rui1,Ji Bin2,Niu Bin 1
(1.School of Mechanical Engineering,Dalian University of Technology,Dalian,Liaoning 116024,China;
2.Shanghai Institute of Aerospace Systems Engineering,Shanghai 201109,China)
Abstract:Lattice material is a new kind of lightweight and high-strength material.Due to its multi-scale characteristics,it is time-consuming to conduct frequency analysis using discrete finite element model,which models and meshes all the plates and rods.The homogenized equivalent model is often used for analysis.The frequency of the equivalent model was mainly analyzed and the influence of the parameters of the lattice material on the frequency was discussed.Taking a lattice plate clamped at four edges with only in-plane periodicity as an example,the natural frequency of the periodic lattice plate structure was calculated using the discrete model,the three-dimensional periodic material homogenization equivalent model and the periodic plate structure homogenization equivalent model.By changing the internal parameters of the unit cell,the arrangement of the unit cell and the cell configuration respectively,the effects on the results were discussed.Then,based on the results of the discrete model,the error analysis of the solution results of the equivalent model was carried out.The results show that for the lattice plate structure with in-plane periodicity,the error of the natural frequency predicted by the Mindlin equivalent plate model is small.
Key words:lattice plates;asymptotic homogenization;frequency analysis
0引言
点阵材料结构有着高比强、高比刚、孔隙率高等一系列优点[1],但由于具有多个尺度,使用离散模型进行分析比较费时,计算困难。所以,将点阵结构等效,使用等效性能进行力学响应的求解就显得尤为重要。
对于点阵材料结构的等效性能求解,许多学者提出了一系列方法,比较常见的是代表体元法[2]、多尺度有限元法[3]、渐近均匀化法[4]。其中,渐近均匀化方法有严谨的数学理论的支撑,以摄动理论为基础,通过对定义在单胞上的偏微分方程组进行求解,获得点阵材料的等效性能。Hassani等[5-6]从理论和数值求解角度对渐近均匀化方法进行了详细综述。然而,均匀化方法的数学属性比较强,对于没有很强的数学背景的设计者来说,使用起来比较困难。对此,Cheng等[4]提出了渐近均匀化方法的新求解方法(New Implementation of Asymptotic Homogeniza⁃tion,NIAH),可以快速计算出三维周期性材料的等效本构矩阵。在此基础之上,Cai等[7]和Yi等[8]受到启发,对NIAH进行推广,分别研究出了周期性板结构的渐近均匀化方法的新求解方法和周期性梁结构的渐近均匀化方法的新求解方法。Zhao等[9]基于NIAH方法研究了了具有随机夹杂聚合物PVC/ABS/nano-CaCO3的等效性质。Zhang等[10]基于NIAH研究了周期性复合材料的等效热膨胀系数。
本文首先介绍渐近均匀化的基本理论,使用离散模型和三维周期性材料均匀化等效模型、周期性板结构的渐近均匀化等效模型,分别改变单胞内部参数、单胞排布个数、单胞构型,开展点阵板的固有频率分析研究。以离散模型的结果为基准,对等效模型的求解结果进行误差分析。
1渐近均匀化基本理论
1.1三维周期性材料的渐近均匀化
渐近均匀化可用于求解周期性材料的等效性能。通过三维周期性材料的渐近均匀化方法,可将微观上材料分布不均匀的三维周期性材料等效为一种均质的材料,求解出该材料的等效本构矩阵CH,并且有下式成立:
1.2周期性板结构的渐近均匀化法
通过周期性板结构的渐近均匀化法,可以将仅有面内周期性的点阵材料结构等效为均匀的板。等效模型有2种,Kirchhoff板模型和Mindlin板模型。其中,Kirch⁃hoff板是比较经典的板模型,假设变形前垂直于中面的直线段变形后仍垂直于中面。而Mindlin板模型打破了这一假设,假设变形前垂直于中面的直线段变形后可以不垂直于中面。这是两种模型的最主要的区别。
与三维周期性材料的渐近均匀化相比,周期性板结构的渐近均匀化求解等效刚度的过程可以分为以下3步[12]:第一步,要先求解单胞在单位位移场作用下的节点力fα(α=1,2,…,6);第二步,把节点力向量作用到单胞上,施加位移周期边界条件,求解特征位移场χ~α(α=1,2,…,6);第三步,求解单胞在特征位移场作用下的节点反力f~β(α=1,2,…,6)。最后,将得到的数据代入到式(4),即可得到单胞的等效本构矩阵:
在实际工程领域当中,由于轻量化要求,结构在大多情况下并不是用实心材料制造的,由于有孔隙存在,影响了剪切刚度,抗剪切能力往往相对较弱,此时横向剪切变形大多不可忽略,考虑其等效剪切刚度是很有必要的。此时,一般需要使用Mindlin板模型进行等效[12]。
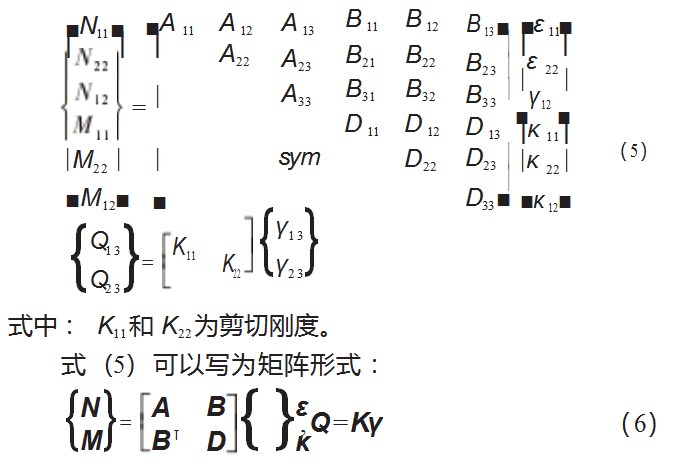
假设它的本构方程为以下形式:
式中:A为面内拉伸刚度阵;B矩阵为拉弯耦合刚度阵;D矩阵为面外弯曲刚度阵;K为剪切刚度阵,可以通过比较宏观板元与微观单胞的内力及外力状态,在单胞上构造与宏观板元一致的应力应变状态,根据宏微观应变能等价求解得到,更多具体细节可以参考文献[12]。
2点阵板固有频率计算和频率误差计算
本章先介绍初始结构,使用离散模型和三维周期性材料均匀化等效模型、周期性板结构的渐近均匀化等效模型,分别改变单胞内部参数、单胞排布个数、单胞构型,开展点阵板的固有频率分析研究。以离散模型的结果为基准,对等效模型的求解结果进行了误差计算。
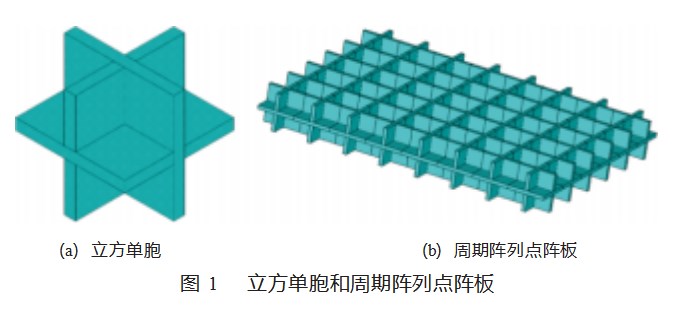
初始结构由立方单胞构成,该单胞由相互正交的3块板组成。为计算方便,假设3块板厚度相同,单胞尺寸为4 cm×4 cm×4 cm。构成点阵的基体材料的弹性模量E=72 GPa,泊松比ν=0.3,密度ρ=2 700 kg/m3。初始结构单胞排布为6×8×1,整体板的尺寸为24 cm×32 cm×4 cm,单胞内面板厚度为0.4 cm,点阵板的边界条件为四边固支。单胞和点阵板示意图如图1所示。
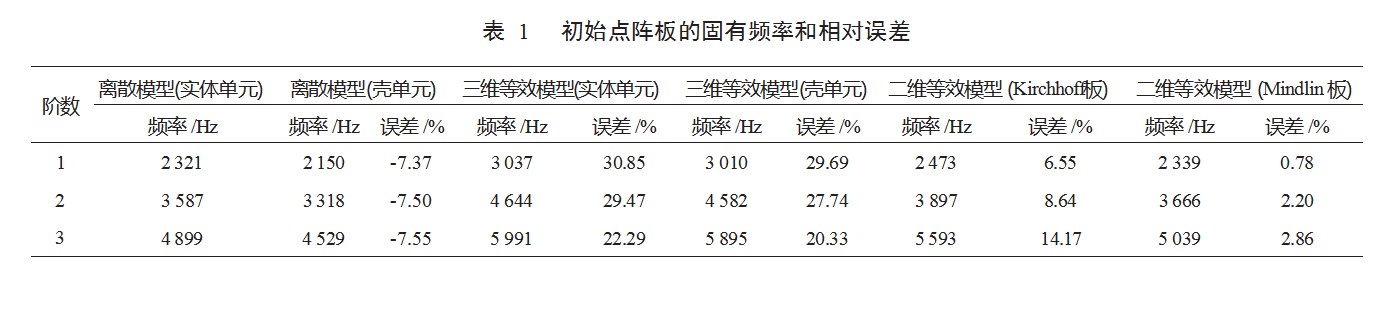
依据单胞构型特点,先分别使用实体单元和壳单元建模进行精确模型计算,随后又分别使用实体单元和壳单元建模进行三维周期性材料的渐近均匀化等效模型计算,最后分别使用等效为Kirchhoff板模型和Mindlin板模型的周期性板结构完成等效计算。随后以实体单元建模的离散模型的结果为基准,对其他模型的结果进行了误差计算。对单胞建模时,使用壳单元时,每个方向10个单元,使用实体单元时每个方向20个单元。三维均匀化时,单元尺寸为0.05 cm。二维均匀化时,面内每个方向10个单元,厚度方向1个单元(后面算例中,如没有特殊说明,则网格数目相同)。前3阶固有频率和相对误差如表1所示。
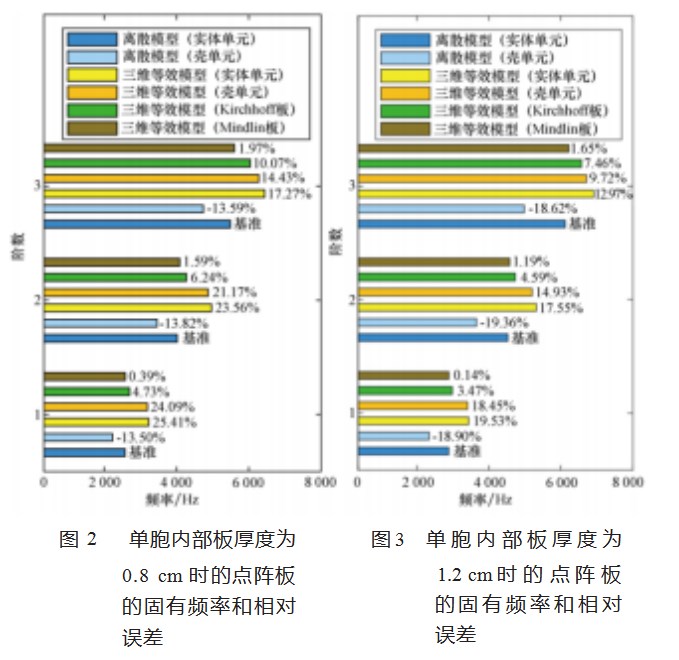
相对于初始结构,仅改变单胞内部的板的厚度,其余不变,对点阵板的前3阶固有频率进行了计算,并进行了误差计算。图2和图3分别是单胞内部板的厚度为0.8 cm、1.2 cm时的计算结果。图中纵轴代表频率的阶数,横轴代表频率,每个柱子后面都有一个注释,标为“基准”的是作为基准衡量其余模型结果误差的频率值,后面标有的数字表示这种模型计算得到的频率的相对误差。
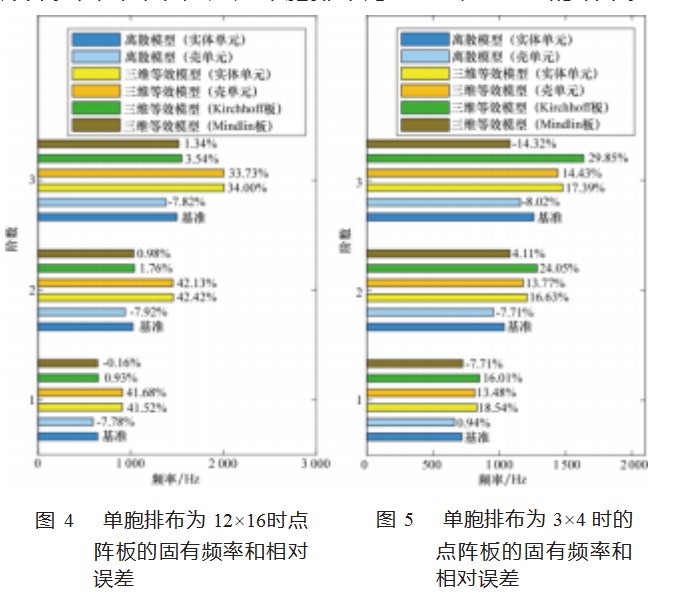
相对于初始结构,仅改变单胞排布数目,其余均不变,对点阵板的前3阶固有频率进行了计算,并进行了误差计算。图4和图5分别是单胞排布为12×16、3×4时的结果。
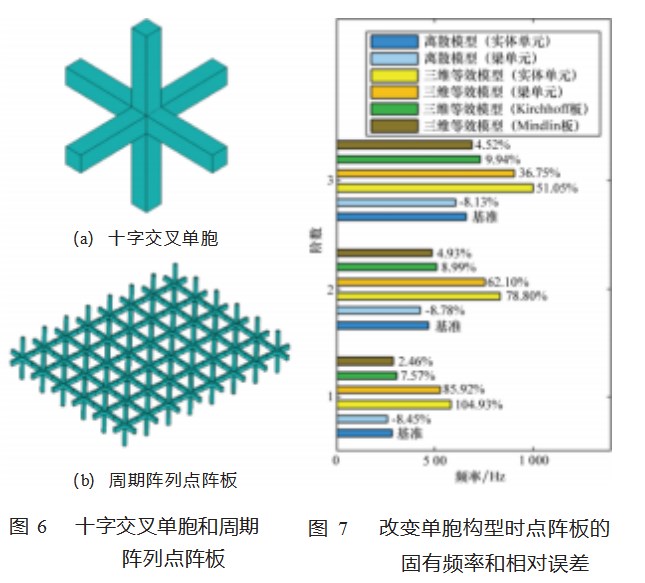
相对于初始结构,仅改变单胞构型,其余不变,对点阵板的前3阶固有频率进行了计算,并进行了误差计算。单胞构型和点阵板示意图如图6所示,该单胞是一种桁架杆单胞,由体心向6个面心连线的6根杆件组成,截面为正方形,尺寸为4 mm×4 mm。离散模型建模时分别使用了实体单元和梁单元,三维均匀化时分别使用了实体单元和梁单元。二维均匀化使用的是实体单元,分别等效为Kirchhoff板模型和Mindlin板模型。对单胞建模时,使用梁单元时,每根杆10个单元,使用实体单元时每个方向20个单元。结果如图7所示。
3结果分析
从点阵板结构不同模型计算的频率误差来看,三维均匀化等效模型的结果误差一般相较于二维均匀化等效模型的误差偏大,这是因为单胞在板的厚度方向只有一层,在这个方向上没有周期性,仅在面内方向有周期性,此时更加符合二维均匀化的使用条件。二维均匀化等效模型的结果中,Mindlin板模型计算得到的结果普遍好于Kirchhoff板模型得到的结果。联合多个不同模型计算的频率误差来看,对于立方单胞,随着单胞内板的厚度增加,使用板单元建模的误差会加大,因而离散板模型的结果的误差也会增大。
总体来讲,结构中单胞数目比较少时,以使用实体单元建模的离散模型的结果为基准,各种等效方法计算得到的误差普遍较大。考虑立方单胞,前3阶频率,单胞排布为3×4时,采用三维周期性材料的渐近均匀化方法的等效模型,其频率最大误差的绝对值为18.54%;采用等效为Kirchhoff板的周期性板结构等效模型,频率最大误差的绝对值为29.85%;采用等效为Mindlin板模型的周期性板结构等效模型,频率最大误差的绝对值为14.32%。当单胞数目比较多时,考虑立方单胞和十字交叉单胞,采用三维周期性材料的渐近均匀化方法等效模型,频率最大误差的绝对值为104.93%;采用等效为Kirchhoff板模型的周期性板结构的等效模型,频率最大误差的绝对值为14.17%;采用等效为Mindlin板模型的周期性板结构等效模型,频率最大误差的绝对值为4.93%,从这些对比可以看出Mindlin等效板模型对固有频率的预测效果更好。
4结束语
本文针对只在面内有周期性的点阵板结构,使用两种离散模型和4种等效模型进行频率分析,讨论了单胞内部尺寸、单胞数目、单胞构型对频率的影响,以实体单元建模的离散模型计算结果为基准,对等效模型计算的频率进行了误差分析。两种离散模型分别是实体单元建模的离散模型和板梁单元建模的离散模型。这4种等效模型分别为使用实体单元建模的三维周期性材料的渐近均匀化等效模型、使用板梁建模的三维周期性材料的渐近均匀化等效模型、等效为Kirchhoff板的周期性板结构的渐近均匀化等效模型、等效为Mindlin板的周期性板结构的渐近均匀化等效模型。得如下结论。
(1)针对点阵板的频率计算,相对于使用三维周期性材料的渐近均匀化等效模型,使用周期性板结构的渐近均匀化等效模型频率计算误差小。
(2)周期性板结构的渐近均匀化法对结构中单胞足够多的点阵板进行等效时,结果比较准确,与此同时,等效为Mindlin板比等效为Kirchhoff板效果更好。结构中单胞数目太少时,误差仍然较大。
参考文献:
[1]杨亚政,杨嘉陵,曾涛,等.轻质多孔材料研究进展[J].力学季刊,2007(4):503-516.
[2]Sun CT,Vaidya RS.Prediction of composite properties from a representative volume element[J].Composites Science and Tech⁃nology,1996,56(2):171-179.
[3]Efendiev Y,Hou T.Multiscale finite element methods for porous media flows and their applications[J].Applied Numerical Mathe⁃matics,2006,57(5):577-596.
[4]Cheng G D,Cai Y W,Xu L.Novel implementation of homogeni⁃zation method to predict effective properties of periodic materials[J].ActaMechanicaSinica,2013,29(4):550-556.
[5]Hassani B,Hinton E.A review of homogenization and topology optimization I-homogenization theory for media with periodic structure[J].Computers and Structures,1998,69(6):707-717.
[6]Hassani B,Hinton E.A review of homogenization and topology op⁃timization II-analytical and numerical solution of homogenization equations[J].Computers and Structures,1998,69(6):719-738.
[7]Cai Y W,Xu L,Cheng G D.Novel numerical implementation of asymptotic homogenization method for periodic plate structures[J].International Journal of Solids and Structures,2014,51(1):284-292.
[8]Yi S N,Xu L,Cheng G D,et al.FEM formulation of homogeniza⁃tion method for effective properties of periodic heterogeneous beam and size effect of basic cell in thickness direction[J].Com⁃puters and Structures,2015,156:1-11.
[9]Zhao J,Li H Y,Cheng G D,et al.On predicting the effective elastic properties of polymer nanocomposites by novel numerical implementation of asymptotic homogenization method[J].Com⁃posite Structures,2016,135:297-305.
[10]Zhang Y C,Shang S P,Liu S T,et al.A novel implementation algorithm of asymptotic homogenization for predicting the effec⁃tive coefficient of thermal expansion of periodic composite mate⁃rials[J].ActaMechanicaSinica,2017,33(2):368-381.
[11]蔡园武.周期性板结构的渐近均匀化方法及微结构优化[D].大连:大连理工大学,2014.
[12]徐亮.周期梁板结构等效剪切刚度的预测及双尺度并发拓扑优化设计[D].大连:大连理工大学,2018.
关注SCI论文创作发表,寻求SCI论文修改润色、SCI论文代发表等服务支撑,请锁定SCI论文网! 文章出自SCI论文网转载请注明出处:https://www.lunwensci.com/ligonglunwen/59214.html