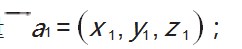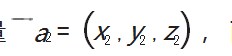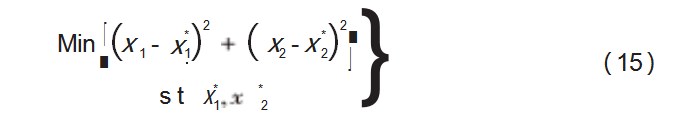SCI论文(www.lunwensci.com)
摘要:针对三坐标测量设备测量机翼缩比模型,大展弦比机翼模型产生大变形时测量点与加载点不统一,加载方向发生变化等问题,从解析几何与有限元角度,开展机翼缩比模型的刚度反求研究。首先,以测量的形变数据与测量点坐标建立面密度函数;然后,通过所提出的实测点回归方法计算实测点的位置坐标信息,再通过坐标信息计算实测点的位移并构造类似有限元的网格结构;将模型按刚心轴简化为悬臂梁,反求悬臂梁的材料属性并计算弹性模型仅在竖直方向力作用下的变形值,从而修正测量数据;最后按照静力等效原则对实际测量坐标下的网格进行等效节点载荷计算,得出模型修正刚度值。经过平板以及变厚度弹性模型有限元验证以及试验分析,结果显示所提出的方法在结构相对变形超过7%时可降低试验误差,为机翼设计制造验证提供数据支持。
关键词:缩比模型;刚度反求;载荷等效;误差修正
Inverse Stiffness Calculation Method of Wing Aeroelastic Scale Model under Large Deformation
Zhao Chuang,Wang Sheng,Liu Guansan,Chi Honggang,Yang Rui
(School of Mechanical Engineering,Dalian University of Technology,Dalian,Liaoning 116024,China)
Abstract:Aiming at the problem that the measuring points and loading points are not uniform and the loading direction changes when the wing scale model is measured by three coordinate measuring equipment and the wing model with large aspect ratio produces large deformation,the stiffness inverse calculation of the wing scale model was carried out from the perspective of analytic geometry and finite element.Firstly,the surface density function was established by measuring deformation data and measuring point coordinates.Then,the position coordinate information of the measured points was calculated by the proposed regression method of measured points,and the displacement of the measured points was calculated by the coordinate information and the grid structure similar to the finite element was constructed.The model was simplified as a cantilever beam according to the rigid center axis to reversely calculate the material properties of the cantilever beam and calculate the deformation value of the elastic model only under the action of vertical force to correct the measurement data.Finally,according to the static equivalent principle,the equivalent node load of the grid under the actual measurement coordinate was carried out to calculate the modified stiffness value of the model.The finite element verification and experimental analysis of the plate and variable thickness elastic model show that the proposed method can reduce the test error when the relative deformation of the structure exceeds 7%,and provide data support for the design and manufacture verification of the wing.
Key words:scale model;inverse stiffness;equivalent load;error correction
0引言
大展弦比机翼在气动载荷的作用下会产生较大的弹性变形。机翼变形后会引起气动变化,导致机翼产生气动弹性效应,对结构安全、稳定性、飞行质量等都将产生重大影响。
采用弹性模型进行风洞试验可以得到飞机的弹性特性,能够准确预测飞机的气动特性,保证飞机的飞行安全。飞机静弹性风洞试验模型一般采用刚性机身和弹性机翼的结构形式,且飞机的静弹性模型与真实飞机的刚度相似。通过测量静弹性模型在静载荷作用下的变形,可以检验静弹性模型与真实飞机的刚度相似性[1]。
静弹性风洞模型的刚度试验是获取弹性模型实际刚度分布与设计刚度吻合程度的重要方法,其结果对静弹性模型设计、风洞试验数据分析具有重要指导意义[2]。而且由于风洞试验成本以及安全性问题,在风洞试验之前也要进行强度和刚度试验以检验飞机的强度以及刚度是否满足要求,防止破坏风洞实验室出现安全问题。
刚度试验比较传统的方法是挂砝码定点加载,如图1所示,采用千分表或三坐标机等测量外部变形,然后依据公式反推出刚度,这种方法精度比较难保证,而且对于大变形工件来说,测量难度较大。为了解决该问题,黄国宁等[3]采用多剖面组合加载方法进行大展弦比机翼刚度试验,有效克服了单剖面加载的弊端,使得试验精度大大提高。张清勇等[4]针对大尺寸三维位移测量的实际情况,开发了位移摄影测量分析系统,可以减少安装、校准等工作量,也能保持更高的测量精度。黄太誉[5]针对飞机强度试验中准确测量三维位移的要求,提出了投影法和等体积法的间接测量三维位移的大变形测量方法,经过试验验证,测量误差可以达到5‰以内,提高了试验位移测量的准确度。
针对刚度试验模型大变形下出现非线性特征,影响试验结果可靠性的问题,目前很多方法都是通过改变加载或者测量方法来降低试验误差,较少从测量数据方面入手,因此,本文考虑从测量数据方向研究降低试验误差的方法。首先获取测量数据与坐标建立面密度函数,计算实测点的位置坐标并构造类似有限元的网格结构;将模型按刚心轴简化为悬臂梁,反求悬臂梁的材料属性,并计算弹性模型在仅存在竖直方向力作用下的变形值,修正测量数据;最后计算出模型修正刚度值并开展试验验证。
1问题及分析
1.1刚度试验原理
模型经过加工必定会存在误差,因此加工完成后需要进行刚度试验以检验模型加工质量。根据刚度系数的定义,刚度系数(或刚度矩阵)实际上是无法测试的,静力试验只能测量结构的柔度矩阵[6](工程中常称之为影响系数矩阵)。
弹性模型的弹性变形和作用力的关系[7]:
1.2刚度试验方法及误差分析
本文中的刚度试验方法是用定量加载系统施加载荷,采用激光位移传感器测量外部变形,加载与测量方向始终垂直于水平面。采用“定点加载,多点测量”的方式进行柔度影响系数测量。通过加载机构对指定点施加指定载荷,在变形情况下测量模型被测点的坐标值,两次测量的差值即为形变值,即可计算模型被测点的柔度系数。
若模型受到的外载荷足够大,会产生大变形,此时模型的变形包含弯曲与扭转变形,再使用上述方法加载会产生误差,这项误差主要分为3部分:(1)加载点不统一,模型大变形导致加载装置中的加载头在模型变形过程中出现滑移产生误差;(2)测量点不统一,模型大变形导致实际测量点偏离原本的测量点产生误差;(3)加载误差,模型变形导致加载方向发生变化产生误差。
为解决该问题,本文提出一种针对特定加载测量方式下测量大变形静弹性模型的刚度试验误差处理办法,通过还原实测点计算出实测点的刚度值,再使用节点载荷等效计算应测点的刚度值,最后通过等效梁的办法降低加载误差的影响。
2面向模型大变形的刚度反求方法
针对上述刚度试验方法引起的3部分误差,对于前两项误差,首先根据测量数据构造面密度函数,通过提出的测量点回归方法提取实际测点基于未变形模型的坐标,再根据实测点与待测点构造包含所有点的区域,利用节点等效原则求解柔度影响系数矩阵。
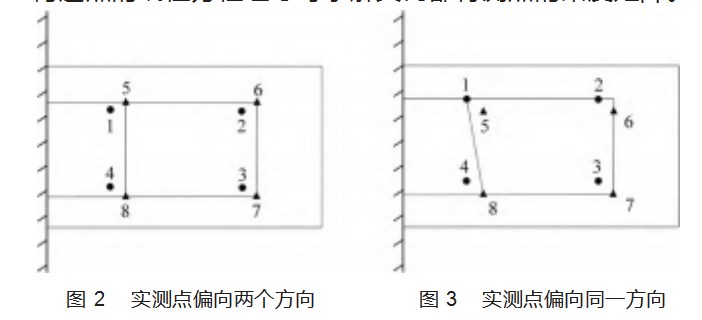
在弹性模型受集中载荷产生形变时,该点会产生两种不同情况的偏移:(1)该点形变后在不同载荷情况下都会偏向同一方向;(2)该点形变后会因载荷施加位置不同而偏向模型内部,如图2~3所示,图中圆点为待测点,三角点为模型形变后对应的实测点。因此构造区域有两种情况:实测点偏向两个方向;实测点偏向同一方向。对于第一种情况,通过实测点构造的区域即可直接求得区域内部待测点柔度矩阵,第二种情况,需要求解构造点的线性方程组才可求解其内部待测点的柔度矩阵。
2.1实测点回归方法
根据测量数据构造面密度函数并得到其表达式f(x,y,z)=0。根据基准位置,采用不断寻求微元法矢方法得到理论测点数据。具体方法:计算模型变形之前曲面上对应测量点的曲线弧长lx(也就是模型实际测点的Y值);以模型根部定位块垂直测量点对应曲线的方向矢量作为初始法向量
再根据向量垂直寻找第一个基向量
两个向量满足如下关系式:
2.2节点载荷等效
求解该问题可得到单元各节点的等效载荷。
2.3等效梁刚度反求流程
针对刚度试验方法引起的加载误差,假设弹性模型为根据刚心轴简化的变刚度梁,通过反求梁的刚度再计算分力Fz单独作用下的变形从而减小加载误差,集中载荷通过建立的面密度函数求导算得。
针对简化后的悬臂梁大变形问题,在弹性模型的加载点端位移未超出中等变形范围(梁长度的10%范围内),运用Awtar等[9]提出的梁约束模型反求梁的刚度,达到或超出中等变形范围,运用陈贵敏等[10]提出的链式梁约束模型基于分段化的思想反求梁的刚度,最后运用链式梁约束模型计算模型仅在竖直方向分力下的变形。
(1)梁约束模型方程
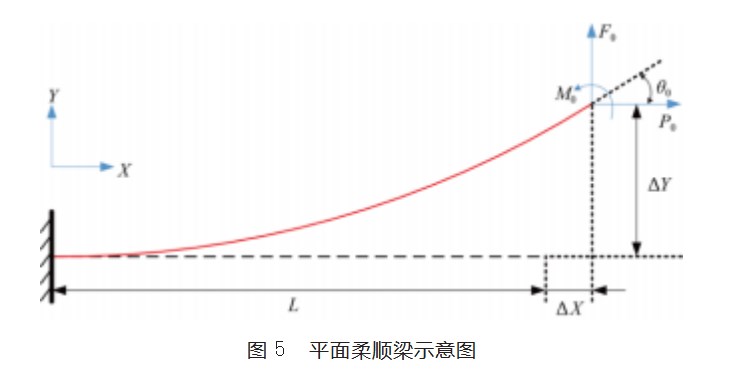
如图5所示,基于Euler-Bernoulli梁假设,可以得到归一化后载荷与形变之间的关系式如下:
(2)分段反求梁刚度流程
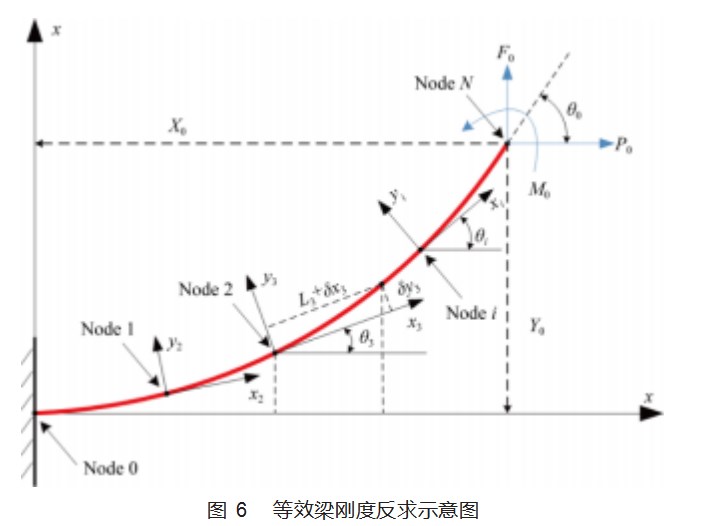
当模型加载处变形处于或超出中等变形范围时,将梁按变形后加载点X坐标分为N段梁,几何关系如图6所示,第一段梁的局部坐标系和全局坐标系重合,因此作用在点1上的载荷可以由末端载荷求出,即
每一段都可按梁约束模型求解,进而采用链式梁约束模型求解仅在F0作用下的加载点末端位移和转角,并修正刚度试验中的测量值。
3模型算例仿真及试验验证
3.1平板模型有限元仿真
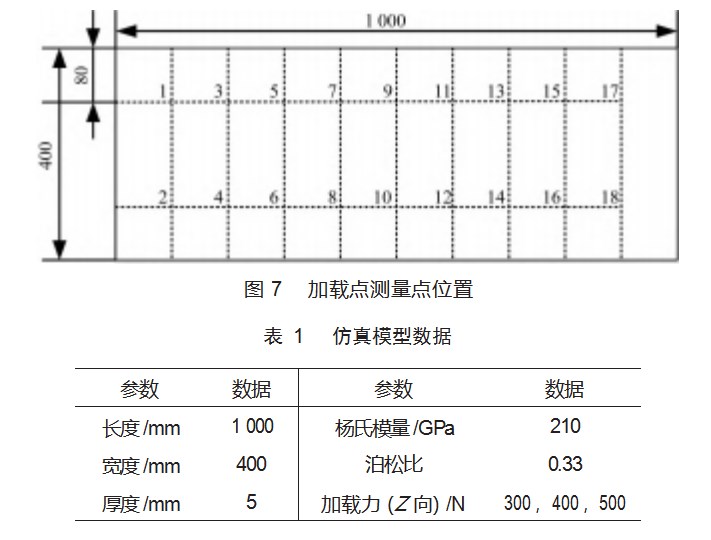
根据本文的刚度求解方法,采用有限元分析软件ANSYS建立平板有限元模型,模型使用壳单元SHELL181建模,边界条件为短边固支,其余边自由,如图7所示,具体模型数据如表1所示。
建模完成后,由于加载方式为定点多级加载,加载位置统一,采用优化反求方法分别求取各级加载力下基于平板坐标系上的最终加载点,优化列示如下:
加载点求得之后,分别于加载点逐级施加载荷并提取测量点位置的位移,根据上述刚度计算方法利用商用软件MATLAB进行平板模型大变形刚度求解,输出刚度矩阵。
3.2变厚度弹性模型有限元仿真
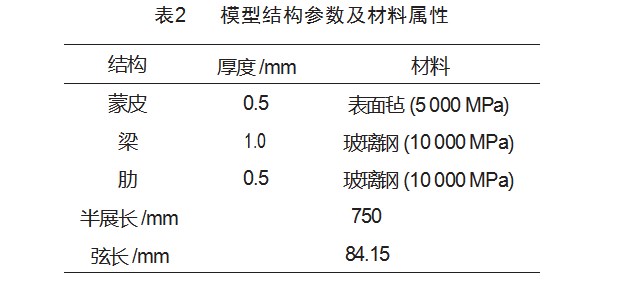
采用有限元分析软件ANSYS建立大展弦比长直机翼简化模型,该模型翼型采用PROFILI软件中的NACA0012翼型,模型梁肋如图8中红线所示分布,整体模型使用壳单元建模,边界条件为一边固支,其余边自由,每点加载力为Z向8.5 N,加载点为梁肋交点,具体模型部分数据如表2所示[11]。
3.3模型试验验证
试验测量仪器采用自行搭建的全自动三维测量与加载设备,静力加载装置由高精度伺服电缸、基于高精度力传感器的闭环反馈控制系统组成;测量系统由三轴运动台、点激光位移传感器等组成。
试验模型使用标准试验件,如图9所示。标准试验件由螺栓固定在支撑平台,工控机根据测量加载点顺序确定加载轨迹;加载设备移动到相应位置,对模型施加200 N力使其产生变形,直到模型稳定;测量设备依照轨迹对模型测点进行测量;测量设备回0,加载设备移动到下一点继续测量直至所有点加载测量结束,并记录数据。
4结果分析
为了验证本文所提方法的正确性,需要对测量柔度矩阵、处理柔度矩阵与理论柔度矩阵进行比较。在结构刚度矩阵中当结点数目较多时,[K]为一个稀疏矩阵,如果使每个单元的两个结点编号差值尽可能小,则非零元素集中在主对角线附近呈带状。因此在判断刚度矩阵是否相匹配时,可以使用刚度矩阵对角线元素的平均偏差系数作为刚度的评定准则,定义测量的模型和理想模型刚度相似的准则如下式所示:
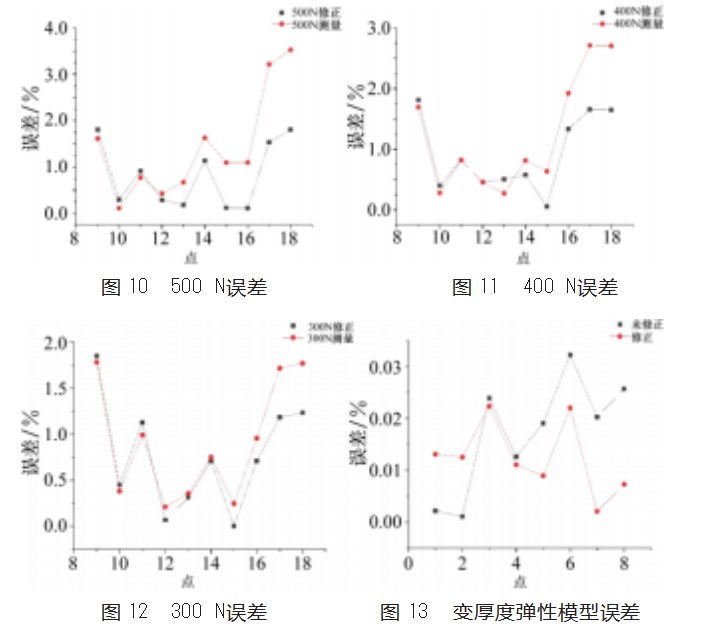
对平板模型仿真结果进行处理后的柔度矩阵对角线数值偏差如图10~12所示。对变厚度弹性模型仿真结果进行处理后的柔度矩阵对角线数值偏差如图13所示。
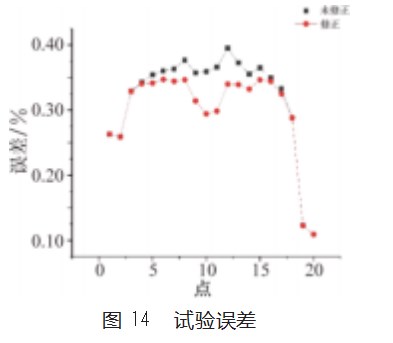
对试验结果进行处理后的柔度矩阵对角线数值偏差如图14所示。分析平板有限元模型以及大展弦比长直机翼有限元模型仿真得到的未修正柔度矩阵与修正柔度矩阵可知,在模型变形较大,约为7%时(图10第12点之后,图11第14点之后,图12第16点之后,图13第4点之后),采用修正方法得到的数据相对误差均小于常规方法计算所得数据的相对误差。在模型变形较小时,由于所提出的实测点回归性方法计算存在一定的误差,与模型变形相比,此误差起主要作用,因此所修正的柔度矩阵误差会比常规方法评定误差较大。
分析试验结果可知,用修正方法所得柔度矩阵与常规方法所得柔度矩阵相比,修正方法所得柔度矩阵更为精确,经过计算,对标准试验件的柔度矩阵修正效果最大为18.35%,位于形变位置最大点,且当弹性模型相对形变大于7%时,应用修正方法得到的柔度矩阵都要更为精确。
测量误差最大达到近40%是因为标准试验钢板本身刚度较小,在加载之前会由于重力影响而弯曲,属于系统性误差,而弹性模型的刚度较大,而且模型重量较小,重力影响对测量精度的影响也较小。
5结束语
本文针对刚度试验测量模型大变形使用常规评定方法所产生的评定误差问题,提出了一种可以降低试验误差的修正方法。对比有限元计算与试验验证的结果,分析了该方法的修正效果,得如下结论。
(1)针对试验中的平板及变厚度模型,结构相对变形较小时(相对展向长度变形不超过7%),应用修正方法得到的柔度矩阵精度并不会提高,因此当弹性模型相对变形较小时,应采用传统处理方法。
(2)结构相对变形较大时,应用修正方法后得到的柔度矩阵更为精确,且变形越大,修正效果越好,这说明结构大变形时应用本文修正方法可以降低前述分析的三部分误差,对平板模型以及变厚度模型都适用。但模型不同,修正效果也不同,因此不同模型之间修正效果并不能定量表示。
参考文献
[1]Liu J,Guo H,Lv B.Technique on Automatic Flexibleness Coeffi⁃cient Measurement System of High-Aspect Ratio Wing[C]//Pro⁃ceedings of the 3rd International Conference on Information Technologies and Electrical Engineering(ICITEE2020).Associa⁃tion for Computing Machinery,New York.New York,ICITEE,2020:93-95.
[2]周栋,吴慧勇.基于杠杆原理的起落架疲劳试验随动加载装置分析[J].飞机设计,2008,28(1):20-22.
[3]黄国宁,洪兆贵,孙晓红,等.机翼刚度试验及数据处理方法研究[C]//第十三届全国空气弹性学术交流会,2013.
[4]张清勇,郭永波,高战朋.摄影位移测量技术在飞机静力试验中的应用[J].测控技术,2015,34(12):26-29.
[5]黄太誉.飞机强度试验大变形位移测量技术研究与应用[J].工程与试验,2018,58(3):13-16.
[6]杨智春,赵令诚.飞行器气动弹性力学[M].西安:西北工业大学出版社,2009.
[7]郑钢.静气动弹性模型的设计和风洞试验[J].飞机设计,2000(2):1-11.
[8]张建刚,孙仁俊,唐长红.大型飞机气动载荷向有限元节点等效分配的方法[J].力学与实践,2017,39(1):25-29.
[9]Awtar S,Slocum A H,Sevincer E.Characteristics of Beam-Based Flexure Modules[J].Journal of Mechanical Design,2007(129):625-639.
[10]Chen G,Ma F,Hao G,et al.Modeling Large Deflections of Ini⁃tially Curved Beams in Compliant Mechanisms Using Chained Beam-Constraint-Model[J].Journal of Mechanisms and Robot⁃ics,2018,11(1).
[11]葛少杰.机翼几何非线性颤振风洞模型设计及地面振动试验[D].大连:大连理工大学,2020.
关注SCI论文创作发表,寻求SCI论文修改润色、SCI论文代发表等服务支撑,请锁定SCI论文网! 文章出自SCI论文网转载请注明出处:https://www.lunwensci.com/ligonglunwen/59212.html