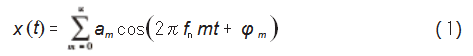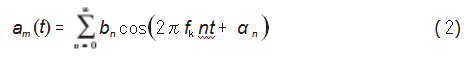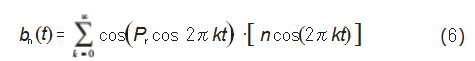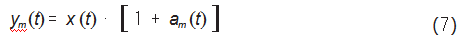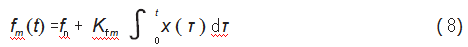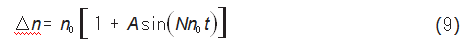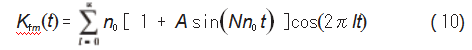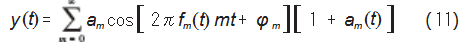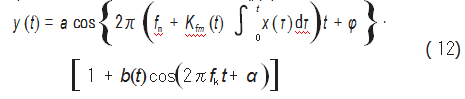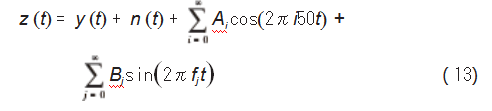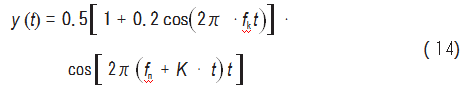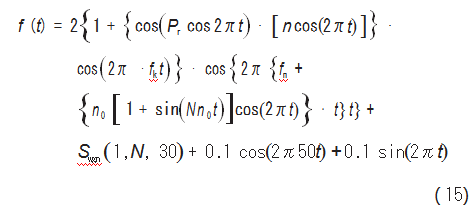SCI论文(www.lunwensci.com)
摘要:滚动轴承是机车车辆走行部的关键部件,其故障概率较大,振动机理复杂,具有非平稳性,故障诊断困难。为解决该问题,从研究机车轴箱滚动轴承故障发生的机理入手,对冲击故障振动信号加以研究。在实际工况下,着重考虑了载荷和工作转速这两个非线性非平稳性因素,并在此基础上建立了机车滚动轴承冲击故障的数学模型。通过所建立的数学模型,对其进行MATLAB仿真信号分析,同时以某大学轴承故障数据集中的外圈故障为例,开展进一步的MATLAB仿真分析,在一定程度上验证了机理分析和所建立数学模型的正确性。
关键词:机车滚动轴承,故障振动机理,非平稳性,数学模型,仿真分析
Analysis on Non-stationary Vibration Mechanism of Rolling Bearing Impact Failure of Locomotive
Wu Bingbing,Wang Jing
(School of Information and Electrical Engineering,Hunan University of Science and Technology,Xiangtan,Hunan 411201,China)
Abstract:Rolling bearings is the key components of the running part of locomotives Its fault probability is large,its vibration mechanism is complex,and it has non-stationarity,so the fault diagnosis is difficult.In order to solve this problem,the impact fault vibration signal was studied by studying the mechanism of locomotive axle box rolling bearing failure.In the actual working condition,the load and the working speed were considered,and on this basis,the mathematical model of locomotive rolling bearing impact fault was established.Through the established mathematical model,the MATLAB simulation signal analysis was carried out.At the same time,the outer ring fault in the bearing fault data set of a university was taken as an example to carry out further MATLAB simulation analysis,which verified the correctness of the mechanism analysis and the established mathematical model to a certain extent.
Key words:locomotive rolling bearing;failure vibration mechanism;nonstationarity;mathematical model;simulation analysis
0引言
在机车运行过程中,轴箱轴承作为机车走行部的关键部件,很大程度上减少了轴与轴之间摩擦带来的损失,对零件之间的运转起到支撑作用,同时具备良好的承载能力。轴承长期工作在强振动、负载不均、温差大、多粉尘的恶劣工作环境中,是走行部中故障率较高的部件。轴箱轴承的主要用途是联系构架和轮对,不同于其他静止机械设备上的轴承元件,它不仅要承受机车静态压力,还要受到运行过程中由径向加速度引起的非稳定动态载荷,车速越高,振动越大,动态压力也越大[1]。轴箱轴承在运行过程中同时受摩擦阻力、负载变化、频繁加减速和装配间隙等非线性因素的影响,因此反映其运行状态的振动信号表现出明显的非线性非平稳性特征,这是机车滚动轴承故障诊断的难点,同样也是当下故障诊断研究的热点。尤其是在实际工况下运行时,轴承故障振动信号的非平稳性愈发明显,对其进行故障诊断十分困难,因此研究其故障发生机理是分析故障原因的重要手段。
近年来,许多学者对轴承的故障机理展开了大量研究,本文参考相关文献对其故障机理进行研究[2-5],针对载荷和工作转速两个非线性非平稳性因素,分析机车轴箱轴承冲击故障信号,确定故障信号类型;在实际工况下,着重考虑载荷和工作转速这2个非线性非平稳性因素,获得机车滚动轴承冲击故障数学模型,进行仿真验证,并将模型应用于实际工况下的轴承故障分析,验证所建立的故障机理模型。
1机车轴箱轴承故障的振动机理分析
1.1机车轴承的故障特征频率
当机车轴承的某个元件发生故障时,故障点与滚动体相互碰撞所产生的频率是不同的,不同的元件有与之相对应的频率。所以,可以根据故障点与滚动体相互碰撞所产生的频率判断发生故障的元件,此频率称为“故障特征频率”。由轴承的转速和零件尺寸可计算具体元件的故障特频率[6],如表1所示。表中:fn为轴承的转动频率,fn=N/60,N为轴承的转速;Z为滚动体的个数;d为滚子直径;D为轴承节径;α为接触角。
1.2故障信号振动机理分析
当轴箱轴承的某一部件出现损伤故障时,提取故障采样振动信号对其进行频谱分析,可以发现频谱图中通常存在以故障点所在部件的故障特征频率为中心频率,以轴承的转动频率围绕其两侧的调制频率的调制边频带;通过已知采样振动信号中提取到的调制信息,分析其频率成分和强度大小,可以初步判断轴箱轴承的故障位置以及故障程度[7]。
1.2.1调幅分析
机车轴箱轴承跟随安装轴转动时,参与滚动的滚动体个数交替变化,其振动信号中一般会存在周期性的瞬态冲击信号。当轴承无故障时,其振动信号的主要成分包含转动频率及其各次谐波频率,正常振动信号x(t)的表达式如下:
式中:am为转动频率第m阶谐波分量的幅值;fn为轴承的转动频率;φm为转动频率第m阶谐波分量的相位。
当轴箱轴承出现损伤类故障时,轴每转一圈,故障点就会和与之相接触的元件表面碰撞一次,故障振动信号的幅值也会产生幅值调制现象,冲击信号的强弱发生周期变化。因此,用am(t)表示幅值调制函数,计算公式为:
式中:bn为幅值调制函数第n阶分量的幅值;αn为幅值调制函数第n阶分量的相位;fk为故障点所在部件的故障特征频率。
但是,机车在实际工况下运行时,受曲线、轨道不平顺等因素的影响,轴箱轴承载荷会发生变化,负载越大,振动信号的幅值越大,而轴箱轴承同时承受径向和轴向的联合载荷作用,因此需将实际工作载荷转换为当量负荷[8],公式如下:
式中:Pr为当量负荷;ha为轴向负荷系数;Gr为轴向轴承的径向载荷;Gv为垂直负荷;GH为水平负荷。
载荷的变化同时也影响着轴承的接触应力和变形。分析滚动轴承的接触应力及变形的难度在于滚动体与圈体的接触。滚动体与内圈是凸面与凸面相接触,滚动体与外圈是凸面与凹面相接触,所以滚动体与内圈的应力集中程度大于滚动体与外圈的应力集中程度,同时内圈接触变形也会大于外圈接触变形[9]。在载荷为0的情况下,滚动体与圈体的接触为点接触,随着载荷的不断增大,点接触变为面接触。当由点接触向面接触过渡时,由于变形较快,接触变形的增量较小;当接触变为面接触时,滚动体与轴承的接触面积基本上不会再发生变化,此时载荷的持续增加会导致接触变形的增量持续增大[10]。接触区域的位置、形状、大小、接触面压力以及摩擦力分布等接触参数随载荷的变化而变化,是典型的边界非线性问题,尤其是在实际的高速工况下,滚动体接触状态复杂,故障机理分析也复杂。
除去载荷的影响,轴箱轴承的工作转速也对振动信号的幅值有一定影响。随转速不断提高,加速度变化极为不稳定,产生越来越大的离心力,导致滚动体与轴承内外圈之间的接触力显著增加,振动信号的幅值也随之增大。记工作转速为n,表达式为:
式中:h1为载荷系数;h2为载荷分布系数;nlim为极限转速。
因此,综合考虑载荷和工作转速这两个影响因素,幅值bn可表示为bn(t)=F[Pr(t),n(t)],则:
故经过幅值调制后的信号模型表示为:
对调幅后的信号模型ym(t)进行傅里叶变换,得到频谱图并进行分析,可以看出信号频谱是以故障特征频率及其倍频为中心,以调制频率及其倍频为间隔而形成的多对调制边频带。机车轴承振动信号在实际运行过程中产生的载波信号和调制信号均属于多频率成分信号,因此通过傅里叶频谱变换会形成许多围绕故障特征频率及其高次谐波两侧的边频带[11]。
1.2.2调频分析
轴箱轴承在振动过程中产生的振动信号受转速波动、负载变化等非线性非平稳性因素影响,使得故障轴承所在轴的转动频率产生一定的变化,进而与故障轴承的故障特征频率发生频率调制现象[12]。因此,用fm(t)表示频率调制函数。
式中:Kfm为调频波瞬时频率相对于fn的偏移,为轴频信号随时间变化的函数。
对于机车轴承,载荷变化的同时不仅影响振动信号的幅值,也会使轴承的转速发生波动,这种转速波动会造成振动信号的调频现象,从而使振动信号的频率发生偏移。因为任何复杂的运动都可以分解为简单运动的组会,所以将轴承转速波动按简谐规律变化处理,记转速波动为Δn,表示为:
式中:n0为平均转速;A为幅值比;N为每周期的波动次数。
所以可将频偏函数Kfm展开为:
因此实际轴承调幅调频振动信号的表达式为:y(t)=F[x(t),am(t),fm(t)],将变化的轴频信号公式(8)代入公式(7),替换轴频信号x(t)中的轴频fn,则:
为简单明了地分析表达式,对于上述调幅调频振动信号,全部取其一阶信号进行分析,则:
在实际运行过程中,传感器测得的振动信号成分十分复杂,不仅包含故障对振动系统产生的冲击信号,还交杂着环境噪声。经进一步分析,其信号中还包含机械系统内部与滚动轴承相连接的其他零部件相互运动和力的作用产生的电磁干扰,该干扰主要是50Hz工频及其高次谐波。在机车运行过程中,轴承还会产生因自身结构、转轴转动等非线性因素引起的额外冲击振动信号。综合上述影响因素,最终机车轴箱轴承冲击故障的振动信号模型表述为:
式中:n(t)为加性高斯白噪声;Ai为第i阶工频分量的幅值;Bj为第j阶额外冲击振动的幅值;fj为第j阶额外冲击振动的频率。
2机车轴箱轴承冲击故障信号仿真分析
2.1冲击故障信号构造与仿真分析
根据前面的分析与推导可知,机车轴箱轴承冲击故障类的振动信号实际上是一种多频率成分的调幅调频信号。针对公式(12),令fk=0.5 Hz、fn=50 Hz、K=5 Hz/s,在忽略其相位的情况下构造出仿真信号:
式中:fk为轴承故障特征频率;fn为转动频率;增量K为当机车出现转速波动时的度量值。
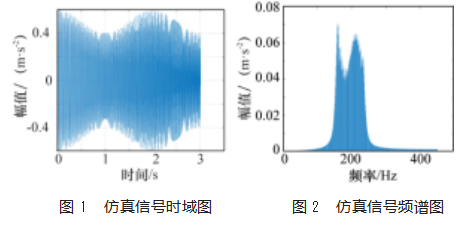
进一步分析仿真信号的频率成分,确定其采样频率fs=300 Hz。因为仿真信号的故障特征频率fk=0.5 Hz,为确保其频谱分析的精准度与清晰度,通过公式Δf=fs/N可计算出其采样点数N为1024。在确定采样频率与采样点数后,对仿真信号进行时域分析,结果如图1所示。由图可知故障特征频率fk与转频信号产生幅值调制的包络线轮廓,同时随着时间不断的增加,转速变大会引发调频现象。
对该仿真信号做频谱分析,结果如图2所示。由图可看到100 Hz等频率成分的转频信号,但由于调频信号与不同时刻的轴频分量相互重叠,造成了谱线模糊,无法确定故障特征频率的存在。
2.2实际工况振动信号仿真分析
根据公式(13)构造实际工况下机车轴箱轴承故障的仿真信号,取Gr=35 kN、ha=1,则Pr=35 kN;取工作转速n=1 200 r/min,平均转速n0=1 000/min,A=1,N=10,令fk=107 Hz,fn=30 Hz,则构造仿真信号为:
式中:Swgn(1,N,30)为环境噪声信号的信噪比为30 dB。
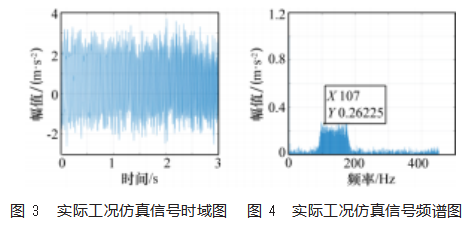
针对实际工况下的振动信号,采取同样的采样频率和采样点数进行时频谱分析,其仿真谱图如图3~4所示。
从图中可知该故障振动信号是周期信号,在故障特征频率fk附近还存在其他较为复杂的谱线,并且该特征频率被环境噪声所湮没,表现出的频率分量较为复杂,很难确定轴承故障类型。
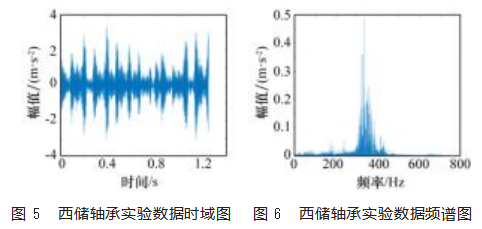
以美国凯斯西储大学故障轴承数据集中的外圈故障为例进行进一步时频谱分析,采样频率为12 000 Hz,采样点数为1 500,理论上的外圈故障频率为107 Hz,仿真结果如图5~6所示。从图中可知实际工况下的振动信号包含更多的环境噪声和其他频率变化因素,信号的频率成分更为复杂,轴承的故障特征频率被噪声所覆盖,但是可以确定其振动信号的周期性及固有频率随其振动幅值而变化,振幅表现出明显的跳跃现象,是明显的非线性振动特征,与仿真信号分析结果一致,进一步验证了故障机理分析的准确性。
3结束语
本文在分析了机车轴箱轴承内圈、外圈、保持架和滚动体故障特征频率的基础上,通过研究机车轴箱轴承的故障振动机理,确定轴承故障振动信号为周期性的调幅调频信号,并对此信号进行数学建模,为诊断轴承故障提供了较为精确的数学模型。同时,通过进一步仿真分析和实验,得知对于机车轴箱轴承故障这类非线性非平稳性振动信号,使用传统的频谱分析方法并不能直接确定其故障类型。在深入研究此故障振动机理的基础上,针对其振动信号的非线性非平稳性特征进行研究,是未来的重点所在。
参考文献:
[1]李永健,刘吉华,张卫华,等.改进样本熵及其在列车轴承损伤检测中的应用[J].仪器仪表学报,2018,39(9):179-186.
[2]OH H,AZARIAN M H,MORILLO C,et al.Failure mechanisms of ball bearings under lightly loaded,non-accelerated usage con⁃ditions[J].Tribology International,2015(81):291-299.
[3]MA Z,DONG S,ZHU H,et al.Research on the failure mecha⁃nism of the high-speed train bearing steel under static load fail⁃ure[J].Engineering Failure Analysis,2022(137):106-169.
[4]杨锦雯.圆柱滚子轴承故障机理与振动特性分析[D].南昌:华东交通大学,2020.
[5]崔玲丽,张宇,巩向阳,等.基于振动响应机理的轴承故障定量诊断及量化分析[J].北京工业大学学报,2015,41(11):1681-1687.
[6]武明泽.基于小波包分解和FPA-SVM的动车组轴箱轴承故障诊断研究[D].北京:北京交通大学,2021.
[7]郭艳平,解武波,龙涛元.拟合故障振动信号模型实现滚动轴承故障诊断[J].机械设计与制造,2017(11):205-208.
[8]杨陈,王辉,沈钢.地铁车辆运行工况对轴箱轴承寿命的影响[J].大连交通大学学报,2015,36(4):32-36.
[9]MEHTA G,SOMANI M,BABU T N,et al.Contact stress analy⁃sis on composite spur gear using finite element method[J].Materi⁃als today:proceedings,2018(5):13585-13592.
[10]王翠翠,陈长征,魏巍.风力机轴承多变载荷下接触应力特性分析[J].噪声与振动控制,2018,38(S1):108-111.
[11]李永焯,丁康,何国林,等.齿轮系统振动响应信号调制边频带产生机理[J].机械工程学报,2018,54(5):105-112.
[12]丁康,孔正国.振动调幅调频信号的调制边频带分析及其解调方法[J].振动与冲击,2005,24(6):9-12.
关注SCI论文创作发表,寻求SCI论文修改润色、SCI论文代发表等服务支撑,请锁定SCI论文网!
文章出自SCI论文网转载请注明出处:https://www.lunwensci.com/ligonglunwen/59081.html