SCI论文(www.lunwensci.com)
摘要 :鞋底模型变形控制是鞋类个性化定制数字化设计的关键技术之一 。针对传统变形方法难以有效地实现鞋底模型个性化定制 变形的问题, 提出一种鞋楦模型数据驱动的分步变形策略, 并基于径向基函数插值实现鞋底模型个性化定制变形的方法 。在鞋楦 模型与鞋底模型的特征提取和位姿匹配完成的基础上, 将级放处理后的鞋底模型变形分为水平维度 、竖直维度 、 内部区域和外部 适应 4 个阶段变形, 分别以鞋楦模型的相关特征作为驱动, 利用径向基函数插值实现鞋底网格模型变形设计 。算法实例表明本方 法能够降低径向基函数插值稳定性依靠形状系数所带来的影响, 有效实现鞋底个性化定制变形, 且变形效果稳定良好 。通过对比 变形前后的随机采样点的间隙余量可以发现, 鞋底模型内部区域较好地适应鞋楦模型曲面特征, 达到个性化定制目的。
关键词:个性化定制,径向基函数插值,鞋底网格模型变形,变形策略
Personalized Customization Deformation of Sole Model Driven by Shoe Last Feature Zhang Yang1. 2. Huang Changbiao1. 2 ※, Zuo Yuanzheng1. 2
( 1. Fujian Key Laboratory of Special Energy Manufacturing, Huaqiao University, Xiamen, Fujian 361021. China;2. Xiamen Key Laboratory of Digital Vision Measurement, Huaqiao University, Xiamen, Fujian 361021. China)
Abstract: The deformation control of sole model is one of the key technologies of the digital design for the personalized customization of footwears. It is difficult to effectively realize the deformation of sole model for personalized customization by means of the traditional deformation methods. A step-by-step deformation strategy driven by the data of shoe last model was proposed . Based on radial basis function interpolation, the method of personalized customization deformation of shoe sole model was realized . Based on the feature extraction and registration of shoe last model and sole model, the deformation of the graded sole model was made up of the deformation of horizontal dimension, the deformation of vertical dimension, the deformation of internal area and the deformation of external area . The deformation was driven by the feature data of shoe last model, and the deformation of the sole model was realized by the radial basis function interpolation . The examples of the algorithm illustrate that the proposed method can reduce the influence resulted from that the stability of radial basis function interpolation depends on the shape coefficient, and can realize the personalized deformation of the sole model effectively and stably . By comparing the gap values of random sampling points before and after deformation, it can be found that the internal area of the sole model can better adapt to the surface characteristics of the last model, so as to achieve the purpose of personalized customization .
Key words: personalized customization; radial basis function interpolation; the deformation of sole mesh model; deformation strategy
引言
研究证明, 足部健康状况与鞋的穿着情况密切相关[1], 而长期穿着不合人脚生理情况的鞋, 既会产生不舒服感又 会严重影响人脚骨骼的发育和成形; 对于有足部疾病的人, 穿着不合适的鞋甚至会恶化其症状。因此针对不同个体的 个性化定制鞋底研究十分具有必要性。传统的个性化定制 方式主要有纯手工定制和基于 CAD/CAM 软件辅助定制等 方式, 这些方式费用昂贵, 效率低下。而数字化设计技术 的发展使得各种个性化定制的成本大大降低, 并使其制作 效率极大提高。在现代社会的主观需求和客观因素的双重 作用下, 针对个性化定制鞋底的研究具有十分重要意义。
个性化定制鞋底主要包括两大流程: ( 1 ) 利用 3D 扫 描技术得到个人的脚部模型, 再提取脚部模型特征数据 驱动标准鞋楦变形获得个性化鞋楦模型; (2 ) 基于个性 化鞋楦模型驱动现有款式的鞋底模型变形获得个性化定 制鞋底模型 。 目前针对鞋底模型变形的研究较少, 绝大 多数的模型变形研究主要围绕模型变形的通用性进行研 究, 针对鞋底模型个性化定制变形可以分为 3 个流程, 分别是特征提取 、模型匹配和模型变形 。在经过特征提 取 、模型匹配后, 鞋楦模型和鞋底模型在空间上满足一 定的位姿约束, 使之符合现实情况的匹配要求, 随后在 此基础之上, 根据鞋楦模型的相关特征对鞋底模型进行变形, 从而达到鞋底个性化定制变形的目的 。本文主要 围绕鞋底模型变形部分开展相关研究, 在完成特征提取 和模型匹配的基础之上, 将径向基函数插值应用于鞋底 模型变形, 并通过变形策略优化径向基函数插值稳定性 问题, 有效实现了鞋底模型的个性化定制变形。
1 相关工作
网格模型的变形一直是研究热点, 并且有了较为成熟的研究成果, 常见的变形技术有空间变形技术 、骨架 驱动变形技术 、多分辨率变形技术以及曲面变形技术等。 空间变形技术的基本原理是将模型嵌入几何空间之中, 然后通过变形函数控制几何空间的顶点移动, 间接 带动几何空间中的模型顶点发生移动, 从而实现模型的 变形[2-3] 。空间变形技术具有操作简便, 灵活性强等优 点, 然而局部区域的变形精度难以控制, 变形较大的场 合容易导致几何细节丢失。
骨架驱动变形技术的基本原理就是为网格模型建立 一个骨架, 并按照一定权重设计把骨架与模型顶点关联 起来, 通过调整骨架位置的方式实现模型变形[4-5] 。骨架 驱动变形技术简单直观, 能够模拟具有骨骼结构的生物 动作, 但是不适合难以建立骨骼结构的模型, 同时对构 建骨架时的权重设置敏感性较强。
多分辨率变形技术的基本原理是将模型分为高频和 低频两部分, 高频部分保存复杂的几何细节, 低频部分 保存简单的全局特征, 变形时针对低频部分进行变形, 保持高频部分不变[6-7] 。多分辨变形技术能够较好地保留 局部细节, 但是处理几何细节较多的复杂模型时, 分解 与重构的工作量巨大, 难以承受。
曲面变形技术的基本原理是从网格模型中选择一部 分区域作为控制区域, 选择一部分区域作为变形区域, 当 控制区域发生变形时, 根据相应的优化目标函数对变形区 域 的 变 形 情 况 进 行 推 导, 从 而 得 出 变 形 区 域 的 形 变 量[8- 10] 。曲面变形技术的操作更加简单直观, 可以直接对 网格模型进行变形操作, 变形精度更高, 其次可以通过约 束来保持局部的几何细节。但是曲面变形技术的缺点是它 们在计算代价和数值稳定性上与网格的复杂度密切相关。
因为空间变形技术变形精度难以控制, 鞋底模型不 适合添加骨架, 多分辨变形技术计算量大, 因此本文采 用了基于径向基函数 (Radial Basis Function) 插值的变 形方法来进行鞋底模型变形, 该方法原理与曲面变形技 术相似, 都是直接对模型进行变形操作, 变形精度较高, 同时径向基函数插值形式简单, 相对于引入各种约束的 曲面变形技术更加简洁, 计算效率更高 。Hardy[11]最早提 出了 Multiquadric 函数, 并将其应用于地貌形状与飞机外 形设计的曲面拟合问题, 标志着径向基函数插值应用的 开端 。现在, 径向基函数插值已经大量的应用于医学图 像的弹性配准, 曲面重建, 人脸变形, 地质学等方面的研究[12- 14] 。 因此, 本文提出了一种基于径向基函数插值 的鞋底模型变形方法, 该方法将径向基函数插值应用于 鞋底模型变形之中, 先根据鞋楦模型相关特征对鞋底模 型部分区域进行变形, 然后使用径向基函数插值拟合鞋 底变形曲面, 从而实现了鞋底网格模型变形 。 同时, 由 于径向基函数作用半径难以确定, 导致径向基函数稳定 性难以保证, 针对径向基函数这一特点以及鞋底模型变 形特点, 本文从变形策略的角度出发, 通过采用合适的变 形策略, 解决径向基函数插值变形方法稳定性不足问题。
2 鞋底变形的前期工作
本文的鞋楦与鞋底模型为 STL 模型, 同时采用了半 边数据结构来构建三角网格模型的拓扑信息。
本文所研究的鞋底模型变形是在鞋楦和鞋底模型特 征提取 、模型匹配的基础上开展的 。因此, 鞋楦和鞋底 模型的相关特征已经提前提取, 鞋楦和鞋底模型的初始 位姿状态也已经提前确定。
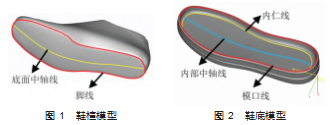
在特征提取部分, 根据鞋底模型变形算法的要求, 针对鞋楦模型, 已经提取了鞋楦脚线 、鞋楦底面中轴线, 如图 1 所示; 针对鞋底模型, 提取了鞋底内仁线 、鞋底模 口线和鞋底内部中轴线等特征, 以鞋底模口线为分界线可 以将鞋底模型划分为内部区域和外部区域, 如图 2 所示。
在模型匹配部分, 已经根据相关约束完成了鞋楦模 型与鞋底模型的位姿调整, 使其符合现实情况下鞋楦和鞋底模型的位姿关系, 并且将鞋楦模型和鞋底模型的长 、宽 、高方向与世界坐标对齐, 使之有了具体的参考方向 。鞋楦模型和鞋底模型的具体位姿关系如图 3 所示。
3 鞋楦特征驱动的鞋底模型变形
本文采用径向基函数插值的方法来进行鞋底变形, 但是, 径向基函数插值方法的稳定性将严重影响变形的精度, 因此, 本文根据径向基函数的特点以及鞋底模型变形的特 点, 从变形策略的角度出发, 通过采用合适的变形策略, 解决了径向基函数插值在鞋底模型变形中所暴露的问题。
直接将径向基函数插值应用于三维空间中, 稳定性 难以保证, 但是将三维模型在二维空间进行变形, 则可 以保证另外一个维度的稳定性, 因此, 本文将鞋底模型的变形拆分为 4 个步骤, 预先统一设定鞋楦与鞋底内部 区域的间隙距离为 t, 依次变形如下: ( 1 ) 水平维度的 鞋底模型变形; (2 ) 竖直维度的鞋底模型变形; (3 ) 鞋 底模型内部区域的变形; (4 ) 鞋底模型外部区域适应性 变形 。其中, 在进行鞋底模型变形前, 鞋楦模型和鞋底 模型位姿已经匹配, 鞋楦模型和鞋底模型的宽度 、长度 和高度方向已经统一, 且与世界坐标 O-XYZ 方向已经对 齐, X 对应宽度方向, Y 对应长度方向, Z 对应高度方 向, 因此, 本文变形步骤中的水平维度为 XOY平面, 竖 直维度为 YOZ 平面, 鞋楦模型底面中轴线和鞋底模型内 部区域底面中轴线都在 YOZ 平面内。
3.1 基于径向基函数插值变形原理
径向基函数是一种以样本到数据中心之间的径向距 离为参数的标量函数 。基于径向基函数插值变形原理是 根据控制点之间的几何关系拟合曲面, 随后以变形点与 控制点的几何距离为驱动, 代入拟合曲面之中, 反求变 形点位移量[15. 16] 。其基本步骤如下:
( 1 ) 选择合适变形区域, 选取特征点作为控制点, 选取其余点作为变形点;
( 2 ) 根据模型变形的要求, 计算出控制点的位移量;
( 3 ) 选择合适的径向基函数作为计算函数;
( 4 ) 计算控制点之间的径向基函数值, 根据径向基函数值与控制点的位移量, 建立空间节点位移的径向基 函数插值模型, 并求解坐标分量权重系数;
( 5 ) 计算控制点与变形点之间的径向基函数值, 根据径向基函数值和上面求取的坐标分量权重系数反求变 形点的位移量;
( 6 ) 原变形点加上各自对应的位移量, 即可得到变形后的模型。
3.2 鞋底模型变形步骤
3.2. 1 级放处理
由于鞋楦模型源自用户脚部数据, 而鞋底模型源自 企业模型库, 两者尺寸大小往往存在一定的误差, 需要 根据鞋楦模型长度与宽度尺寸对鞋底的尺码进行校正, 进而减少后续变形操作的变形量, 提高精确度。
进行级放处理时尽量保持鞋底模型纹理形状等局部 特征和位姿关系不变, 因此, 将鞋楦模型底面中轴线和 鞋底模型内部中轴线投影在水平面, 将两条投影线的首 尾余量作为间隙余量, 根据间隙余量确定缩放中心和缩 放比例, 计算方法如下。
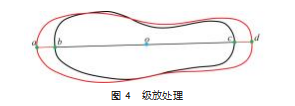
( 1 ) 在水平面上, 点 a 为鞋底中轴线头部端点 、点 b 为鞋楦中轴线头部端点 、点 c 为鞋楦中轴线尾部端点 、 点 d为鞋底中轴线尾部端点 。设点 o 为水平面上的缩放中 心点, 设 l1=a-o 、l2=d-o 、l3=b-o 、l4=c-o 、则满足条件: l1/l3=l2/l4. 从而计算出水平面上的缩放中心点 o 。如图 4 所示。
( 2 ) 将水平面上的缩放中心点 o 沿鞋底模型高度方 向 z投影回鞋底内部区域底面, 即可得到三维空间中的 缩放中心点p, 缩放比例为||l1 ||/||l3 ||。
3.2.2 鞋底模型水平维度的变形
该过程以鞋楦模型脚线作为驱动, 驱动鞋底模型内仁 线和模口线变形, 从而带动整个鞋底模型发生变形, 使鞋 底模型适应鞋楦脚线水平轮廓特征 。具体变形流程如下。
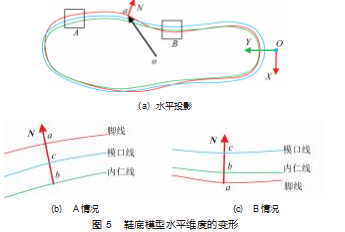
( 1 ) 将已提取的鞋楦模型脚线 、鞋底模型内仁线与 鞋底模型模口线投影到长度方向 Y 和宽度方向 X 所组成 的水平面上得到三者的水平投影线, 如图 5 所示。
( 2 ) 为提高后续径向基函数插值的稳定性, 对鞋楦 脚线的水平投影线上的点进行均匀采样, 经过采样筛选 后的顶点之间的欧氏距离大小相近, 分布更加均匀。
( 3 ) 设采样后鞋楦脚线的水平投影线上的点为 a, 利用 PCA算法可以计算点 a 的法线方向 N 并单位化, 但 是无法确定方向的正负, 因此设 o为鞋楦脚线点的数据 中心点, 设向量 l1=a-o, 若 N·l1 ≥0. 则 N 为正方向, 反 之则为反方向, 需要进行反向处理, 如图 5 中 N 为正方 向, 不需要反向处理。
( 4 ) 由点 a 计算出鞋底模型内仁线和模口线的控制 点和形变量 (形变量为向量), 具体为: 延长鞋楦脚线点 a 的法线方向 N, 分别交鞋底模型内仁线和模口线的水平 投影线于 b 和 c, 如图 5 中 A、B 两种情况, A 情况时鞋楦 与鞋底发生干涉, B 情况时鞋楦与鞋底存在间隙 。将 b 作 为鞋底模型内仁线的控制点, c 作为鞋底模型模口线的 控制点, 设向量 l2=b-a, 根据间隙距离值 t, 计算控制点 b的形变量 Vb= N×t- l2. 为保证鞋底模型内部侧壁特征不 变, 控制点 c的形变量保持和控制点 b 一样的形变量, 则 控制点 c 的形变量 Vc=Vb。
( 5 ) 重复计算出所有的控制点及其形变量, 将鞋底 模型的所有顶点作为变形点, 根据均化处理时设置的间 隔距离, 设置合适的径向基函数作用半径, 本文采用的 径向基函数为 Wendland’s C2 函数, 采用径向基函数插值 计算出变形点水平维度的位移量, 鞋底模型顶点加上各 自对应的位移量, 完成水平维度的鞋底模型变形。
3.2.3 鞋底模型外部区域竖直维度的变形
竖直维度的变形为鞋底模型外部区域的变形 。以鞋 楦底面中轴线点作为驱动, 驱动鞋底外部底面区域的中 轴线变形, 从而带动整个鞋底模型外部区域发生变形, 使鞋底模型外观适应鞋楦中轴线特征 。具体流程如下。
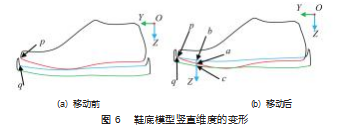
( 1 ) 用平面 YOZ 切割鞋楦和鞋底模型, 得到鞋楦和 鞋底在竖直方向上轮廓线, 如图 6 所示, 图中红色线段 为鞋楦模型底面中轴线, 蓝色线段为鞋底模型内部底面 中轴线, 绿色线段为鞋底模型外部底面轮廓线。
( 2 ) 由于鞋楦模型底面和鞋底模型内部底面在 Z 方 向间隙太大, 为避免下一步鞋底内部区域的变形中, 对 鞋底内部区域结构造成过大的破坏, 需要将鞋楦模型沿 Z方向移动 d 。设鞋楦底面中轴线头部端点为p 、鞋底内 部底面区域中轴线头部端点为 q 、 向量 l1=p-o、 向量 l2= p-o, 则移动距离 d=l1 ·Z- l2 ·Z, 若 d>0. 则沿 Z 方向移 动, 若 d<0. 则沿 Z 反向移动, 如图 6 (b) 所示。
( 3 ) 为提高后续径向基函数插值的稳定性, 对鞋楦 底面中轴线点进行均匀采样。
( 4 ) 设均匀采样后鞋楦底面中轴线上的点为 a, 过 点 a 做平行 Z 方向的直线与鞋底交于 b、c 两点, 将点 c 作 为控制点 。为保证鞋底厚度尽量不做改变, 即控制 b、c 两点之间距离不变, 设向量 l3=b-a, 向量 Vz为 Z 方向的 单位向量, 根据间隙距离 t, 计算出控制点 c 的形变量 Vc。
( 5 ) 重复计算出所有的控制点及其形变量; 将鞋底 模型外部区域的所有顶点作为变形点, 设置合适的径向 基函数作用半径, 采用径向基函数插值计算出变形点竖 直维度的位移量, 鞋底模型外部区域的顶点加上各自对 应的位移量, 完成竖直维度的鞋底模型外部区域变形 。 3.2.4 鞋底模型内部区域的变形完成鞋底模型外部区域变形后, 以鞋楦模型顶点为 驱动, 驱动鞋底模型内部区域发生变形, 使得鞋底模型 内部区域符合鞋楦模型的曲面特征约束, 具体流程如下。
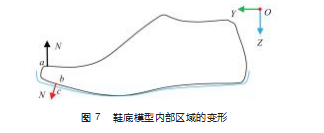
( 1 ) 计算鞋楦模型所有顶点的单位法矢 N, 筛选有效驱动顶点 。对于任一鞋楦顶点, 沿其顶点法矢方向 N 的射线与鞋底模型内部区域有交点, 则为有效驱动顶点, 如图7所示, 黑色线为鞋楦模型, 蓝色线为鞋底内部区域, 点 a 为无效驱动顶点, 点 b 为有效驱动顶点 。为提高求交计算效率, 对鞋底模型内部区域建立八叉树数据结构, 加速有效驱动顶点的筛选。
( 2 ) 为提高后续径向基函数插值稳定性, 对有效驱动顶点进行均匀采样。
( 3 ) 计算采样顶点 b沿其单位法矢方向 N 的射线与 鞋底模型内部区域的交点 c, 将 c 作为控制点, 设向量 l1= c-b, 根据间隙距离t, 计算控制点c 的形变量Vc=N×t- l1.
( 4 ) 重复计算出所有的控制点和形变量, 将鞋底模 型内部区域的所有顶点作为变形点, 设置合适的径向基 函数作用半径, 采用径向基函数插值计算出变形点的位 移量, 鞋底模型内部区域的顶点加上各自对应的位移量, 完成鞋底模型内部区域变形。
3.2.5 鞋底模型外部侧壁区域适应性变形
上一步中鞋底内部区域发生了变形, 因此鞋底外部 侧壁区域需要根据内部区域变形情况进行适应性变形 。该过程以鞋底模口线为驱动, 驱动鞋底外部区域侧壁部 分发生变形 。为保证鞋底侧壁高度不变, 只在水平维度 上进行适应性变形 。具体流程如下。
( 1 ) 为了提高后续径向基函数插值的稳定性, 对鞋 底模型模口线上的点进行均匀采样。
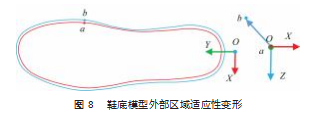
( 2 ) 设鞋底内部变形前的鞋底模型模口线上的顶点 为 a, 将 a 作为控制点, 设变形后的鞋底模型模口线上的顶点为 b, 设向量 l1=b-a, 向量 Vz为 Z 方向的单位向量, 同时, 因为只在水平维度上进行变形, 如图 8 所示, 则 控制点 a 的形变量 V=Vz× (l1 ·Vz)。
( 3 ) 重复计算出所有的控制点和形变量, 将鞋底模 型外部侧壁区域的顶点作为变形点, 设置合适的径向基 函数作用半径, 采用径向基函数插值计算出变形点水平维度的位移量, 鞋底模型外部区域的顶点加上各自对应 的位移量, 完成鞋底模型外部区域适应性变形。
完成所有变形步骤后, 无论是鞋底模型的内部区域 还是鞋底模型的外部区域都将适应鞋楦模型的特征。
4 实验验证
为验证本文算法的有效性, 在 Windows 平台 VC++ 2017 环 境 下, IntelⓇCore ( TM) i7-9700 3.00 GHz CPU, 16GB 内存 PC机上实现本文算法, 实验效果如下所示。
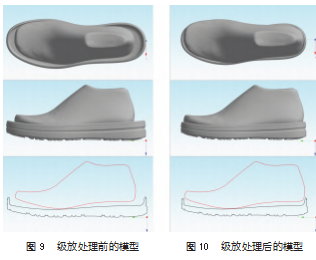
对比图 9 和图 10 可知, 级放处理后鞋楦模型与鞋底 模型尺码关系更加准确, 同时鞋楦模型与鞋底模型的位 姿关系依旧保持良好, 但图 10显示, 鞋底模型与鞋楦模 型有着较大的差距。
经测试, 均化处理时的间隔距离设置为 5 mm 时, 径 向基函数的作用半径设置为 100 ~ 150 mm, 变形效果和 稳定性较好 。对比图 11 和图 12. 在个性化变形后的鞋底 模型的外部区域特征更加适应鞋楦模型的形体特征, 鞋 底模型的整体形状外观更符合个性化定制的要求 。并且 该个性化变形效果良好, 鞋底模型不会出现拉伸 、撕裂 和扭曲等错误现象, 同时在符合变形要求的基础之上, 尽可能保持了鞋底模型的纹理特征。
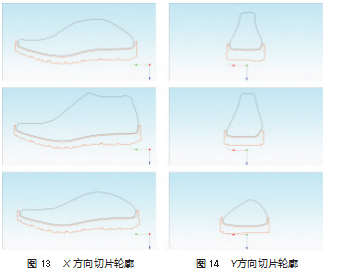
为验证鞋底模型内部区域能否适应鞋楦模型的特征, 对个性化变形后的鞋楦模型和鞋底模型进行切片, 如图 13和图 14.图 13 中依次为变形后鞋楦模型和鞋底模型在 x=-20 mm、x=0 mm、x=20 mm 三个截面上的切片轮廓;
图 14 中依次为变形后鞋楦模型和鞋底模型在 y=60 mm、y =120 mm、y=180 mm 三个截面上的切片轮廓 。图 13 ~ 14 显示个性化变形后的鞋楦模型和鞋底模型的切片轮廓在 两者接近处的法向间距较为均匀, 说明个性化变形后的 鞋底模型内部区域更加适应鞋楦模型的曲面特征, 达到 个性化定制的适应脚部特征的要求。
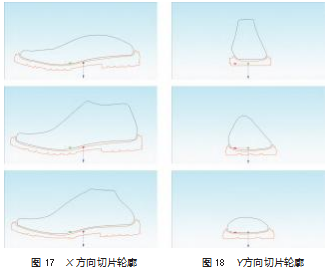
为进一步验证算法的健壮性, 在同样实验环境下做 了第二个鞋底模型的个性化定制变形实验, 实验效果如 图 15 ~ 18 所示 。对比图 15 与图 16. 显示变形后第二个 鞋底模型的形体特征也能够很好地匹配鞋楦模型的特征。
图 17 中 依 次 为 变 形 后 鞋 楦 模 型 与 鞋 底 模 型 在 x=-20 mm、x=0 mm、x=20 mm 三个截面上的切片轮廓; 图 18 依次为变形后鞋楦模型和鞋底模型在 y=-70 mm、 y=-20 mm、y=30 mm 三个截面上的切片轮廓 。图 17 ~ 18 显示个性化变形后的第二个鞋底模型的内部区域也更加 适应鞋楦模型的曲面特征。
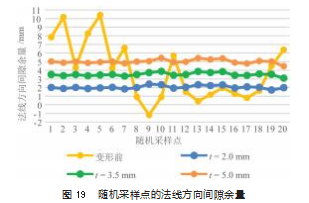
为进一步验证鞋楦模型与鞋底模型内部区域的法线 方向的间隙余量是否达到变形后的设计要求, 在图 12所 示鞋底模型变形后, 对鞋楦模型顶点进行随机采样, 计 算采样点沿其法线方向到鞋底模型内部区域的间隙余量, 将其作为评价变形效果的指标 。如图 19所示, 黄色线段 为变形前的间隙余量, 差异较大, 说明鞋底模型内部区 域不符合鞋楦模型曲面特征约束 。而蓝色 、绿色和橙色线段分别为预设的间隙距离值 t=2.0 mm、t=3.5 mm 和t= 5.0 mm 时变形后的实际间隙余量, 可以发现变形后的间 隙余量与预先设定的间隙距离值的差值误差在±1mm 之 内, 表明变形后的鞋底模型内部区域比较贴合鞋楦模型 的曲面特征, 且蓝色 、绿色和橙色线段的波动性不大, 反映变形也较为稳定, 因此本文鞋楦特征驱动的鞋底模 型个性化定制变形方法能够根据鞋楦模型的特征有效地 实现鞋底模型的个性化定制变形, 变形效果较为良好。
5 结束语
本文提出了一种基于径向基函数插值的鞋底模型变 形方法 。 由于径向基函数作用半径难以确定, 导致径向 基函数稳定性难以保证, 针对径向基函数这一特点以及 鞋底模型变形特点, 本文从变形策略的角度出发, 通过 采用合适的变形策略, 解决径向基函数插值方法在鞋底 模型变形中所暴露的问题 。本文为实现鞋楦模型特征数 据驱动的鞋底模型复杂变形, 在鞋底模型级放后将鞋底 模型变形过程分为 4个步骤, 即鞋底模型水平维度变形、 鞋底模型外部区域的竖直维度变形 、鞋底模型内部变形、 鞋底模型外部侧壁部分的变形; 每次变形中, 选择合适 的控制点及变形量后, 利用径向基函数插值方法进行变 形 。算法实例表明本文的变形策略能够有效实现较为精 确的鞋底变形控制, 使得鞋底模型适应个性化鞋楦特征。
目前针对鞋底模型个性化定制变形的研究较少, 但 是鞋底个性化定制对于人体健康和提高企业竞争力具有重 要意义。本文提出的鞋底模型个性化定制变形方法具有较 好的可行性和有效性, 但与实际的鞋底模型设计过程中采 用特征参数不一样, 因此穿着舒适性有待进一步验证。
参考文献:
[1] Buldt A K, Menz H B.Incorrectly fitted footwear, foot pain and foot disorders: a systematic search and narrative review of the lit ‐ erature[J].Journal of Foot and Ankle Research, 2018 (1):1-11.
[2] Thomas W Sederberg, Scott R Parry. Free-form deformation of solid geometric models[J].ACM SIGGRAPH Computer Graphics, 1986.20(4):151-160.
[3] 赵文彬,郑广平,张艳宁 . 直接点操作的人脸变形与动画[J]. 计 算机工程与应用, 2007. 43(23):3.
[4] Magnenatthalmann N, Laperrire R,Thalmann D, et al. Joint-de ‐ pendent local deformations for hand animation and object grasp ‐ ing[J].Graphics Interface,1989:26-33.
[5] Le B H,Hodgins J K.Real-time skeletal skinning with optimized centers of rotation[J]. ACM Transactions on Graphics, 2016. 35 (4):1-10.
[6] Zorin D.Interactive multiresolution mesh editing[C]// Conference on Computer Graphics & Interactive Techniques. ACM Press/Ad ‐ dison-Wesley Publishing Co. 1997.
[7] Dhibi N,Amar C B.Multiresolution analysis relying on Beta wave ‐ let transform and multi-mother wavelet network for a novel 3D mesh alignment and deformation technique[J].International Jour‐ nal of Machine Learning and Cybernetics, 2020. 11(12):1-15.
[8] William M Hsu,John F.Hughes,Henry Kaufman. Direct manipula ‐ tion of free-form deformations[J]. ACM SIGGRAPH Computer Graphics,1992.26(2):177-184.
[9] Alexa M.Differential coordinates for local mesh morphing and de ‐ formation[J].The Visual Computer,2003. 19(2):105-114.
[10] Yu Y ,K Zhou,Xu D,et al.Mesh Editing with Poisson-Based Gradient Field Manipulation[J].ACM Transactions on Graphics, 2004.23(3):644-651.
[11] Hardy R L.Multiquadric equations of topography and other ir ‐ regular surfaces[J]. Journal of Geophysical Resarch, 1971 (8): 1905-1915.
[12] 孙立镌,靳辉 . 一种新型神经网络在自由曲面重构中的应用 [J].计算机工程与应用, 2007. 43(32):3.
[13] Sheng C,CB Allen.Efficient Mesh Deformation Using Radial Ba ‐ sis Functions on Unstructured Meshes[J]. Aiaa Journal,2013.51 (3):707-720.
[14] Niu J,Lei J,He J.Radial basis function mesh deformation based on dynamic control points[J]. Aerospace Science and Technolo ‐ gy, 2017. 64(5):122-132.
[15] 刘中玉,张明锋,聂雪媛,等 .一种基于径向基函数的两步法网 格变形策略[J]. 力学学报,2015.47(3):534-538.
[16] 王军涛,孙劲光,杨新年 .基于误差驱动与 CSRBF 的点云重建 [J].计算机工程与应用,2011.47(31):151-153.
关注SCI论文创作发表,寻求SCI论文修改润色、SCI论文代发表等服务支撑,请锁定SCI论文网!
文章出自SCI论文网转载请注明出处:https://www.lunwensci.com/ligonglunwen/59078.html