SCI论文(www.lunwensci.com)
摘要:采用一种自制线型自由液面静电纺丝装置考察聚合物溶液浓度 、工作电压 、喷头转速及电极丝直径 4 个工艺参数对聚合物 泰勒锥成形及其线密度的影响, 应用响应面法设计实验方案, 同时建立工艺参数与聚合物泰勒锥尺寸间的数学模型, 量化响应与 输入间的关系 。实验中泰勒锥平均尺寸为 0.327~0.797 mm, 相对标准偏差为 8. 19%~14.31%, 平均线密度为 0.583~0.237 pcs/mm 。研 究结果表明: 一定条件下 PVDF 泰勒锥平均直径随着聚合物溶液浓度 、工作电压的增加而减小, 随着电极丝直径的增加而增大, 受喷头转速影响较小; 并得出上述 4 个因素对泰勒锥平均直径的影响由大到小依次排序为: 电极丝直径 、溶液浓度 、工作电压、 喷头转速。
关键词 :静电纺丝,PVDF, 泰勒锥成形, 响应面法
Influence Analysis of Self-organization Forming of Taylor Cone in Linear Electrospinning
Xing Sheng, Zhou Haiying ※, Huang Junjie
(School of Mechanical and Electronic Engineering, East China Institute of Technology, Nanchang 330013. China)
Abstract: A self-made linear free liquid surface electrospinning device was used to investigate the effects of four process parameters : polymer solution concentration, operating voltage, nozzle speed and electrode wire diameter on the forming of polymer Taylor cones and their linear density. The experimental scheme was designed by the response surface methodology, and the mathematical model between the process parameters and the size of the polymer Taylor cone was established, and the relationship between the response and the input was quantified. In the experiment, the average diameter of Taylor cone was 0.327~0.797 mm, the relative standard deviation was 8. 19%~14.3%, and the average linear density was 0.583~0.237 pcs/mm. The research results show that under certain conditions, the average diameter of PVDF Taylor cone decreases with the increase of polymer solution concentration and operating voltage, and increases with the increase of electrode wire diameter, which is less affected by the rotation speed of the nozzle. And it is concluded that the influence of the above four factors on the average diameter of the Taylor cone is ranked in descending order: electrode wire diameter, solution concentration, operating voltage, and nozzle speed. Key words: electrospinning; PVDF; Taylor cone forming; response surface methodology
引言
聚合物纳米纤维在军工 、环境 、医疗和新能源等领 域的应用研究取得了显著进展, 其高质量 、低成本宏量 制备方法研究引起很多学者的关注[1] 。线型静电纺丝具 有结构简单 、工作稳定 、易拓展等特点, 具有很好的应 用前景[2] 。泰勒锥形态和密度是影响纳米纤维质量和产 量的关键因素, 对其开展研究有助于调控线型静电纺丝 过程 。文献表明, 由于 Plateau-Rayleigh 不稳定性特性, 小型圆柱元件表面的液体射流和液体薄膜是不稳定的, 在液体表面张力作用下会分解成一系列的小液滴[3] 。这 种现象在纤维制造 、金属丝涂层 、静电纺丝 、燃料电池、 光纤 、外科纺织品和雾/液滴过滤等领域得到了广泛的 应用[4] 。当圆柱形元件上附着液膜时, 通常会观察到液膜自发破裂形成液珠, 并以规则的间隔附着在元件上, 甚至当液体与固体元件间的接触角明显为零时, 这种液 膜破裂形成液珠的现象也可能发生[3] 。过去几十年里, 众多国内外科研工作者深入展开了多方面的研究[5-6]。 Plateau[7]和 Rayleigh[8-9]提出圆柱形元件外表面上形成的涂 层薄膜存在一定正曲率和负曲率区域, 正 、负曲率区域 存在一定压力差, 从而产生了由于压力梯度导致的流体 流动[10] 。这种内部通量导致位移振幅的增长, 最终形成 泰勒锥 。Goren[11]讨论了金属丝上和小管内的环形液体涂 层在自由表面毛细力作用下的不稳定性, 并证明了 Oh ‐ nesorge 数在各扰动中起关键作用 。Yarin[12]提出了受电场 影响的液滴稳定形状的理论, 当液体表面达到喷丝前的 临界状态时, 其形状接近于半角为 33.5°的圆锥体。
本文主要是基于自主改进并搭建的线型自由液面静 电纺丝实验装置, 考察了聚合物溶液浓度 、工作电压、 旋转速度和电极丝直径这 4 个主要工艺参数对聚合物泰 勒锥成形及其线密度的影响, 并分析了单个工艺参数对 聚合物泰勒锥成形的影响 。研究结果可为后续的实验装 置改进与实验设计优化提供一定的思路, 为线型自由液 面静电纺丝装置的深入研究提供参考。
1 实验部分
1.1 试剂与仪器
聚偏二氟乙烯 (Poly Vinylidene Fluoride, 以下简称 PVDF ), P302009- 100g 型, 上海阿拉丁生化科技股份有 限公司; N-N-二甲基甲酰胺 ( N, N-dimethylformamide, 以下简称 DMF), 纯度大于 99.5%, 上海阿拉丁生化科技 股份有限公司; 去离子水, W119424-25L 型; 数显恒温 磁力搅拌器: 型号 85-2B, 山东欧莱博仪器有限公司; 高 压 电 源: 型 号 DW-P104-5ACB2. 最 高 输 出 电 压 为 100 kV, 东文高压电源 (天津) 股份有限公司; 电子天 平: MTB 2000. 深圳市美孚电子有限责任公司; 拍摄相 机传感器: 索尼 IMX707. 分辨率 3 840×2 160. 最大帧 率 60 帧/s, 传感器尺寸 1/1.28 inch, f/1.9 光圈。
1.2 实验过程
PVDF/DMF 溶液配置: 称取一定质量的 PVDF 药品 和溶剂 DMF 按照一定的比例混合, 样品放置于恒温磁力 搅拌器中搅拌, 设置恒温 60 ℃, 加热搅拌时长约为 3 h, 得到澄清透明溶液, 放置于室温下, 静置去除气泡后备用。 1.3 测试与表征采用相机测定待测溶液实验过程中泰勒锥成形情况, 恒定帧率 60 帧/s, 分辨率 3 840×2 160. 每组实验 拍摄 3 min。
1.4 线型自由液面静电纺丝装置及电纺过程
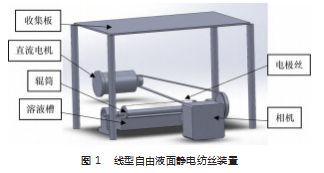
图 1 所示为自制线型自由液面静电纺丝装置示意图, 主要包括电极丝 、溶液槽 、收集板 、齿轮传动装置 、电 机 、辊筒 、相机等 。实验过程中, 3 根呈 120°分布的铜 丝安装在金属轴上, 金属轴连接上带轮, 带轮与一个由 直流电机驱动的皮带相连, 使用调速器控制电机, 以实 现辊筒的转速控制。
实验过程中, 高压电源正极连接收集板, 负极连接 电极丝和辊筒 。当电极丝通过聚合物溶液浴时, 溶液挟 带在电极丝上, 形成一层溶液薄膜覆盖在导线上 。 由于 瑞利-泰勒不稳定性, 溶液薄膜在电极丝上分解成单个 的带电聚合物液滴 。图 2 所示为实验过程中液滴成形图; 图 3 所示为实验过程中泰勒锥成形图。
1.5 响应面法与实验设计
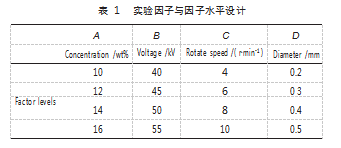
本实验设计基于响应面法 ( RSM ) 可以量化测量到 的响应与多个重要输入因子之间的关系[13] 。采用基于单 因素法的响应面法进行实验设计 。结果表明, 泰勒锥自 组织成形的影响因素包括以下几种: 聚合物溶液浓度 (wt%)、 工作电压 (kV)、 旋转速度 (r/min) 和电极丝 直径 (mm), 并考察了这 4 个参数对泰勒锥成形直径的 影响 。各因子及因子水平如表 1 所示 。基于 CCD, 响应 值 (平均泰勒锥直径) 与这 4 个因子 (A 、B 、C 和 D) 之 间 的 数 学 关 系 可 以 用 如 下 的 二 次 多 项 式 模 型 近
似[14- 15]:f (A, B, C, D) = α 0 + α 1 A + α 2 B + α 3 C + α 4 D + α 5 AB + α 6 AC + α 7 AD + α 8 BC + α 9 BD + α 10CD
式中: f为响应值; α n 和 βn ( n=1. 2. 3. 4. 5 ) 均为未 知系数, 通过实验数据确定。
每组实验过程拍摄 3 min, 所有实验均在常温(25± 1 )℃, 相对湿度(42±3)%下进行。
2 结果与讨论
2.1 实验结果
采用相机测定了 PVDF 泰勒锥成形形貌, 用图像处 理软件 ImageJ 测量泰勒锥直径, 测量每张照片上携带的 全部泰勒锥直径, 并统计其直径的平均值 ( MFD )、 泰勒 锥线密度 ( LD ) 和相对标准差 ( RSD ), 实验结果如表 2 所示。
2.2 测试与表征
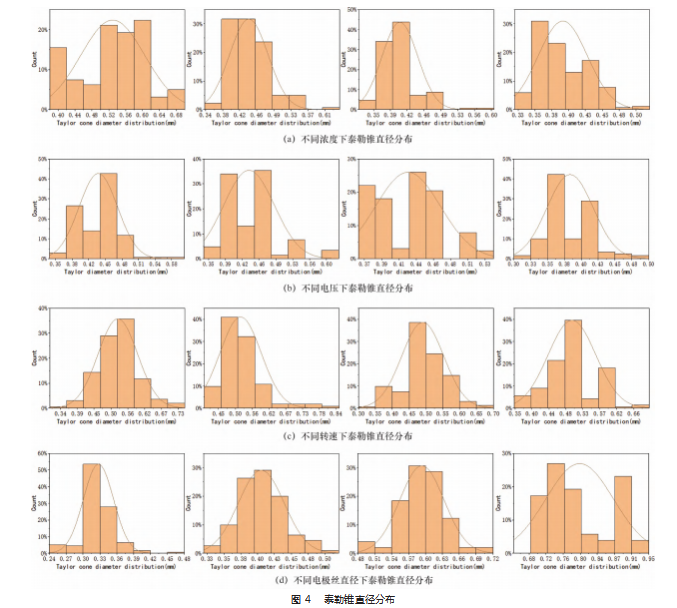
通过 ImageJ 测量出的数据分别按顺序绘制成的泰勒锥直径分布如图 4 所示 。实验设计中 PVDF 泰勒锥 MFD 范围为 0.327~0.797 mm。
在考察聚合物溶液浓度对泰勒锥成形影响的实验中, 浓度为 10% 的实验条件下, MFD 值最大, 图 5 (a) 为该条件下实验过程拍摄图; 浓度为 16% 的实验条件下, MFD 值最小, 图 5 (b) 为该条件下实验过程拍摄图; 浓 度为 16% 的实验条件下, LD 值最大, 图 5 (c) 为该条件 下实验过程拍摄图; 浓度为 14% 的实验条件下, LD 值最小, 图 5 (d) 为该条件下实验过程拍摄图 。于室温下, PVDF 溶液表面张力系数随着溶度的增大而降低, 分析 其原因在于图 5(b)中溶液浓度较大, 溶液表面层分子同 时受到本相内分子和另一相分子作用[16] 。 由于两相分子 性质不同, 溶液表面层分子受力的球对称性被破坏, 导 致溶液的表面张力降低, 因此观察到较为细小的泰勒锥, 同时线密度也最大。
在考察工作电压对泰勒锥成形影响的实验中, 工作 电压为 40 kV 的实验条件下, MFD 值最大, 图 6 (a) 为 该条件下实验过程拍摄图; 工作电压为 55 kV 的实验条 件下, MFD 值最小, 图 6 (b) 为该条件下实验过程拍 摄图; 工作电压为 55 kV 的实验条件下, LD 值最大, 图 6 (c) 为该条件下实验过程拍摄图; 工作电压为 40 kV 的实验条件下, LD 值最小, 图 6 (d) 为该条件下实验过 程拍摄图 。在较低浓度时, PVDF 溶液的粘度随着电场 强度的升高有一定程度的上升[17], 分析其原因在于图 6 (b) 中的电压较大, 其分子链运动的自由体积较大, 在较大电场力的作用下, 溶液表面电荷吸附力和活度增 加, 从而使泰勒锥表面张力减小, 泰勒锥在成形过程中 所需的克服表面张力的曲张扰动也较低, 因此观察到较 为细小的泰勒锥, 同时线密度也最大。
在考察旋转速度对泰勒锥成形影响的实验中, 转速 为 4 r/min 的实验条件下, MFD 值最大, 图 7 (a) 为该条 件下实验过程拍摄图; 转速为 8 r/min 的实验条件下, MFD 值最小, 图 7 (b) 为该条件下实验过程拍摄图; 转 速为 4 r/min 的实验条件下, LD 值最大, 图 7 (c) 为该 条件下实验过程拍摄图; 转速为 6 r/min 的实验条件下, LD 值最小, 图 7 (d) 为该条件下实验过程拍摄图 。旋转 速度所得实验数据中, 最大差值为 6.83%, 分析其原因在整个自由液面静电纺丝过程中电场力是主要驱动力, 电场力方向由电极丝指向收集板, 而由于辊筒旋转运动 产生的离心力相较于由静电场产生的电场力较低, 因而 泰勒锥成形影响较小。
在考察电极丝直径对泰勒锥成形影响的实验中, 电 极丝直径为 0.5 mm 的实验条件下, MFD 值最大, 图 8 (a) 为该条件下实验过程拍摄图; 电极丝直径为 0.2 mm 的实 验条件下, MFD 值最小, 图 8 (b) 为该条件下实验过程 拍摄图; 电极丝直径为 0.2 mm 的实验条件下, LD 值最 大, 图 8 (c) 为该条件下实验过程拍摄图; 电极丝直径 为 0.5 mm 的实验条件下, LD 值最小, 图 8 (d) 为该条件 下实验过程拍摄图。分析其原因在于电极丝直径变化不影 响金属自身的表面自由能; 而金属丝直径越大, 电极丝经 过溶液槽时挟带的溶液量越大, 导致电极丝表面形成的液 膜横截面积越大, 泰勒锥在成形过程中所需的克服表面张 力的曲张扰动也就越大, 泰勒锥形成时的接触角也就越 小, 因此形成的泰勒锥直径越大, 同时线密度也越小。
2.3 响应结果分析
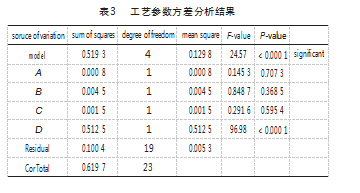
利用 Design-Expert 软件对单因素实验数据进行方差 分析得到结果如表 3 所示, 建立 PVDF 泰勒锥的MFD (f) 和 聚 合 物 溶 液 浓 度 (A )、 工 作 电 压 ( B )、 旋 转 速 度 ( C )、 电极丝直径 ( D ) 的多元二次回归方程模型:
f (A, B, C, D) = 0.504 5 − 0.008 A − 0.019 3 B +0.011 3 C + 0.206 7 D + 0.036 3AB + 0.031 7 AC − 0.037 5AD + 0.003 7 BC + 0.002 5 BD
为了研究模型的统计显著性, 提出了概率值 ( P 值), 它表示因素的显著性 。 当 P<0.05 时, 该因素对反 应有显著影响 。而当 P>0.05 时, 该因素对反应没有显著 影响 。R2 是另一个重要的因素, 用于研究模型的统计显 著性, 它决定了模型对观察到的反应的适应程度。
由表 3 可知, 模型 P<0.05 说明电极丝直径对聚合物 泰勒锥 MFD 的影响较大, p<0.000 1. 说明此模型的差异 较为显著, 方程较为合理 。对于 MFD 来说, 4 个影响因 素: 聚合物溶液浓度 (A )、 工作电压 ( B )、 旋转速度 ( C )、 电极丝直径 ( D ) 中, 电极丝直径对聚合物泰勒锥 MFD 影响最大, 随后是聚合物溶液浓度的影响, 而旋转 速度对聚合物泰勒锥 MFD 的影响程度较低 。综上, 4 个 因素对 MFD 影响大小顺序为电极丝直径 ( D ) >聚合物溶 液浓度 (A ) >工作电压 ( B ) >旋转速度 ( C )。
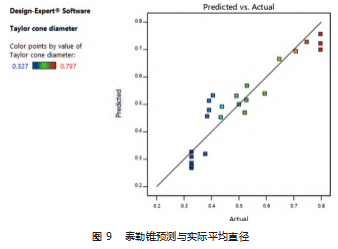
泰勒锥预测与实际平均直径如图 9 所示。
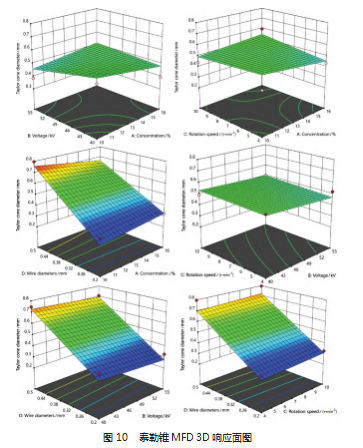
图 10 为泰勒锥 MFD 3D 响应面图, 由图可以看出, 泰勒锥 MFD 受电极丝直径影响最大, 呈同步增大趋势; 聚合物溶液浓度和工作电压影响较小, 泰勒锥 MFD 与之 呈反比关系; 旋转速度对泰勒锥 MFD 影响较小。
2.4 液滴成型模拟
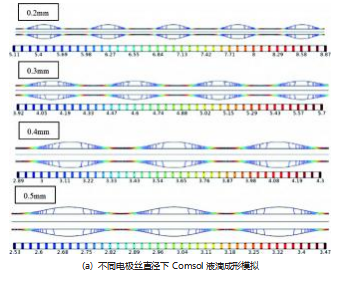
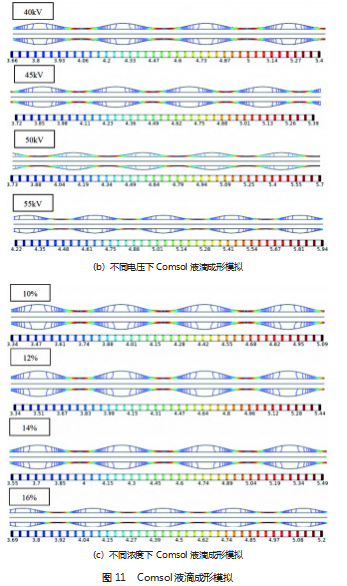
为了说明实验现象, 探究线型自由液面静电纺丝过 程中聚合物溶液泰勒锥自组织成形 。利用 Comsolmulti ‐ physics 模拟了不同聚合物溶液浓度 、工作电压和电极丝 直径条件下液滴的成形情况, 通过分析液滴成形过程中 压力分布, 进而推断泰勒锥自组织成形 。 图 11 (a) 为 不同电极丝直径下的液滴二维压力等值线图, 图 11 (b) 为不同聚合物溶液浓度下的液滴二维压力等值线图, 图 11 (c) 为不同工作电压下的液滴二维压力等值线图 。压力等值线图显示压力大小趋势从液膜正曲率区域到液膜 负曲率区域为由大到小 。结果显示, 电极丝直径对聚合 物液滴直径有较大影响, 聚合物溶液浓度和工作电压对 聚合物液滴直径影响较小 。流体压力随电极丝直径的增 大而减小, 导致液滴直径随增大, 但液滴线密度明显降 低; 流体压力随着工作电压的增大有少许增长, 导致液 滴直径降低, 液滴线密度有少量增加; 流体压力在溶液 浓度为 14% 时达到最大, 因而此时液滴线密度最小, 而 溶液浓度为 16% 时, 液滴直径最小 。流体模拟结果与相机观察到的实验结果相一致 。分析其原因在于电极丝表 面粗糙度引起的拉普拉斯压力差驱动液体向低压力的区 域集中, 最终出现液膜破裂, 聚并形成液滴。
3 结束语
本文采用一种自由液面的静电纺丝装置来替代传统 电纺中的毛细管喷丝 。设计实验并考察了 4 个主要工艺 参数对聚合物泰勒锥成形的影响, 结果表明:
( 1 ) 一定条件下, 聚合物泰勒锥 MFD 随着聚合物溶 液浓度 、工作电压的增加而减小, 随着电极丝直径的增 加而增大, 受喷头转速影响较小;
( 2 ) 通过响应面法建立了工艺参数与聚合物泰勒锥 尺寸间的多元二次回归方程模型, 量化了响应与输入间 的关系;
( 3 ) 利用 Comsolmultiphysics 模拟了不同条件下液滴 的成形情况, 模拟结果与实验结果相符。
然而, 目前线型自由液面静电纺丝过程中还有很多 现象和机理亟待研究 。因此, 还需要进一步探究纺丝过 程中各实验参数对实验的影响。
参考文献:
[1] 岳青,王绍德,徐飞,等 . 静电纺丝技术及其在各领域中的应用 [J]. 材料导报,2021.35(S1):594-599.
[2] 陈金平,胡良强,刘东运,等 . 纳米复合相变材料的制备和应用 研究综述[J]. 粉煤灰综合利用,2016(3):58-60.
[3] Roe R J. Wetting of fine wires and fibers by a liquid film[J]. Jour‐ nal of Colloid and Interface Science, 1975. 50(1): 70-79.
[4] Shabahang S, Kaufman J J, Deng D S, et al. Observation of the Plateau-Rayleigh capillary instability in multi-material optical fibers[J]. Applied Physics Letters, 2011. 99(16): 161909.
[5] 刘宇健,谭晶, 陈明军,等 . 静电纺纳米纤维纱线研究进展[J]. 纺 织学报, 2020. 41(2): 165- 171.
[6] 谭耀红,刘呈坤,毛雪 . 静电纺制备定向纳米纤维集合体的研 究现状[J]. 高分子材料科学与工程, 2018. 34(11): 183- 190.
[7] Plateau J A F. Statiqueexpérimentale et théorique des liquidessou ‐ mis aux seules forces moléculaires[M]. Gauthier-Villars, 1873.
[8] Rayleigh J W S B. The theory of sound[M]. Macmillan & Compa ‐ ny, 1896.
[9] Rayleigh J W S B. Scientific papers[M]. University Press, 1899.
[10] Breslouer O. Rayleigh-plateau instability: falling jet[J]. Project Report, 2010.
[11] Goren S L. The instability of an annular thread of fluid[J]. Jour‐ nal of Fluid Mechanics, 1962. 12(2): 309-319.
[12] Yarin A L, Koombhongse S, Reneker D H. Taylor cone and jet‐ ting from liquid droplets in electrospinning of nanofibers[J]. Journal of applied physics, 2001. 90(9): 4836-4846.
[13] Ahmadipourroudposht M, Fallahiarezoudar E, Yus of NM, Idris A. Application of response surface methodology in optimization of electrospinning process to fabricate (ferrofluid/polyvinyl alco‐ hol) magnetic nanofibers[J]. Mater Sci Eng C,2015(50):234-241.
[14] Sukigara S, Gandhi M, Ayutsede J. Regeneration of Bombyx mo ‐ ri silk by electrospinning: Part 2. Process optimization and em ‐ pirical modeling using response surface methodology[J]. Poly ‐ mer 2004(45):3701-3708.
[15] Gu SY, Ren J. Process optimization and empirical modeling for electrospun poly (d, l-lactide) fibers using response surface methodology[J]. Macromol Mater Eng, 2005(290):1097- 1105.
[16] 许巧平 . 有机化合物溶液表面张力系数与浓度关系的实验 研究[J]. 当代化工,2015.44(7):1461- 1464.
[17] 冯旭霞 . 高压电场下高分子溶液基本性能研究[D]. 广州:华 南理工大学,2015.
关注SCI论文创作发表,寻求SCI论文修改润色、SCI论文代发表等服务支撑,请锁定SCI论文网!
文章出自SCI论文网转载请注明出处:https://www.lunwensci.com/ligonglunwen/59008.html