面向STL格式零件规则特征表面点元素拾取及其法向矢量估算方法论文

　　分析STL格式文件的结构可知，该文件类型应用于接触式检测至少存在两个问题，分别分析如下。

　　（1）规则特征表面无点可拾取

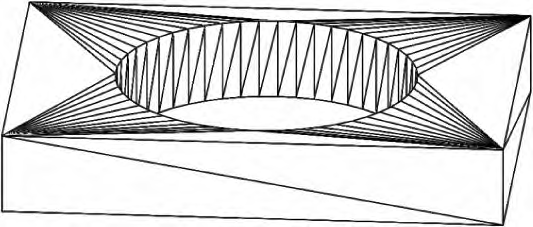
　　开发的数控加工精度在机检测系统能快速读取加工零件数字模型的STL格式文件并进行三维渲染，可通过电脑屏幕操作鼠标任意拾取零件模型上的点元素作为在机检测的基准（即设计理想点），为下一步的检测路径生成和检测结果对比提供理论依据。然而由于STL格式模型表面特征全部由三角面片（只由3个顶点的坐标+1个表示面片方向的法向矢量组成）近似勾勒而成，只有三角面片上的3个顶点才是三维数字模型表面上的原始几何元素。所以对于零件上的平面、键槽、圆柱或孔等规则特征的表面并非曲面，而是只有三角面片（只在特征边缘处有顶点），如图1所示为一带孔长方体的STL格式模型，要直接拾取该数字模型内的表面（包括孔壁和平面）的测量点是无法实现的。

　　（2）测点法向矢量的精确计算问题

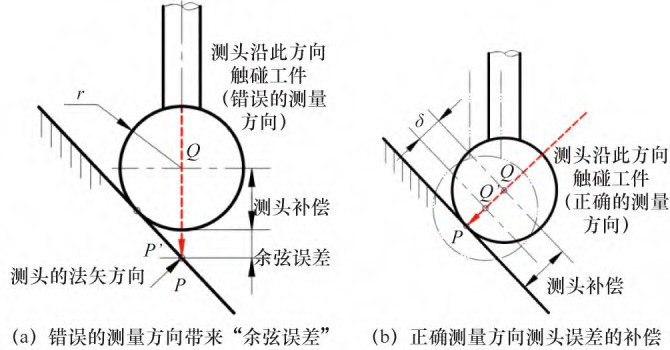
　　接触式检测的测头是一个有一定直径的圆球，当测球触碰工件表面时，机床所记录的当前点的位置实质上是经补偿探针长度后得到的测球的中心，因此还需要沿着测量方向再补偿测球的半径r才能真正得到触碰点的位置，所以如果测量方向（通常选择工件表面触碰点的法矢方向）不正确，必将引起较大的测量误差[3]。如图2（a）所示，测头从工件的正上方往下（-Z方向）运动拟触碰工件上的P点，由于测球有一定的直径，在测头下探的过程中测球边缘先触碰到P′点即停止了-Z方向运动并立即将当前球心（Q点）位置锁存，此时再沿-Z方向补偿测球半径r得到的位置与拟测点P点还差一“余弦误差”[4]。实践已证实，接触式检测时测头沿着测点所在表面的法矢方向触碰工件是获得精确测量位置的必要条件。而STL格式的数字模型因表面元素严重缺失致使测量点法矢的精确计算存在较大问题。

　　2平面特征点元素获取及其法矢估算

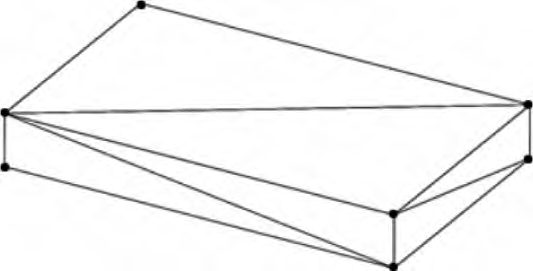
　　STL格式零件模型上的平面特征全部由连接边缘处的三角面片组成，如图3所示，所有可拾取到的点元素（即三角面片的顶点）均位于零件的边缘转角处，无法直接用于接触式检测。因此，基于零件STL格式模型的在机接触式测量系统要顺利实现平面特征的测量，必须要先获取得到平面上的点作为测量点。

　　2.1平面特征的拾取

　　课题组开发的在机检测软件读入零件模型并在主界面渲染出零件的原貌，对于操作用户而言，“所见即可选，所选即可得”是基本的要求。OpenGL基于名字堆栈和命中记录的拾取机制可解决此类问题，该拾取机制是利用鼠标的位置调用了一个叫gluPickMatrix()的矩形拾取库函数，鼠标单击时即在鼠标单击位置定义了一个由屏幕往里的狭长形的视景体，所有进入此选择视景体的元素都会被选中。检测元素的拾取是要求所看见的最外层（即靠近屏幕层）被选中，因此选择时要做到“有的放矢”。课题组基于OpenGL拾取技术，巧妙地利用指向对象指针值的唯一性对其选择模式进行了优化处理，只将落在鼠标点选位置确定的视景体之内的第一个（最上层）三角面片的名称存储在一个堆栈中，即可确定拾取到所要的三角面片。为提高拾取效率，系统设计了“矩形快速拾取”和“鼠标点选拾取”两种三角面片的模式。

　　2.2平面测量点的获取

　　鉴于STL格式零件模型上的所有平面均由简化的三角面片组成，其顶点全部位于平面的边缘位置，是无法直接应用于接触式检测的。一种简单的处理方法就是通过计算平面上每个三角形的重心位置的坐标值作为三角面片上的测量点，选用此方法需要拾取待检测平面上的至少3个三角面片（每个三角面片生成1个测点，3点即可表示1个平面）。

　　在直角坐标系中，任一空间三角形重心的坐标应是其3个顶点坐标的算术平均数（如图4所示），即空间三角形重心的坐标为：

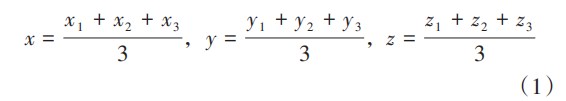
　　检测开始实施前，通过鼠标点选待测平面所有的三角面片并返回每个三角面片3个顶点坐标值并代入式（1）计算各个三角面片的重心坐标，增加“生成单个平面测点”菜单功能，调用计算所有已选择三角形的重心坐标保存作为测量的理想点元素，并实时推送至界面显示出来。

　　而对于图3所示的规则平面，当表达某一平面的三角面片数少于3时，则生成的测点数无法满足平面测量的最少元素要求，因此还需考虑只有两个三角面片或只在某一个三角面片上检测至少3个点的情况。通常地，检测零件的某区域所选点是随机拾取的，因此三角面片上的测点可借助随机函数rand()来生成。在三角形里随机生成点是与三角形的顶点位置有关的，因此顶点间的向量也是决定生成点位置的关键因素。假定三角形顶点A、B和C，那么可得两个向量：

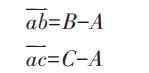
　　由随机函数rand()生成2个0~1的随机数x和y并确保x+y的值不大于1，那么可得随机点：

　　2.3平面测点法矢获取

　　由前面对STL格式文件结构的分析可知，任意一个三角面片都有现成的法向矢量，因此可以直接选取该平面内任一个三角面片并调用其法向矢量值作为接触式检测的方向。

　　3圆柱特征点元素获取及其法矢估算

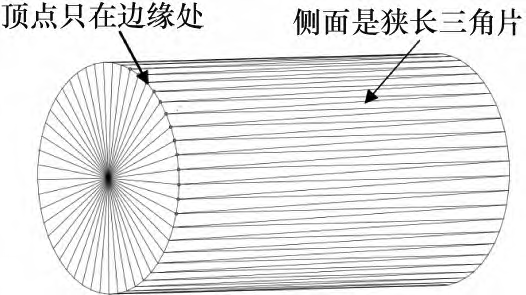
　　STL格式下三维模型的圆柱孔（或轴）壁被简化为狭长的三角面片，只有圆柱孔（或轴）两端的边缘处才有原CAD模型上的“点特征”，三维软件导出的STL格式的圆柱数字模型如图5所示，由于此类规则特征侧壁上根本没有点特征，实施在机检测时孔壁上的测量点是无法通过鼠标直接在屏幕上点选得到的。因此，快速、准确地获取规则特征表面上点元素是实现面向STL格式零件规则特征在机检测顺利实施的先决条件。

　　3.1圆柱壁测量点的获取

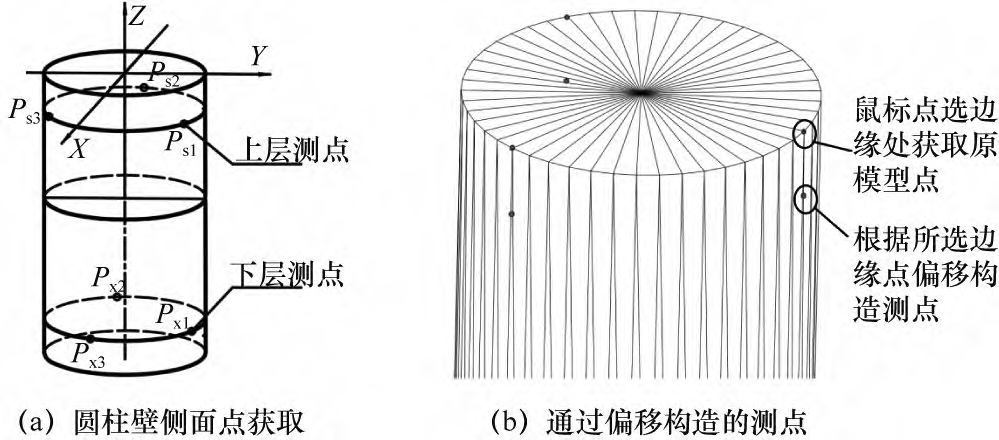
　　对于圆柱（轴和孔可类似看待）类规则特征，结合STL格式文件的特点，只能从两端边缘处的原CAD数模的点元素着手考虑重构内壁位置点以满足检测的需要。在机检测实施前需要用户拾取（或重构）待检测位置的点元素特征，然后根据系统算法优化检测路径。为了更好地反映被测圆柱的特征，圆柱表面的检测需要分布在圆柱壁的2层且至少5个点。

　　STL格式模型上的孔或轴类特征边缘处的点元素就是CAD数模表面上的点，但是这些边缘位置无法直接用于接触式检测，即拾取到的边缘点是不能作为检测原始理想点的。由于普通三轴数控机床只能加工与坐标轴平行的孔，因此对于孔特征而言，可通过鼠标拾取孔边缘处的多个点特征（拾取的2个点元素之间的跨度要尽可能地大，每个圆面建议共拾取应不少于3个点），然后沿孔深度方向（对于在机检测，通常是+Z或=Z向）偏移一定的距离（一般至少要达到测球直径的2倍，也可根据孔深或轴长在弹出的设置对话框里自行选择确定）。如果要检测圆柱度误差等空间特征，还需在孔的另一头的边缘处拾取同样数量的孔元素并完成类似的偏移，此时要充分考虑现有探针的长度，必要时可安装加长探针以确保检测结果能充分还原加工孔的原貌，如图6（a）所示，根据边缘所选点偏移生成的测点如图6（b）所示。

　　3.2圆柱壁测点法矢估算

　　根据课题组前期的实验验证，测球半径所带来的误差是接触式测量主要的误差来源[5]。因此，为了提高测量结果的精确度，应规范测头触碰工件的方法，前期大量的实验已验证，只有沿着测点法向矢量触碰工件才能有效地避免因测球半径所带来的余弦误差。因此，计算出相对精确的圆柱壁测点的法向矢量是实现圆柱壁精准测量的首要前提。经多次试验，得到以下两种估算圆柱孔壁任意点法矢的方法。

　　（1）规则圆柱孔壁任意点法矢

　　对于规则型孔，垂直于孔轴线的任意一平面内（比如某一边缘）的3个点可形成一个圆，任意点指向该圆圆心的方向即为该点的法向矢量。

　　（2）非规则圆柱孔壁任意点法矢

　　计算三角网格任意顶点法矢最常用的方法是最早由Taubin[6]提出的离散估算法，其计算公式为：

　　式中：Aj为点集N(v)中以任意点vi为顶点的第j个三角面片的面积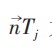；为以任意点vi为顶点的单位法矢。

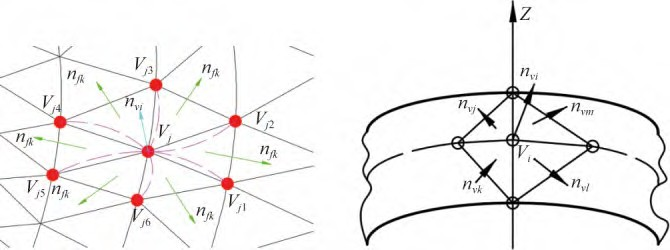
　　由前述可见圆柱孔壁的三角面片都是一些狭长形的三角形，尤其在曲面突变严重区域其法矢方向与平缓区域是截然不同的，而式（3）并没有考虑三角面片形状的影响，因此神会存[7]在Taubin提出的方法的基础上考虑了三角面片形状所带来的影响，即增加了三角形角度的权重，式（3）被修正为：

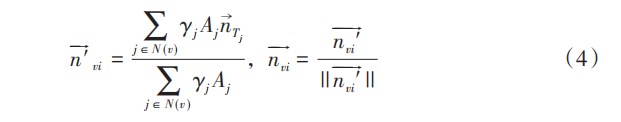
　　其中γj表示点集N(v)中任一点元素vi为顶点并与其相邻的第j个三角面片在vi处的内角大小，依次将各个相邻三角面片的角度权重加起来后进行单位矢量化，即得到了三角面片任意顶点vi处的法矢：

　　式中：

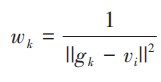
　　为充分考虑三角面片形状的质心权重；

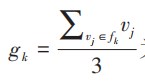
　　为第k个三角面片fk的质心。

　　改良后的式（5）充分考虑了任意一点vi的法矢受邻近各三角面片的走向所影响，如图7（a）所示，经验证其所估算的三角网格曲面任意顶点位置法矢的精度完全可满足接触式检测工件的精度需要，对于非规则圆柱孔壁任意点法矢均可利用式（5）进行估算。但是类似椭圆形孔等特征仍然只有孔两端的边缘处才有顶点，孔内壁的表面只有狭长的三角面片，因此需要特别处理一下。课题组根据式（5）计算顶点法矢对邻接三角面片元素的需要，通过已选点人工拟合圆的方法在任一测点周边构造出邻近至少4个顶点，如图7（b）所示，估算的法矢值与CREO计算得到的法矢值偏差在5%以内，如果排除计算机不同进制间数据转换和位数截取所带来的误差，该偏差基本可忽略，因此，通过该方法得到的测点法向矢量完全可以满足在机检测对测点法矢的精度要求。

　　4结束语

　　基于数控加工精度在机检测系统实施在机检测时零件STL格式数模下其规则特征测点无法拾取及其法向矢量无法精确计划等问题，提出了规则平面、规则孔和非规则孔孔壁测量点的生成策略，并在构造的邻近测点的基础上对孔壁任意测点的法向矢量进行了估算，与三维软件所计算的法向矢量进行对比表明误差完全可满足在机检测的精度要求，实现了零件STL格式数模规则孔特征表面的在机检测。

　　参考文献：

　　[1]百度百科.STL格式[EB/OL].https://baike.baidu.com/item/

　　[2]胡艳娥,诸进才,陈敏.数控加工精度在机检测技术研究现状[J].机床与液压,2021,49(16):168-173.

　　[3]白克,黎智,吴立辉.数控机床在机检测中触发式测头误差变速补偿[J].组合机床与自动化加工技术,2021(2):91-94.

　　[4]胡艳娥.数控加工精度在机检测技术及其误差修正技术研究[D].广州:广州大学,2020.

　　[5]胡艳娥,诸进才.一种在机检测触发式测头精度现场快速标定方法[J].机床与液压,2021,49(21):155-158.

　　[6]Taubin G.Estimating the tensor of curvature of a surface from apolyhedral approximation[C]//Fifth International Conference on

　　[7]神会存Computer Vision,1995.,周来水.基于离散曲率计算的三角网格模型优化调整[J].航空学报,2006(2):318-324.

关注SCI论文创作发表，寻求SCI论文修改润色、SCI论文代发表等服务支撑，请锁定SCI论文网！