SCI论文(www.lunwensci.com)
摘要:层析法作为实现三维全息成像的主要方法之一, 有着成像计算速度快、效果好的优点, 但是传统层析计算得到的像会存在 还原像层与层之间混叠的问题, 影响成像的质量。为解决使用层析法进行三维全息成像时导致的层间像混叠和串扰的问题, 提出 了一种优化方法, 基于 DMD 空间光调制器独特的微镜反射结构, 使用球面波为核心模拟全方向均匀衍射, 通过计算原始图像分层 衍射后的亚振幅全息图, 再使用 3D-GS 算法作为图像质量的优化方法, 并对优化结果进行分析, 通过仿真实验进行了验证。结果 表明提出的方法很好地解决了层析法计算全息三维重建像时层间混叠和串扰的问题, 同时, 相比于传统分层全息计算, 这种方法 在短距离衍射成像时具有更大的成像尺寸, 并且成像质量有了明显提高。
关键词:DMD空间光调制器,层析法,球面波,计算全息
Research on Solving Layered Holographic Imaging Aliasing Based on DMD Spatial Light Modulator
Zhang Hengchang, Zhang Ran, Fan Yuanyi, Zhang Tianyu, Chu Jinkui ※ (School of Mechanical Engineering, Dalian University of Technology, Dalian, Liaoning 116023. China)
Abstract: As one of the main methods for realizing 3D holographic imaging, tomography has the advantages of fast imaging calculation speed and good imaging quality. However, the image obtained by traditional tomographic calculation has the problem of overlapping between restored image layers, which affects the quality of imaging. To solve this problem, an optimization method was proposed. The method was based on the unique micro-mirror reflection structure of the DMD spatial light modulator. The spherical wave was the core to simulate the omnidirectional uniform diffraction. By calculating the sub-amplitude hologram after the layered diffraction of the original image, the 3D-GS algorithm was used as the optimization method of the image quality, and the optimization results were analyzed and verified by simulation experiments . The results show that this method can well solve the problems of inter-layer aliasing and crosstalk in 3D reconstruction images computed by tomography. At the same time, compared with the traditional layered holography calculation, this method has better performance in short- distance diffraction imaging, and imaging quality has been significantly improved.
Key words: DMD spatial light modulator; tomography; spherical wave; CGH
0 引言
随着光学成像技术的发展, 全息显示技术诞生, 并 成为了记录物波所携带的物体的强度信息与相位信息的 主要实现方式, 一直到激光器的发明和广泛应用, 光全 息显示技术得到了迅速的发展, 以其具有存储信息量大、 高对比度、制作成本低等优点, 在全息光刻[1-4]、信息存 储[5-6]、全息显影[7-8]等多方面都有着广泛的研究和应用。
随着数字计算机与计算技术的迅速发展, 人们广泛 地使用计算机模拟、运算、处理各种光学过程, 计算全 息技术的出现取代了使用传统的光学记录材料进行定影、 显影的操作的全息显示方式, 成为三维全息显示的主要 实现方式。现如今, 广泛使用的三维全息显示方法是通 过使用 SLM 空间光调制器加载通过计算机生成好的完全 记录目标 3D 物体的全波信息计算全息图, 经激光照射SLM 以还原目标图像的波前而得到全息像的方式。
三维计算全息图主要有点源法[9- 10]、层析法[11- 12]等生 成方式, 点源法的基本原理就是通过将目标三维物体看 做有限个点组成的集合, 物体的分辨率和组成该物体的 点集合的数量有关, 取点越多, 成像物体的还原程度和 细节越接近目标物体, 即成像质量越好。但是同样的点 的数量越多也使得在生成三维物体全息图的计算量越大, 对于结构复杂且点集合多的目标物体有时计算一张全息 图甚至需要数个小时的时间, 这显然不利于全息实时显 示的应用。所以很多的关于点源法的研究主要在提高其 计算效率上, 其中 1993 年, LUCENTE[13]提出基于查找表 ( LUT ) 加速全息图计算的方法, 通过预先采集点并存储 到计算机的方式来加快全息计算速度。之后, KIM 等[14] 在 LUT 的 基 础 上 利 用 空 域 卷 积 提 出 一 种 新 型 查 找 表( NGLUT) 法 和 新 加 坡 学 者 PAN 等[15] 提 出 分 离 查 找 表 ( SGLUT) 算法, 上述两种方法都对 LUT进行了优化进一 步降低了预设点所占用的计算机存储空间。同时随着计 算机技术的发展, 各种并行计算方式也成为了点源法提 高全息计算速度的主要方式。尽管点源法生成全息图的 速得到了很大的提高, 但是通过预存储占用大量计算机 存储空间和并行计算占用计算机的 CPU 资源的方式来提 高了生成全息图的速度, 对计算机的使用有了更高的要 求和消耗, 很大程度上限制了该方法使用。另一种是基 于多边形法的方法该方法在每个多边形的计算速度上和 计算点源法计算点的速度差不多[16], 所以多边形法在速 度上要优于点源法, 但是在多边形建模的过程中相比于 点源法要更加繁琐。而另一种基于层的方法, 是通过将 一个完整目标三维物体进行多层分割, 每一层的计算速 度都比较快, 还原物体的分辨力限制只有层数的多少。 这样该方法可以在保证图像质量的同时, 计算速度也很 快。但是, 层析法在对目标成像物体进行分层划分后, 实际就是对每一层的二维图进行全息计算, 计算生成的 平面全息图通过叠加就形成一幅需要的目标三维物体全 息图, 在还原后, 就会出现衍射造成分层混叠和图像串 扰的问题, 对成像质量造成很大的影响。所以解决该问 题对于提高三维全息成像质量有着重要的意义。
在本文中, 提出了一种应用球面波衍射为核心并使 用传统相位优化方法 GRECHBERG-SAXTON ( GS) 算 法[17]改进的优化方法 3D-GS相关算法[18-19]进行相位优化, 提升成像质量, 解决了使用层析进行全息成型后, 导致 的分层混叠和图像串扰的问题。该方法是在计算目标三 维物体时, 将三维物体首先解析成若干个平行平面。对 于每个分割图形平面中的每个像素, 都当作为空间中一 个发光物点, 该物点光波以球面波的形式发散传播到空 间距离 z 的位置平面处。同样的层析平面每个像素都看 做相似的形式进行计算。通过计算叠加就可以得到一个 距离层析物平面 z 距离处的衍射平面。该衍射平面通过 一束离轴干涉光照射, 就形成了一幅记录层析物平面全 部振幅信息的计算全息图, 对得到的计算全息图, 使用 GS算法经过多次迭代计算。就得到优化后的目标物体全 息图。通过仿真实验验证了该方法在解决分层成像混叠 串扰问题的可行性。
1 应用球面波迭代算法原理
1.1 球面波衍射理论方法
球面波的等相位面是球面, 通常情况下, 定义一个 空间点光源, 当该点光源与该点发出的球面波的中心重 合的时候, 可以得到光传播的球面波表达式为:
u (x,y,z,t) =cos ( k ⋅ r - 2πνt ) ( 1)
式中: u (x,y,z,t) 为光波传播到一定空间距离位置处光场强度; U0 为源光点的幅值大小, 是一个常数值; k 为波 矢; r 为光波传播的距离。
其中 r 可以表示为:
|r| = r =( 2)
如果球面波中心与源点重合, 光波沿着 z 轴方向进 行传播, 那么上式中的 z = z0. 通过相位因子表达式可以 知道, 当目标传播区域较小, 相对于实际研究区域的尺 度, 激光波长很小, r 的微小变化会引起相位的较大变 化, 所以 r 可以表示为:
|r| = |z0 | ≈ |z0 | + ( 3)
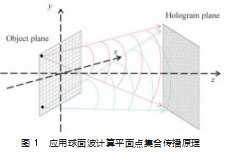
如 图 1 所 示, 球 面 光 波 传 播 到 z 距 离 的 平 面 一 点(xc ,yc ,zc ) 的时候, 球面波表达式为:
U (xc ,yc ,zc ) = exp(jk | zc - z0 |) ×exp(jk )
式中: U (xc ,yc ,zc ) 为光波在点 (x0 ,y0 ,z0) 处在空间传播到 点 (xc ,yc ,zc )处的球面波强度; U0 为目标位置的幅值大小; exp(jk |zc - z0 |)对光波场的相位不产生影响, 通常可以忽略。
使用式 (4) 计算单层目标图像干涉图样后, 为了形 成能够记录该图样的全部振幅信息, 还需要使用共轭参 考光束和源光波进行干涉, 干涉后形成的图像就得到了 完整的全息图。
得到全息图后, 就可以通过衍射计算得到相应的重建像, 这里假设衍射得到其中一个衍射平面的距离为 zi, 那 么 此 时 得 到 的 该 重 建 像 面 的 光 强 Uf (x,y,zi ),提取对应的迭代相位为 φi, 重新给原图像添加该对应 的相位:
U0 = U0 (cos ( φ i ) + j sin (φ i )) ( 5)
式中: U0 为初始振幅大小。
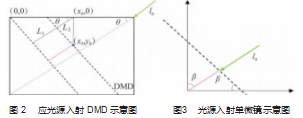
通过式 (5) 重建进行全息图的计算。上述即为完整 的迭代计算过程。球面波的使用可以充分利用 DMD 空间光调制器的衍 射原理, 使得经过空间光调制器微镜反射的光束在各个 方向的反射强度一致, 根据 DMD 空间光调制器的原理, DMD 芯片是由数百万个小微镜组成, 每个微镜呈对角线 进行偏转, 所以入射光线必须以 DMD 微镜对角线方向进 行入射, 所以对于参考光束如平面示意图如图 2~3 所示。
图 2 所示为 DMD 芯片及激光入射角度, 根据 DMD 芯片中微镜结构, 其中虚线所示为 DMD 芯片微镜的偏转对角线, 对于其中一个微镜设其平面坐标位置为 (x0 , y0 ),其中的 L 1 = x0 cos θ, L2 = y0 sin θ, 结合图 3 所示的单微 镜 光 线 入 射 示 意 图, 红 色 线 段 长 度 为 L = x0 cos θ - y0 sin θ。为了使得入射光照射在 DMD 芯片的每个微镜上 保持其入射光相位相同, 理想状态的入射光为平行光。 由于微镜位置及光线倾斜入射导致的相位差。因此可以 进行相应的计算相位投影为 L4 = sin β (x0 cos θ - y0 sin θ )。 所以参考光波可以由下式进行表示:
R(~) ( x, y ) = exp ( jk sin β (x0 cos θ - y0 sin θ ) ) ( 6 )
式中: R(~) ( x, y ) 为参考光波幅值; β 为微镜对角角度; θ 为 光波入射 DMD 芯片角度。
设物光场振幅的归一化值定义为参考光的振幅Ar 为:
U - Umin
Umax - Umin
式中: U 为全息面出的目标物体衍射光场; Umax 为衍射光 场最大值; Umin 为衍射光场最小值。
最后可以得到参考光波的最终表达式:
R(~) ( x, y ) = Ar exp ( jk sin β × ( x0 cos θ - y0 sin θ ) ) ( 8 )
通过调节光束比, 并使得参物光进行干涉, 于是在 全息图纪录面上的光强为:
I (x, y ) = | R(~) ( x, y ) + U (x, y )|2 ( 9 )
式中: I (x, y ) 为参物光干涉后的光强; R(~) ( x, y ) 为参考光 幅值大小; U (x, y ) 为光幅值大小。
通过干涉就可以最终形成记录有原始物体全部振幅 及相位信息的平面全息图。
相比于平面波计算, 使用球面波在进行全息计算和 再现时, 一就是对于成像大小方面, 参考光和源点光都 为平面波时, 只能改变像光波的方向, 即改变像的位置; 若为球面波, 就可以改变像光波的曲率, 即改变像的大小。二是该算法生成的全息图的还原像不存在其他级次 的衍射干扰像。三是在使用球面波进行衍射成像时, 在 成像距离较近并且成像面较小时, 球面波衍射形成的全 息成像质量相比于平面波更加出色。
1.2 3D-GS 算法应用原理
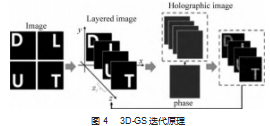
在成型图像优化上, 使用了 3D-GS 算法, GS 算法是 用于求解相位全息图的一种方法, 通常使用该方法求解 逆源问题。所谓的逆源问题就是根据所期望的光场衍射 分布求出期望的相位原始分布的问题。 3D-GS 算法就是 使用 GS 的基本思想进行三维光场相位优化的一种方式。 图 4 所示为本文迭代优化原理图。
首先将三维目标图像进行分层处理, 针对于单层图像 赋予随机相位并使用球面波衍射计算出对应全息图,若干 单层全息图叠加就生成了目标全息图,并使用对应衍射方 式进行还原像计算,提取对应还原像的相位值做为初始单 层图像的相位, 重复上述计算过程, 完成迭代优化过程。
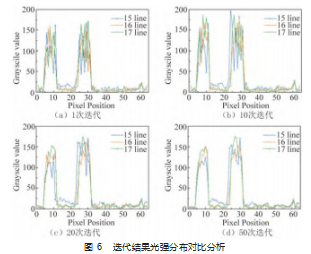
为了体现 GS 迭代的过程中对于还原图像的优化作 用。根据 3D-GS 算法原理进行单幅全息计算, 如图 5 所 示, (a)(b)(c) 分别为使用迭代计算的原始图像、全 息图以及重建像。图 6 则为在不同迭代次数下的图 5 中不 同还原图像部分像素行的灰度分布折线图。因为进行的是 振幅全息构建, 所以灰度在构建上等同于实际的光强表 现, 从图中可以看出, 随着迭代次数的增加, 在初始 1 次 迭代后生成的还原图的在第 15、16、17 行的灰度分布上 存在较大的数值波动, 相比之下在 50 迭代的情况下, 在 主要的成型区域部分, 灰度值已经区域整体稳定的状态。
2 球面波迭代算法仿真及结果分析
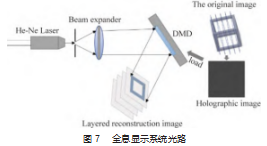
2.1 仿真实验光路及结果
图 7 所示为仿真系统实验光路图, 系统整体为不采 用透镜式全息成像系统。系统组成包括 532 nm 绿光激光 器作为源光源、扩束镜用于消除激光高斯干扰使得出射激光变成均匀的平行光束、DMD 空间光调制器使用的是最高 分辨率为 1 920 pix×1 080 pix 的 DLP 数字微镜 DMD 空间光 调制器, 该空间光调制器采用光强调制、通过配套的全息 图加载软件使用计算机用于将生成的好的计算全息图加载 到DMD 空间光调制器中、成像白板用于衍射还原像观察。为使用该算法加载图 8 中 4 张原始图片进行 20 次迭 代重建得到的还原图像, 如图 9 所示, 设定衍射距离为 d =50 mm, 全息图大小为 512 pix×512 pix, 还原像大小 为 64 pix×64 pix, 每张图片的间隔距离为 4 mm。通过还 原像可以看出, 使用该算法计算层析法生成的还原像在 各层之间的相互干扰和混叠较小, 还原像较为清晰。
2.2 仿真实验结果分析
对于层析法进行计算全息显示像时, 使用菲涅尔衍 射法在进行全息计算的时候, 其是存在 z 方向的最小传 播距离极限的限制:
2MΔ2z ≥
式中: Δx(2)为沿着 x 方向的采样周期; M 为 x 方向上的采样 数; λ 0 为波长。
式 (10) 为采用菲涅尔法计算衍射场的 z 方向传播 距离极限公式, 超过该距离时就会因为混叠效应产生误 差, 影响成像质量。由上述仿真结果可以看出, 球面波 迭代算法求解方式则不存在相应的限制。在更短衍射距 离位置处, 重建像质量仍然有较好的表现。
此外, 使用本文的方法在进行短距离成像显示时, 可以获得较大像面的清晰像。对于使用菲涅尔方式计算 的情况下, 其生成的最大还原像面为:
N λdx max Lx0
式中: Nx 为 x 方向上的采样点数; λ 为波长; d 为衍射距 离; Lx0 为物面实际空间长度。
由式 (11) 可知, 该菲涅尔算法主要适用于预设距 离 d 较大的情况。相对于本文提出的方法则可以实现在 短距离大尺寸成像, 如图 10 所示, 为使用球面波迭代算法的方式生成的不同大小的全息图的还原像。其中全息 图 的 大 小 为 512 pix×512 pix, 光 源 为 绿 光 光 源 波 长 为 532 nm。衍射距离为 30 mm, 提供过改变还原像面的尺 寸分别进行全息计算由图 10所示, 可以看到, 这样的近 距离衍射成像的情况下, 形成的重建像的长宽尺寸可以 实 现 在 150 mm 以 上 依 然 能 够 保 持 良 好 的 清 晰 度 。在 200~300 mm长宽大小尺寸时依然可以得到仅仅是边缘模 糊的重建像。相比于菲涅尔衍射实现的全息重建像存在 的大小限制和其适用于较远距离成像的特点, 本文提出 的全息算法在重建像大小范围上表现出更好的重建性能。
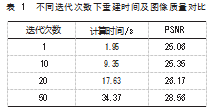
同时为了提高该算法计算速度, 使用了 CPU 多核并 行计算方式, 在本文仿真实验中, 使用并行计算环境为 Inter i9-2080RTX 的计算机, 支持最大并行计算数为 48 线程, 如表 1所示, 该算法进行不同的程度的迭代次数 下获得还原像所需时间及重建图像质量的对比, 其中衍 射距离 50 mm, 还原像面大小 64 pix×64 pix、全息图大小 512 pix×512 pix 固定不变。通过在不同迭代次数下重建 时间对比可以了解到, 使用并行计算的情况下, 在多迭 代次数下进行全息计算提升速度效果显著。同时通过图 像质量评价指标 PSNR值可以得到随着迭代次数的增加,PSNR值逐渐增大, 表示重建像质量也会有所提高。
3 结束语
本文提出了一种基于 DMD空间光调制器微镜结构并 使用球面波衍射配合 3D-GS相位优化的三维全息显示方 案, 该方法优化了三维全息显示方法中的传统层析法进 行三维像重建后各层还原像之间可能会出现的层间像串 扰和混叠的问题, 相比于菲涅尔及傅里叶求解方式相比, 还原像显示不需要进行复杂的衍射干扰像处理。仿真实 验结果表明, 本文提出的方法在进行三维全息显示重建 后不仅能够解决分层还原像出现层间串扰和混叠的问题, 同时能够在较大范围还原像面尺寸上保持良好的成像质 量。并且该种方法的实验光路组成简单, 实现方便, 为 层析三维全息显示的研究提供一种良好的解决方案。
参考文献:
[1] RUI H. Development of an autofocusing system using an electri ⁃ cally tunable lens in large area holographic lithography[J]. Ap⁃ plied Optics,2020.59(8):2521-2529.
[2] XUE G P. Polarized holographic lithography system for high-uni ⁃ formity microscale patterning with periodic tunability[J]. Micro⁃systems & Nanoengineering,2021.7(1):31.
[3] JUN H M,SHU Y. Creating Three-Dimensional Polymeric Micro ⁃ structures by Multi Beam Interference Lithography[J]. Journal of Macromolecular Science,Part C,2005.45(4):351-373.
[4] JEON T, KIM D H, PARK S G. Holographic fabrication of 3D nanostructures[J]. Adv. Mater. Interfaces,2018(5):1-13.
[5] 王欣浓 .基于等离激元光谱调控的 Ag/TiO_2 复合膜全息存储 研究[D]. 长春:东北师范大学,2020.
[6] 苏文静,胡巧,赵苗,等 . 光存储技术发展现状及展望[J]. 光电工 程,2019.46(3):4-10.
[7] 苏衍峰 . 基于空间光调制器的动态全息三维显示技术研究 [D]. 苏州:苏州大学,2019.
[8] GAO Q, LIU J, DUAN X, et al. Compact see-through 3D head⁃ mounted display based on wavefront modulation with holographic grating filter[J]. Opt. 2017.25(7):8412-8424.
[9] TSANG P W M,POON T C,WU Y M. Revies of fast methods for point-based computer generated holography[J]. Photontics Re⁃ search,2018.6(9):837-846.
[10] 金晓宇,桂进斌,刘超,等 .基于点源模型计算全息图快速生成 算法的研究进展[J].激光与光电子学进展,2018.55(10):48-57.
[11] GILLES A,GIOIA P. Real-time layer-based computer-generat⁃ ed hologram calculation for the Fourier transform optical system [J]. Applied optics,2018.57(29):8508-8517.
[12] SUN P. Holographic three-dimensional display based on opti ⁃ mizing arrangement of holograms[J]. Optics Communications, 2020.461(C):125260.
[13] LUCENTE M E. Interactive computation of holograms using a look-up table[J]. Journal of Electronic Imaging,1993.2(1):28-34.
[14] KIM S C,KIM E S. Effective generation of digital holograms of three-dimensional objects using a novel look-up table method [J]. Applied optics,2008.47(19):55-62.
[15] PAN Y C et al. Fast CGH computation using S-LUT on GPU[J]. Optics express,2009.17(21):43-55.
[16] MATSUSHIM K, NAKAHARA S. Extremely high-definition full-parallax computer-generated hologram created by the poly ⁃ gon-based method[J]. Appl. Opt.,2009(48):H54-H63.
[17] GERCHBERG R W,SAXTON W O. A practical algorithm for the determination of phase from image and diffraction plane pic ⁃ tures[J]. Optik,1972.35(2):237-246.
[18] WHYTE G,COURTIAL J,Experimental demonstration of holo ⁃ graphic three-dimensional light shaping using a Gerchberg- Saxton algorithm[J]. Phys.,2005(7):117.
[19] CHEN L,ZHANG H,HE Z,et al. Weighted Constraint Iterative Algorithm for Phase Hologram Generation. Applied Sciences[J]. Applied Science,2020(10):3652.
关注SCI论文创作发表,寻求SCI论文修改润色、SCI论文代发表等服务支撑,请锁定SCI论文网!
文章出自SCI论文网转载请注明出处:https://www.lunwensci.com/ligonglunwen/57778.html