SCI论文(www.lunwensci.com)
摘要 :针对目前偏振导航测试系统空间分辨率研究尚不完全的问题, 基于瑞利散射理论, 提出了一种偏振导航测试系统空间分辨 率计算方法, 搭建了天空偏振光空间分辨率仿真平台, 仿真分析了半球区域测试系统空间分辨率分布情况 。仿真结果表明: 太阳 直射点所在纬度线上, 偏振导航测试系统纬度分辨率远小于经度分辨率, 偏振导航测试系统受纬度波动影响较大; 太阳直射点所 在经度线上, 经度分辨率远小于纬度分辨率, 测试系统受经度波动影响较大 。非直射点经纬度线, 纬度值偏离直射点 10°~20°纬度 范围, 经纬度分辨率值比较接近, 测试系统受经纬度波动影响相差不大; 纬度值偏离直射点 30°~50°纬度范围, 经度分辨率小于纬 度分辨率, 测试系统受经度波动大于受纬度波动影响; 偏离直射点 50°以上纬度范围, 经度分辨率远小于纬度分辨率, 测试系统受 经度波动影响远大于受纬度波动影响。
关键词 :偏振导航,经度,纬度,瑞利散射,仿真
Research on Spatial Resolution of Polarization Navigation Test System Cui Yan, Liu Kang, Li Dexian, Zhou Ye
(Key Laboratory for Precision and Non-Traditional Machining Technology, Ministry of Education, Dalian University of Technology, Dalian,Liaoning 116024. China)
Abstract: In view of the current situation that the research on the spatial resolution of the polarization navigation test system is not complete , a method for calculating the spatial resolution of the polarization navigation test system was proposed based on the Rayleigh scattering theory , and the simulation platform for the spatial resolution of the polarized light in the sky was built . The distribution of longitude and latitude resolutions in the hemisphere was also analyzed. The simulation results showed that on the latitude line where the direct sun point was located , the latitude resolution was much smaller than the longitude resolution, and the test system was greatly affected by latitude; on the longitude line where the direct sun point was located, the longitude resolution was much smaller than the latitude resolution . The test system was greatly affected by longitude. On the latitude and longitude area where the non-direct beam point was located, deviating from the latitude range of 10°~ 20°of the direct beam point, the test system was basically the same as affected by latitude and longitude . Deviating from the latitude range of 30°~50°of the direct beam point, the longitude resolution was smaller than the latitude resolution, and the test system was more affected by the longitude fluctuation than by the latitude fluctuation. Longitude resolution was much smaller than latitude resolution and the test system was far more affected by longitude fluctuation than by latitude fluctuation when it deviated from the latitude range of more than 50° from the direct beam point.
Key words: polarization navigation; longitude; latitude; Rayleigh scattering; simulation
0 引言
在大自然中存在一种天空偏振光分布模式[1-2], 具有 不受外界干扰 、误差不随时间累积等优点 。基于该原理 研制的偏振导航测试系统通过获取当前天空偏振光分布 模式图, 提取太阳子午线[3]信息, 并结合此时太阳方位 角最终实现导航功能 。为了提高偏振导航测试系统的精 确度, 需要建立普遍适用的空间域 、时间域误差模型[4], 空间分辨率[4]可以形象地描述偏振导航测试系统的空间 域误差值大小 。因此, 探究偏振导航测试系统的空间分 辨率分布关系对实现高精度导航至关重要。
国内外学者对其进行大量研究, Zittrell 等[5]通过注射 神经生物示踪剂进行昆虫大脑细胞识别, 论证了蝗虫通 过直接光照与天空偏振模式相结合的方式实现导航 。贺 晓雷等[6]提出了一种可以直接应用的太阳方位角求解公 式 。桂文胜等[7] 改进了太阳位置计算公式, 仿真分析了 不同纬度, 日出时刻 、 日出方位角 、 白天时长和正午太 阳高度角的变化规律 。Horváth 等[8]通过测试日出时天空 偏振模式变化情况, 探究了偏振度 、偏振方位角随太阳 高度角 、太阳方位角的变化关系 。Kreuter 等[9]利用带有 旋转偏振器的自动鱼眼相机系统测量了全天空偏振模式的分布 。朱志飞等[10]提出了一种基于瑞利散射的太阳自 主定位方法计算地理位置信息 。Cai J 等[11]针对偏振光导 航系统航向误差随纬度的增加而增加的情况, 提出一种 改进的偏振光导航辅助的快速测量算法 。现有研究主要 是优化太阳位置信息求解公式, 以及如何获取更高精度 的地理位置信息, 实现高精度导航。
本文基于瑞利散射理论, 提出了经度分辨率和纬度 分辨率的概念, 描述偏振导航测试系统的空间分辨率 。 搭建了天空偏振光空间分辨率仿真平台, 逐一分析了半 球区域经度分辨率和纬度分辨率分布规律, 建立了偏振 导航测试系统空间分辨率分布模型。
1 基本原理
1.1 偏振导航测试系统仿真原理
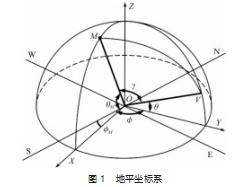
随着地球绕太阳周期性的自转和公转, 太阳光照射 到地球表面物体的角度也有所不同 。理想大气条件下, 基于瑞利散射理论, 构建地平坐标系如图 1 所示, 描述 太阳光在大气中单次散射过程 。O 点为当前观测者所处 地理位置点, N 、E 、S 、W 分别为正北 、正东 、正南和 正西方向, XOY 平面即代表观测者所处的地平面, Z 表 示天顶点, M 表示此时太阳所处位置 。太阳 M 同地平面 的夹角 θM 即所求太阳高度角, 水平面向上为正, 向下为 负; MO 所在直线在 XOY平面的投影同正南方向夹角 ϕM 即所求太阳方位角, 从正南向西为正, 向东为负 。V 为 天空中任一被观测粒子所处位置, θ 为其观测高度角, ϕ 为其观测方位角 。此时太阳位置坐标 (θM, qM ), 粒子坐 标 ( r,f, q ), r 为地平坐标系球半径。
任一时刻 、任一经纬度地区太阳高度角 、太阳方位 角可以通过下式计算获得[12]:
sin θM = sin φ sin δ + cos φ cos δ cos Ω ( 1 )
cos ϕM = (sin θM sin φ - sin δ) / (cos θM cos φ ) ( 2 )
式中: φ 为纬度; W 为太阳时角; d 为太阳赤纬角。
太阳时角 、太阳赤纬角可通过查阅天文年历获得, 为了便于实际应用和编程分析, 可以采用张闯等[13]提出 的方法进行计算 。基于瑞利散射理论, 根据几何关系可 得被观测点处偏振方位角 c 为:
sin θ cos θM - cos θ cos(ϕ - ϕM ) sin θM
tanχ = sin ( ϕ - ϕM ) sin θM
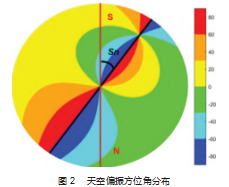
天空各点的偏振方位角值, 投影至 XOY平面, 组成 天空偏振方位角分布图如图 2 所示 。 图中黑色直线即太 阳子午线[3], 红色直线为体轴方向 (此时为南北方向), 太阳子午线与体轴方向夹角 sn 为导航参考角[14]。
在基于瑞利散射的理想大气模式下, 如图 2 所示的 天空偏振方位角分布图关于太阳子午线呈对称关系, 太 阳子午线所在区域的偏振方位角为±90°, 利用最小二乘 法对偏振方位角值为[60°, 90°]U[-60°, -90°]样本点区域 进行直线拟合, 由直线斜率获取导航参考角值。
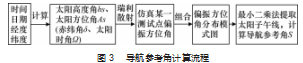
因此, 导航参考角可通过如图 3 所示流程图计算获 得 。偏振导航测试系统通过获取当前导航参考角, 结合 当前太阳方位角, 两者相减可得体轴同南北方向夹角即 当前朝向方向, 实现导航。
1.2 天空偏振光空间分辨率仿真平台原理
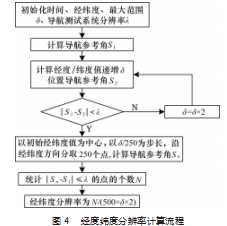
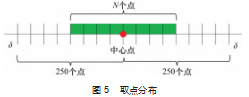
为了实现偏振导航测试系统高精度测量, 需要对其 在特定的时间域 、空间域进行测量误差分析, 本文提出 了偏振导航测试系统经度分辨率 、纬度分辨率的概念来 描述测试系统的空间域误差大小 。经度分辨率即纬度不 变, 经度变化一定范围, 偏振导航测试系统输出参数变 化量为其仪器分辨率 。纬度分辨率即经度不变, 纬度变 化一定范围, 偏振导航测试系统输出参数变化量为其仪 器分辨率 。 由此可通过经纬度分辨率这一变量值, 描述 空间域内偏振导航测试系统测量误差值 。某地理位置经 纬度分辨率越大, 表征该地理位置偏振导航测试系统经 纬度方向测量误差越大; 经纬度分辨率越小, 表征该地 理位置偏振导航测试系统经纬度方向测量误差越小 。 同 一时刻, 不同地理位置, 经度分辨率, 纬度分辨率值各 不相同 。 同时, 由于偏振导航测试系统输出参量即导航 角可以由导航参考角简单换算获得, 因此可以借由导航参考角的变化替代偏振导航测试系统输出参量的变化 。 为了探究经度变化率 、纬度变化率的分布规律, 本文提 出了如图 4 所示的经纬度分辨率计算方法。以经度分辨率为例, 为了计算某时刻某地理位置经 度分辨率, 初始设置时间 、 日期 、经纬度 、最大范围 d、 导航测试系统分辨率 l, 计算以该地理位置点为中心, 纬 度值不变, 经度值以最大范围 δ/250 度为步长, 经度方向 向东向西各取 250个点的导航参考角 Sn, 如图 5 所示。
统计 500个点中导航参考角同中心点导航角 S1 差值 小于导航测试系统分辨率 l 的点的个数N, 由下式可得中 心点处经度分辨率 T:
T=N/(500×δ ×2) ( 4 )
初始设置最大范围 δ =0.25. 步长为(δ /250) °, 因此 初始经纬度分辨率的最小值为 0.001° 。若初始步长过小, 系统时间复杂率较高, 若初试步长较大, 或初试最大范 围 δ过大, 计算所得经纬度分辨率精度过低, 综合考虑 设置该初试值 。若初始设置最大范围 δ过小, 可能存在 某一半取点的导航参考角值同中心点导航角差值均在导 航测试系统分辨率 0. 1°范围以内, 此时不能保证所计算 的纬度分辨率为真实分辨率, 故需提前计算纬度值增加/ 减少最大范围 δ处纬度的导航参考角, 若任一导航参考 角同中心点处导航参考角差值小于导航测试系统分辨率 λ, 则最大范围 δ增加 1 倍。
根据经纬度分辨率计算流程图, 搭建了天空偏振光 空间分辨率仿真平台, 如图 6 所示, 该仿真平台可以计 算任意日期 、时间 、经纬度地区的偏振导航测试系统的 经度分辨率和纬度分辨率。
2 仿真结果与分析
为了探究偏振导航测试系统空间分辨率分布规律, 利用天空偏振光空间分辨率仿真平台, 分别计算了半 球区域偏振导航测试系统的经度分辨率和纬度分辨率, 综合两者分布情况, 得出偏振导航测试系统空间域误 差大小 。
2.1 纬度分辨率分析
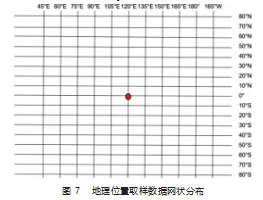
以 2022 年 3 月20 日 (春分日) 北京时间 12 时作为时 刻基准, 此时太阳的直射点在 0°纬线和东经 120°交汇 处 。 以该直射点为中心点, 分别向东 、 向西每隔 15°经 度 (一个时区) 取一个经度值; 分别向北 、 向南每隔 10°纬度取一个纬度值, 组成 11×17 个网状地理位置分布 点 。如图 7 所示, 中心红色圆点为此刻太阳直射点 。假 设此时偏振导航测试系统仪器分辨率为 0. 1° 。分别计算 各地理位置点纬度分辨率。
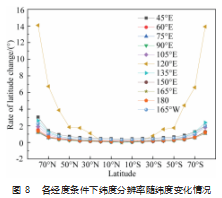
以纬度作为 X 轴, 纬度分辨率为 Y 轴, 绘制不同经 度条件下, 纬度分辨率随纬度变化情况, 如图 8 所示 。 由图可知, 同一经度条件下, 太阳直射点所在纬度即 0° 纬度的纬度分辨率最小, 向高纬度方向逐渐增大 。同时, 太阳直射点所在经度线即此时的东经 120°经度线上, 增 速明显高于非太阳直射点所在经线。
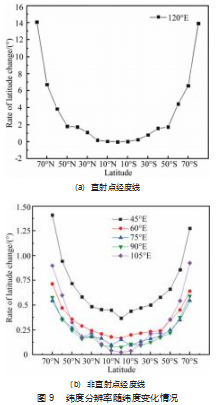
为了定量分析纬度分辨率的分布情况, 分别绘制直 射点经度 、与非直射点经度线上, 纬度分辨率随纬度变 化情况图 。如图 9 (a) 所示, 太阳直射点所在经度线, 0°~20°纬度区域, 纬度分辨率变化较缓, 纬度分辨率在 0°~0.2°; 20°~50°纬度区域, 纬度分辨率变化较为明显,纬度分辨率在 0.2°~2°; 50°以上纬度区域, 纬度分辨率 变化非常明显, 纬度分辨率在 2°以上。
由图 9 (b) 可得, 60°E~105°E 经度线上, 0°~20°纬 度区域, 纬度分辨率变化区间在 0°~0.2°; 20°~50°纬度 区域, 纬度分辨率变化区间在 0. 15°~0.4°; 50°以上纬度 区域, 纬度分辨率变化区间在 0.3°~1° 。75°经度线上, 0° ~20° 纬度区域, 纬度分辨率变化区间在 0.25° ~0.5°; 30°~50°纬度区域, 0.5°~0.75°; 50°以上纬度区域, 变化 区间在 0.75°~1.5°。
2.2 经度分辨率分析
同纬度分辨率分析一致, 以 2022 年 3 月20 日 (春分
日 ) 北京时间 12 时作为时刻基准, 取 11×17 个呈网状分
布的经纬度地理位置, 分别计算各地理位置点经度分辨 率 。并假设此时偏振导航测试系统仪器分辨率为 0. 1°。
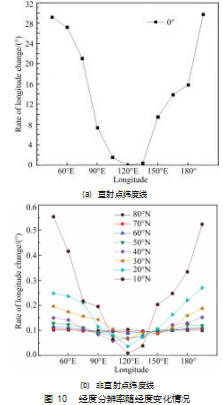
分别绘制直射点纬度线与非直射点纬度线经度分辨 率随经度变化情况如图 10 所示 。 由图可得, 随着经度值 向远离直射点两端偏移, 经度分辨率逐渐增大, 且越靠 近太阳直射点所在纬线上, 经度分辨率增大的速率越快。 由图 10 (a) 可得, 太阳直射点所在纬度线, 105° E~ 120°E 经度区域, 经度分辨率变化不太明显, 经度分辨 率分布在 0°~2°; 45°E~105°E 经度区域, 经度分辨率变 化十分明显, 经度分辨率分布在 2°以上 。 由图 10 (b) 可得, 30°及以上纬度区域, 经度分辨率变化区间在 0°~ 0.2°; 20° 纬度线上, 经度分辨率变化区间在 0° ~0.3°; 10°纬度线上, 经度分辨率变化区间在 0°~0.6°。
2.3 综合分析
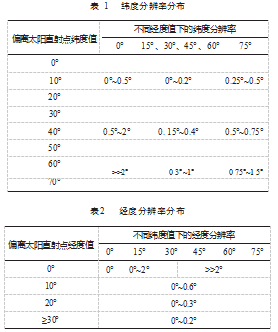
综合以上结论, 绘制当前时间, 全半球范围内纬度 分辨率分布表, 如表 1 所示, 首列首行分别为经纬度偏 离太阳直射点纬度 、经度值, 同一经度线上, 随着纬度 取值偏离直射点纬度, 纬度分辨率单调递增。
综合以上结论, 绘制当前时间全半球范围内经度分 辨率分布表如表 2 所示, 且同一纬度线上, 经度分辨率 随经度值增大单调递增; 同一经度线上, 经度变化 0°~ 15°区域, 经度分辨率随纬度值增大单调递增, 经度变化 30°以上区域, 经度分辨率随纬度值增大单调递减。
综合表 1 、表 2 可得, 太阳直射点所在纬度线上, 随 着经度取值逐渐偏离直射点经度, 纬度分辨率变化范围 在 0°~0.5°, 经度分辨率由 0°快速增加到远大于 2°, 纬度 分辨率远小于经度分辨率; 太阳直射点所在经度线上, 随着纬度值逐渐偏离直射点, 纬度分辨率由 0°快速增加 到远大于 2°, 经度分辨率变化范围在 0°~0. 1°, 经度分辨 率远小于纬度分辨率。
非直射点经纬度线, 纬度值偏离直射点 10°~20°纬度 范围, 经度分辨率变化范围在 0°~0.6°, 纬度分辨率在 0° ~0.5°, 经度分辨率 、纬度分辨率相差不大; 纬度值偏离 直射点 30°~50°纬度范围, 经度分辨率变化范围在 0°~ 0.2°, 纬度分辨率变化范围在 0. 15°~0.75°, 经度分辨率 小于纬度分辨率; 偏离直射点 50°以上纬度范围, 经度 分辨率变化范围在 0°~0.2°, 纬度分辨率在 0.3°~1.5°, 经 度分辨率远小于纬度分辨率用。
3 结束语
本文通过引入经纬度分辨率这一参考量, 描绘偏振 导航测试系统空间域误差大小, 通过控制变量法分别从 经度方向 、纬度方向探究偏振导航测试系统空间分辨率 分布规律 。结果表明: 太阳直射点所在纬度线上, 偏振 导航测试系统纬度分辨率远小于经度分辨率, 偏振导航 测试系统受纬度波动影响较大; 太阳直射点所在经度线 上, 经度分辨率远小于纬度分辨率, 测试系统受经度波 动影响较大 。非直射点经纬度线, 纬度值偏离直射点 10°~20°纬度范围, 经纬度分辨率值比较接近, 测试系统 受经纬度波动影响相差不大; 纬度值偏离直射点 30°~50° 纬度范围, 经度分辨率小于纬度分辨率, 测试系统受经度波动大于受纬度波动影响; 偏离直射点 50°以上纬度 范围, 经度分辨率远小于纬度分辨率, 测试系统受经度 波动影响远大于受纬度波动影响。
参考文献:
[1] Dacke M, Nilsson D E, Warrant E J, et al. Built-in polarizers form part of a compass organ in spiders[J]. Nature (London), 1999. 401(6752): 470-473.
[2] Muheim R, Phillips J B, Akesson S. Polarized Light Cues Under⁃ lie Compass Calibration in Migratory Songbirds[J]. Science (American Association for the Advancement of Science), 2006. 313(5788): 837-839.
[3] 晏磊, 关桂霞, 陈家斌,等 . 基于天空偏振光分布模式的仿生导 航定向机理初探[J]. 北京大学学报(自然科学版). 2009. 45(4): 616-620.
[4] 晏磊 . 偏振遥感物理[M]. 北京:科学出版社, 2014.
[5] Zittrell F, Pfeiffer K, Homberg U. Matched-filter coding of sky polarization results in an internal sun compass in the brain of the desert locust[J]. Proceedings of the National Academy of Scienc ⁃ es, 2020. 117(41): 25810-25817.
[6] 贺晓雷, 于贺军,李建英,等 . 太阳方位角的公式求解及其应用 [J]. 太阳能学报,2008(1):69-73.
[7] 桂文胜,李涛, 陆彦斌 . 太阳位置公式的改进及应用[J]. 水电能 源科学,2011.29(9): 213-216.
[8] Horváth G, Wehner R. Skylight polarization as perceived by des ⁃ ert ants and measured by video polarimetry[J]. Journal of Com⁃ parative Physiology A, 1999. 184(1): 1-7.
[9] Kreuter A, Emde C, Blumthaler M. Measuring the influence of aerosols and albedo on sky polarization[J]. Atmospheric Re⁃ search, 2010. 98(2-4): 363-367.
[10] 朱志飞,杨江涛,王晨光,等 . 基于瑞利大气偏振模式的太阳自 主定位方法及其实现[J]. 激光与光电子学进展, 2017. 54(2): 306-310.
[11] Cai J, Cheng J, Liu J, et al. A Polar Rapid Transfer Alignment Assisted by the Improved Polarized-Light Navigation[J]. IEEE Sensors Journal, 2022. 22(3): 2508-2517.
[12] 王国安,米鸿涛,邓天宏,等 . 太阳高度角和日出日落时刻太阳 方位角一年变化范围的计算[J]. 气象与环境科学 , 2007. 30 (Z1): 161- 164.
[13] 张闯, 吕东辉,顼超静 . 太阳实时位置计算及在图像光照方向 中的应用[J]. 电子测量技术, 2010. 33(11): 87-89.
[14] 李世奇 . 基于天空偏振光场的成像式航向测量系统研究[D]. 大连:大连理工大学, 2019.
关注SCI论文创作发表,寻求SCI论文修改润色、SCI论文代发表等服务支撑,请锁定SCI论文网!
文章出自SCI论文网转载请注明出处:https://www.lunwensci.com/ligonglunwen/57152.html