基于深度学习神经网络的油气管道漏磁检测缺陷诊断论文

SCI论文（www.lunwensci.com）

　　摘要： 管道缺陷尺寸预测时， 由于管道漏磁数据量庞大以及常规预测方法精度不高， 提出一种基于迁移学习的改进型卷积神经网络与贝叶斯优化算法， 以预测管道缺陷尺寸。将已训练好的 Lenet 网络进行迁移， 对迁移后的网络结构进行重构， 建立了 TB-CNN 改 进型网络。提出了改进型神经网络的贝叶斯优化算法， 对迁移学习改进后的模型的训练过程进行超参数优化， 得到最优的 TB-CNN模型。在制作训练集时， 提出了格拉姆角场 (GAF) 算法将一 维的漏磁曲线数据转换为二 维图像方法。通过仿真及实验， 证明了该网络对长度和宽度为 10 ~40 mm 范围 、深度在 2 ~ 10 mm 范围的缺陷预测均方误差根 (RMSE) 为 0.069 1. 和其他网络相比， 该方法对管道缺陷尺寸的预测精度更高。

　　关键词： 管道缺陷,卷积神经网络,迁移学习,贝叶斯优化,格拉姆角场


　　Abstract：When predicting the size of pipeline defects，due to the huge amount of pipeline magnetic flux leakage data and the low precision ofconventional prediction methods，an improved convolution neural network and Bayesian optimization algorithm based on transfer learning wasproposed to predict the size of pipeline defects.The trained Lenet network was migrated，the migrated network structure was reconstructed，and an improved TB-CNN network was established.The Bayesian optimization algorithm of improved neural network was proposed，and the training process of the improved model of transfer learning was super-parametric optimized to obtain the optimal TB-CNN model.When making the training set，the Gram Angular Field(GAF) algorithm was proposed to convert the one-dimensional magnetic flux leakage curve data into two- dimensional images.Through simulation and experiment，it is proved that the RMSE of this network is 0.0691 for the defects with length and width ranging from 10 mm to 40 mm and depth ranging from 2 mm to 10 mm.Compared with other networks，this method has higher prediction accuracy for pipeline defects.

　　Key words：pipeline defect;CNN;transfer learning;Bayesian optimization;Gram angle field


　　0 引言

　　石油 、天然气通常会用油气管道运输， 但随着使用时间的增加， 由于磨损 、腐蚀 、意外损伤等原因会导致 管 道 产 生 缺 陷 [ 1] 。 漏 磁 检 测 ( Magnetic Flux Leakage， MFL) [ 2-5 ] 是一种被广泛的应用于检测长输油管道缺陷的无损检测方式， 通过对管道缺陷进行漏磁检测试验采集数据， 从而为管道的缺陷识别、检修、维护等提供可靠参考。

　　目前， 管道缺陷尺寸的预测方式主要通过管道漏磁 检测数据中的径向漏磁分量和轴向漏磁分量进行数据图 像可视化， 根据漏磁一维图像特征对管道缺陷尺寸进行 预测。 由于直接通过人工来进行管道缺陷尺寸识别， 非 常费时费力， 且管道缺陷识别准确率大多依靠工程师的 经验而定， 所以智能检测管道缺陷方法应运而生。 国内 对于管道缺陷的智能检测[ 6 ]， 主要应用的神经网络方法有 BP 神经网络 、RBF 神 经 网 络 、支 持 向 量 机[ 7-9 ] 等。国外对于焊接缺陷数据进行训练和识别主要应用的方法 为多层感知器神经网络[ 10 ] 。这些方法大都建立在一维的 漏磁信号特征基础上， 缺少其他维度的特征信息， 且信 号特征提取信息有限， 导致缺陷预测结果误差较大， 且精度不 高。 据 此， 本 文 提 出 一 种 基 于 改 进 的 迁 移 学习 [ 11 -12 ] 的 Lenet 卷积神经网络模型 TB-CNN， 并且将此 模型进行贝叶斯优化[ 13 ]， 最终得到最优的 TB-CNN 模 型对管道漏磁图像进行训练， 通过向最优 TB-CNN 模型输入仿真和实验数据进行训练， 建立管道漏磁缺陷尺寸预测系统， 从而提升管道缺陷尺寸预测效率以及准确性 。

　　1 TB-CNN 神经网络结构研究

　　1.1 漏磁曲线的特点

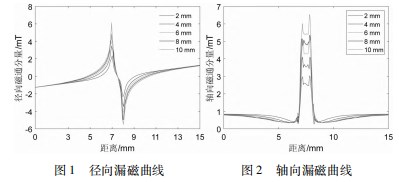
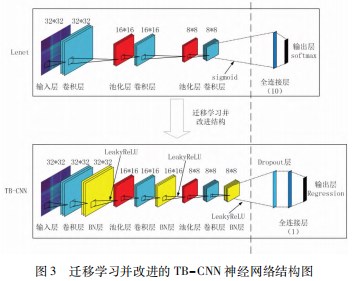
　　本实验所涉及到的管道漏磁信号[14] 包括两种： 径向漏磁信号和轴向漏磁信号。如图 1 、2 所示， 通过改变缺 陷的尺寸， 得出管道缺陷在不同尺寸下的漏磁场分布规 律。在相同宽度的条件下， 随着缺陷深度增加， 缺陷的 径向漏磁分量 、轴向漏磁分量的峰值明显增大; 在相同 深度下， 缺陷的径向漏磁分量的正负极值间距随着宽度 增加而增大， 轴向漏磁分量谷间距随着宽度增加而增 大 [ 15] 。图 1 、2 中， 控制长度 、宽度不变， 只改变缺陷 深度时， 径向和轴向漏磁分量的变化规律。


　　1.2 基于迁移学习改进的卷积神经网络模型

　　考虑深度学习模型从零开始训练需要大量数据 、相 当大的计算成本和时间成本， 而实际仿真模型的漏磁数 据较少， 应用实验数据很难训练出实际可行的网络模型。 迁移学习能减少神经网络模型对数据量的依赖。 因此， 采用已经训练好的 Lenet 网络模型， 通过迁移学习将预 训练模型的网络结构 、模型参数转移到改进的神经网络 模型上， 从而实现对管道漏磁缺陷尺寸的预测。

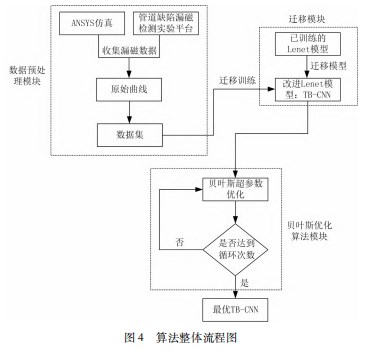
　　在迁移学习过程中， 对 Lenet 卷积神经网络模型进 一步优化， 主要包括： (1) 添加批量归一化层[ 16 ]， 可 以加速卷积神经网络的训练; (2) 添加 Dropout 层， 有 效地改变了迭代之间的底层网络架构， 有助于防止网络 过度拟合; (3) 将原 ReLU 激活函数改进成 leaky ReLU 函数。再向卷积层导入已经训练好的权重与参数， 然后用新设计的全连接层代替原本的全连接层， 组成新的卷积网络模型 TB-CNN， 最后用仿真和实验数据训练新模 型。改进的 TB-CNN 模型如图 3 所示。


　　改进的卷积神经网络的具体结构主要包括 1 个输入层， 3 个卷积层 、3 个批量归一化层 、2 个池化层 、1 个 Dropout 层 、1 个全连接回归层和 1 个输出层。采用 Leaky ReLU 函数作为网络层级之间的激活函数。

　　(1) 卷积层

　　假设其位于网络的第 l 层， 则其输出为：

　　(5) Dropout 层

　　Dropout 的直接作用是减少中间特征的数量， 从而减 少冗余， 即增加每层各个特征之间的正交性。在每个训 练批次中， 通过忽略一半数量的特征检测器 (让一半的 隐层节点值为 0)， 可以明显地减少过拟合现象。

　　(6) 目标函数

　　选取均方根误差 ( Root Mean Squared Error， RMSE) 作为回归预测模型的结果精度指标， 如式 (9 ) 所示。 将其作进一步改进： 添加 L2 正则化项优化。它在保证训 练误差尽量小的同时自动调节参数， 优化网络结构， 同 时尽量 减 小 有 效 权 值， 提 高 网 络 的 泛 化 能 力， 如 式 (10) 所示。


　　2 TB-CNN 贝叶斯优化的算法

　　2.1 优化算法

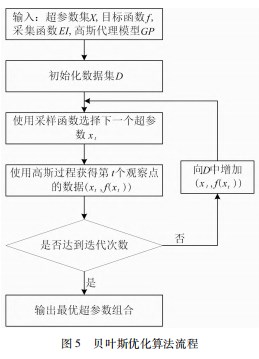
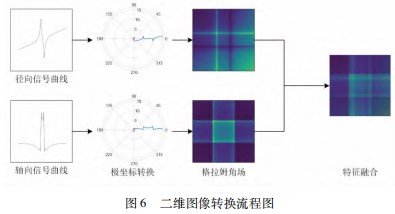
　　具体流程包括： 数据预处理 、迁移学习和贝叶斯超 参数优化[ 17-20 ] 。算法整体框架如图 4 所示。通过 ANSYS仿真和实验平台收集漏磁数据。对数据进行预处理主要 包括： 将数据叠加合理大小的噪声， 来对数据集进行扩 充。用格拉姆角场 (GAF) 算法将一维漏磁数据变换成二维图像， 并且将径向漏磁分量和轴向漏磁分量的图像进行特征融合。然后将 Lenet 模型进行迁移改进为 TB- CNN 。考虑 TB-CNN 模型的超参数对管道缺陷识别预测 结果 的 影 响， 使 用 贝叶 斯 优 化 对 TB-CNN 的 学 习 率、SGDM 的动量以及正则化强度进行超参数优化。


　　2.2 训练过程的贝叶斯优化

　　TB-CNN 模型的学习率 η和 SGDM 的动量 monentum的选取影响网络训练速度; 合适的正则化系数 λ可以很 好解决过拟合问题。若采用手动调参， 过程复杂， 且难以得到最优模型。 因此本文使用了贝叶斯优化算法优化TB-CNN 的超参数。 贝叶斯优化算法只需要经过有限次参数寻优 就 可 以 获 得 较 优 的 网 络 模 型。其 流 程 如 图 5 所示。


　　2.2.1 贝叶斯优化原理

　　贝叶斯优化算法根据贝叶斯定理来估计目标函数的 后验分布式， 然后通过对未知的目标函数过去评估结果 建立替代函数， 寻找下一个最小化目标函数值的超参数


　　2.2.3 采集函数

　　采集函数的作用是确定下一个需要评价的点 xt 。使用 EI (Expected Improvement) 来确定下一次迭代的超参 数 xt 。在第 t 次迭代中，EI 的定义域是未遍历的区域的 集合以及目前已观测到的所有目标函数中最优结果对应 的 xt 的集合。最大化采集函数 EI ( x ) 的 x 就是被选取 的下一个超参数取值：


　　3 仿真及实验

　　3.1 数据采集

　　使用 ANSYS MAXWELL 有限元仿真软件搭建管道缺 陷漏磁检测模型，为后面基于深度学习神经网络管道缺 陷检测系统的设计与缺陷尺寸的预测提供数据。为进一 步验证本文提出的方法在实际工程中的有效性，利用管 道缺陷漏磁检测实验平台得到现场缺陷漏磁数据。选取 直径 203 mm 、壁厚 10 mm 、长 1 m 的管道，采用人工方 式制作管道缺陷，利用霍尔传感器来检测漏磁数据，并 搭建实验台框架。最终收集到长度 10 ~ 40 mm ，宽度 10 ~40 mm ，深度 2 ~ 10 mm 范围的缺陷尺寸数据。

　　3.2 数据预处理

　　对漏磁数据添加各类噪声，将数据集进行数据增强 操作，将漏磁数 据 扩 充 至 10 000 份。用 格 拉姆 角 场 (GAF) 算法将一维漏磁数据进行二维变换。由于需要径 向和轴向漏磁数据同时输入，为了提升训练效率，将径 向和轴向漏磁数据的二维图像进行特征融合，并设置大 小为 32 *32 像素，如图 6 所示。


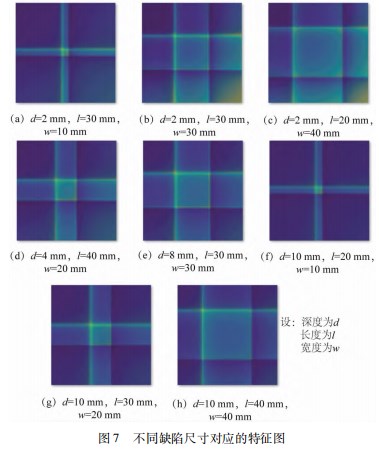
　　建立基于卷积神经网络的管道漏磁曲线图像数据集 ，每种缺陷的特征图像素大小为 32 *32 。将数据集 按照 9∶1 的比例随机划分成训练集和测试集。图 7 为随机选取不同特征图所对应缺陷的尺寸。

　　3.3 贝叶斯优化过程

　　(1) 选取适当网络的初始学习率 LR 。

　　(2) 选取合适的随机梯度下降的动量 MT 。

　　(3) 选取合适的 L2 正则化系数 λ。


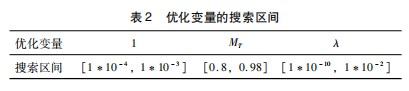
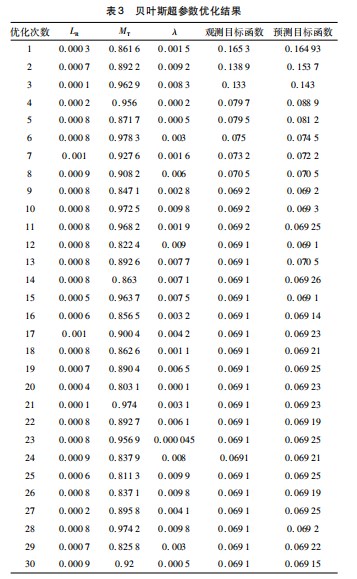
　　上述 3 个参数相互影响， 任意一个参数的变动都会导致其余参数对 TB-CNN 的最终效果产生变化， 因此需 要找到全局最优的参数组合。将数据集输入 TB-CNN 模型， 并使用贝叶斯优化算法对超参数进行选择， 设置最 大迭代次数为 30. 在参数范围的设置上， 根据文献[21] 和经验确定优化变量的搜索区间， 具体各项变量范围如表 2 所示。 由表 3 可知， 经过 30 次的迭代， 第 12 次优化模型得到的 RMSE 最低， 为 0.069 1 。最终确定网络的 初始学习率 LR =0.000 8. 随机梯度下降的动量 MT = 0.822 4. L2 正则化系数 λ=0.009 。


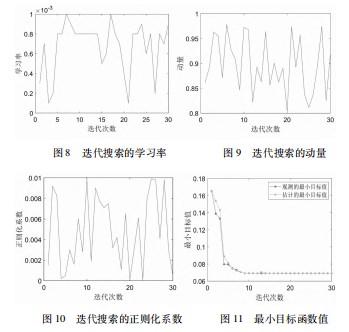
　　图 8 ~ 10 为贝叶斯优化过程中所搜索的参数曲线。 图 11 为贝叶斯优化结果曲线， 从图中可以看出当迭代至 12 次之后曲线逐渐收敛， 此时表明贝叶斯已迭代至最 佳， 接下来的计算已经无法再改善目标函数， 说明全局最优已经找到。


　　3.4 优化后的性能比较

　　为了验证贝叶斯优化算法对 TB-CNN 模型结果的影响， 设立未优化的模型， 其结构与经过贝叶斯优化的 TB-CNN 的结构保持相同， 选择默认的神经网络超参数， 即 LR =0.01. MT =0.8. λ=0.000 1 。得到的 RMSE 对比结果如表 4 所示。从表中可以看出， 与无贝叶斯优化的 TB-CNN 相比， 经过贝叶斯优化的 TB-CNN 预测更为精准。


　　3.5 实验结果

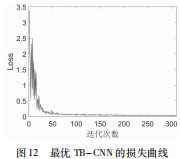
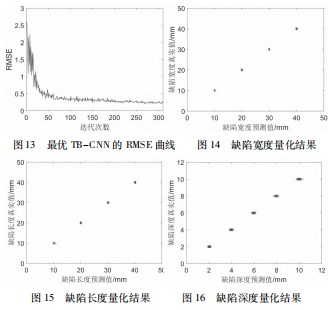
　　将经过贝叶斯优化之后的最优 TB-CNN 模型保存，并输入测试集进行测试， 其损失值曲线和 RMSE 曲线如图 12 和 13 所示。从图 中可以明显观察到， 当 迭代到 300 次后， 网络 的损失值和 RMSE 趋于 稳定。如 图 14 ~ 16 所 示为最终预测管道缺陷 的 长 度 、 宽 度 、 深 度 结果。


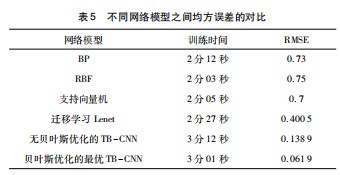
　　为验证本文算法的有效性， 将优化模型和传统神经 网络进行对比， 如表 5 所示。 由表可知， 未优化的 CNN 缺陷尺寸预测误差大， 因此对其进行优化具有必要性。 经过利用贝叶斯优化算法优化迁移学习改进的神经网络 结构对于管道缺陷的预测更为精确， 明显优于未优化的 CNN 模型。


　　4 结束语

　　针对人工判定管道缺陷效率低， 和浅层网络对于管道缺陷尺寸预测精度不高等问题， 提出利用一种基于迁移学习的改进卷积神经网络模型： TB-CNN 。改进的 TB -CNN 模型中利用批量归一化来提高模型训练速度， 添加dropout 层来防止过拟合， 且为了避免可能出现的神经元 “死亡”现象， 将激活函数 ReLU 改进为 Leaky ReLU 。

　　并且由于人工搜索超参数难以找到最优组合， 提 出利用贝叶斯优化算法 自动寻找最优超参数组合的方 法 。利用贝叶斯优化算法在 30 次迭代中成功地找到了最优的网络结构和超参数组合： 网络的初始学习率为0.000 8; 随机梯度下降的动量为 0.822 4; L2 正则化系数 λ=0.009 。


　　相比于传统卷积神经网络， TB-CNN 方法具有更加精准的管道缺陷尺寸预测能力以及训练效率， 其综合预测均方根误差低至 0.069 1 。结果表明， 本文提出的方法为油气管道漏磁检测缺陷预测提供了一种综合性能更好的思路。

　　参考文献：

　　[1]杨理践，曹辉.基于深度学习的管道焊缝法兰组件识别方法 [J].仪器仪表学报，2018.39(2)：193-202.

　　[2]许宇帆，贾银亮，张润华，等.基于相关性的钢轨缺陷漏磁检 测提离干扰抑制[J].电子测量技术，2022.45(4)：147-152.

　　[3]张雪伟，陈金忠，康小伟，等.油气管道划痕非饱和漏磁检测 与识别[J].石油机械，2022.50(03)：132-138.

　　[4]卢森骧，神祥凯，张俊楠，等.基于三轴融合的漏磁内检测数据缺 陷反演方法研究[J].仪器仪表学报，2021.42(12)：245-253.

　　[5]岳明星，杨理践，石萌.基于卷积神经网络的管道漏磁内检测 焊缝识别方法[J].电子世界，2018(12)：49-50.

　　[6] Liu Shucong，Wang Hongjun，Li Rui.Attention Module Magnetic Flux Leakage Linked Deep Residual Network for Pipeline In- Line Inspection [J].Sensors，2022.22(6)：2230.

　　[7]田凯，孙永泰，高慧，等.贝叶斯算法 BP 神经网络缺陷量化研 究[J]. 中国测试，2014.40(3)：93-97.

　　[8] 曾维国，李曙华，李岩，等.基于径向基函数神经网络预测模 型评价油气水集输管道的均匀腐蚀缺陷[ J].腐蚀与防护， 2020.41(10)：50-56.

　　[9]彭丽莎，黄松岭，赵伟，等.漏磁检测中的缺陷重构方法[ J]. 电测与仪表，2015.52(13)：1-6.

　　[10] Lim T Y，Ratnam M M，Khalid M A.Automatic classification ofweld defects using simulated data and an MLP neural network[J].INSIGHT，2007.49(3)：154-159 .

　　[11]谢锋云，董建坤，符羽，等.迁移学习和 CNN 的电机故障诊断方法[J/OL].机械科学与技术：1-7[2022-09-26] .

　　[12] Liu Yiwen，Zhang Xian，Gao Yanxia，et al. Improved CNNMethod for Crop Pest Identification Based on Transfer Learning[J].Computational Intelligence and Neuroscience，2022.2022： 9709648.

　　[13] Atteia Ghada，Alhussan Amel A，Samee Nagwan Abdel.BO- ALLCNN： Bayesian-Based Optimized CNN for AcuteLymphoblastic Leukemia Detection in Microscopic Blood SmearImages.[J].Sensors (Basel，Switzerland)，2022.22(15)：5520.

　　[14] Hu Bing，Zhang Ning，Wang Lu，et al.Simulation Analysis ofMagnetic Flux Leakage Detection Damage of Natural GasPipelines [J].IOP Conference Series：Earth and EnvironmentalScience，2021.804(2).

　　[15]苏林，成文峰，许志军，等.油气管道缺陷漏磁检测有限元模拟[J].焊管，2020.43(4)：8-13.

　　[16 ] Zhijie Yang，Lei Wang，Li Luo，et al. Bactran：A HardwareBatch Normalization Implementation for CNN Training Engine[J].IEEE Embedded Systems Letters，2020：1.

　　[17]Aaron Klein，Stefan Falkner，Simon Bartels，et al.Fast Bayesianhyperparameter optimization on large datasets [ J ]. ElectronicJournal of Statistics，2017.11(2)：4945-4968.

　　[18] Shang Qiang，Feng Linlin，Gao Song. A Hybrid Method for Traffic Incident Detection Using Random Forest - Recursive Feature Elimination and Long Short -Term Memory Network With Bayesian Optimization Algorithm [ J ]. IEEE ACCESS，2021.9：1219-1232.

　　[19]Zulfiqar M， Gamage Kelum A A， Kamran M， et al.Hyperparameter Optimization of Bayesian Neural Network UsingBayesian Optimization and Intelligent Feature Engineering forLoad Forecasting. [ J]. Sensors ( Basel，Switzerland)，2022.22(12)：4446.

　　[20]常淼，沈艳霞.基于贝叶斯优化 CNN 的风电轴承故障诊断策略[J].噪声与振动控制，2021.41(06)：77-83.

　　[21] Domhan T，Springenberg J T，Hutter F.Speeding up automatichyperparameter optimization of deep neural networks by extrapolation of learning curves [ C ]//Proc of the 24thInternational Conference on Artificial Intelligence，2015 ：3460-3468.
 
 
关注SCI论文创作发表，寻求SCI论文修改润色、SCI论文代发表等服务支撑，请锁定SCI论文网！

文章出自SCI论文网转载请注明出处：https://www.lunwensci.com/ligonglunwen/56983.html