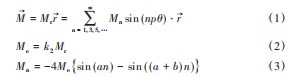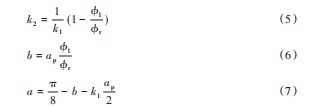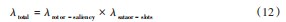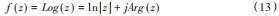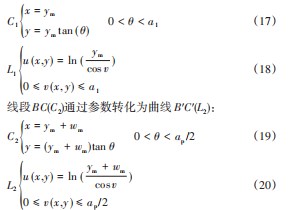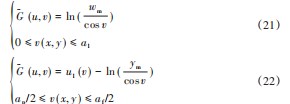SCI论文(www.lunwensci.com)
摘要:为了快速建立电机几何结构形状和电气参数与电机性能之间的关系,采用保角变换法,同时考虑定子开槽效应和转子凸极率,对内置式永磁同步电机空载气隙磁场进行了解析计算。影响电机性能的关键因素是气隙磁通密度的基波值和谐波含量,而改变磁极的几何参数会对气隙磁通密度的基波值与谐波含量产生影响,以气隙磁密谐波畸变率为目标函数,采用粒子群优化算法对转子永磁体的参数进行了优化。基于二维电磁有限元仿真分析,对一台8极48槽内置式永磁同步电机进行了有限元仿真,将解析计算结果与有限元法的仿真结果进行了对照,结果显示两者的波形吻合很好,验证了解析方法的准确性,为接下来的电机结构优化提供依据。通过粒子群优化算法改善了电机气隙磁密的正弦性,优化后减小了永磁同步电机的齿槽转矩,电机性能得到提高。
关键词:内置永磁电机;粒子群算法;保角变换法;气隙磁密;解析计算;齿槽转矩
Analytical Calculation of Magnetic Field of Interior Permanent Magnet Synchronous Motor Based on Conformal Transformation
Liu Xinggang,Yu Shenbo,Dou Rutong,Zhai Fengchen
(School of Mechanical Engineering,Shenyang University of Technology,Shenyang 110870,China)
Abstract:In order to quickly establish the relationship between motor structure shape,electrical parameters and motor performance,the no-load air gap magnetic field of interior permanent magnet synchronous motor(IPMSM)was analytically calculated by conformal transformation method,considering stator slotting effect and rotor saliency.The fundamental wave value and harmonic content of the air gap flux density are the key factors affecting the performance of the motor,and changing the geometric parameters of the magnetic poles will affect the fundamental wave value and harmonic content of the air gap flux density.Taking the harmonic distortion rate of the air gap flux density as the objective function,particle swarm optimization algorithm was used to optimize the parameters of the rotor permanent magnet.Based on two-dimensional electromagnetic finite element simulation analysis,48 slot of an 8 built-in permanent magnet synchronous motor had carried on the finite element simulation,the analytical calculation results with finite element method(FEM)simulation results of the comparison,the result showed that both the waveform match very well,verified the accuracy of the analytical method,provided the basis for structure optimization for motor.The sinusoidal characteristics of air gap flux density were improved by particle swarm optimization(PSO)algorithm,and the groove torque of PMSM was reduced after optimization,and the motor performance was improved.
Key words:IPMSM;PSO;conformal transformation;air gap flux density;analytical calculation;cogging torque
0引言
永磁同步电机由于具有结构简单、运行可靠、功率密度高的特点[1],因此被广泛应用于电动汽车、船舶等工业领域。内置式永磁电机与表贴式永磁电机相比优点是:永磁体位于转子内部,可以对永磁体起到很好的保护作用,其d轴和q轴的电抗不等,产生的磁阻转矩使永磁电动的输出能力得到提高[2]。
由于电磁场解析方法能够较好地揭示物理变化规律,这是其他方法所不能替代的[3],在电磁场理论发展中具有重要地位。常用的解析法分为等效磁网络法、基于矢量磁位的精确子域法与保角映射法等。等效磁网络法能够考虑气隙磁场中的各种漏磁磁阻,但模型搭建较为繁琐,计算量较大[4]。而基于矢量磁位的精确子域法,可以直接考虑定子槽对气隙磁场的影响,但随着边界条件的增加,求解变得较为困难[5]。保角变换是一种将复杂形状的多边形区域转换到规范面域的方法,从而将具有复杂边界条件的电磁场问题变得简单化,使用较为方便,故采用此种方法对内置永磁电机磁场进行解析计算。
一字型永磁体结构产生的径向磁密波形为矩形波[6],气隙磁通密度谐波含量较大。因此,本文以一台8极48槽永磁同步电机为例,通过对二维磁场的分析计算,采用粒子群优化算法对永磁体参数进行优化,以谐波畸变率为目标函数对电机进行优化,优化后电机齿槽转矩减小,为以后优化永磁同步电机噪声提供一定参考价值。
1解析模型
1.1内置永磁电机磁场
图1所示为8极48槽内置式永磁同步电机结构示意图,永磁体充磁方式为平行充磁。为了便于气隙磁场数值解析计算,需要对电机模型做出以下假设:(1)不考虑饱和效应(磁肋区除外);(2)定子槽简化为矩形形状;(3)气隙中的磁场分布由永磁铁产生的磁场与相对磁导率的乘积共同确定的;(4)永磁体产生的磁场是通过定子表面光滑的泊松方程二维解中获得的,即忽略定子开槽的影响。
在内置式永磁同步电机模型中,由于磁通通过转子铁心,使得磁通沿径向进入气隙场,而漏磁存在于磁阻区和磁肋区,如图2所示。漏磁效应被认为会降低永磁体的剩余磁通密度,磁化面积是恒定的[7]。
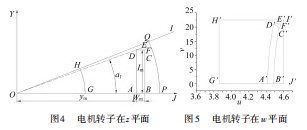
如图3所示,考虑边缘效应和漏磁效应的磁化强度
M,由傅里叶级数展开表示如下:
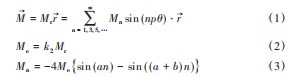
式中:Br为永磁体剩余磁通密度,假设磁路中的磁通密度完全饱和为Bs,是通过转子铁心的B-H曲线中获得的,可知等于2.0 T。
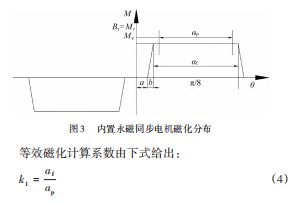
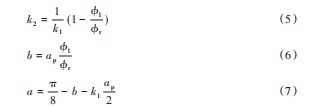
式中:ϕr=Br⋅S;ϕl=Bs⋅L⋅y;ϕr为通过永磁体的磁通量;ϕl为磁肋区域的漏磁通;S为永磁体面积。
磁场由等效磁化获得,气隙中磁通密度的径向分量由文献[7-8]中泊松方程获得。气隙通量密度分布如下:

1.2相对磁导率
对于内置永磁电机的磁场分析,应考虑转子凸极效应。由于内置电机转子中存在磁通屏障,沿转子圆周的磁通量会发生变化,因此应根据几何气隙函数确定和修改有效气隙长度(气隙函数)。为了考虑这种影响,通过引入转子凸极效应的相对磁导并乘以定子开槽电机的径向磁通密度计算电机磁场分布。
根据假设,气隙内的磁通密度分布表示为磁通量密度与相应相对磁导率的乘积。本文提出的分析方法的相对磁导率函数定义如下:
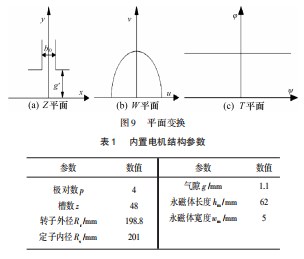
考虑定子开槽和转子凸极对气隙磁场的影响分别被定义为λrotor-saliency和λstator-slots,在本文采用保角变换的方法去考虑这俩个系数。保角变化法是将在平面内形状不规则的几何图形通过引入新的函数关系转换到另一个新的平面,使得转换后的几何图形在新平面上是规则,进而方便计算。如果假设原始电机配置放置在一个复杂的平面Z上,由振幅部分和角度部分组成。这个表达式满足柯西-黎曼方程,然后通过保形变换函数z=f(w),将其转换到新的平面W:
因此,在Z平面上的任意点坐标(x,y)通过公式转换成在W平面内点(u,v),其直角坐标分别由以下保角变换方程定义:

根据这个转换函数,原来在Z平面中1/16的转子区域被变换为W平面,图4所示为变换前的映射区域。通过使用对数函数,将原始z平面(图4)中提到的内置电机转子区域的1/16映射到w平面,如图5所示。原始区域和映射区域中每个区域的字母相同。
根据图4可知,曲线AD(C1)保角变换转化为直线A'D'(L1),通过以下参数表示:
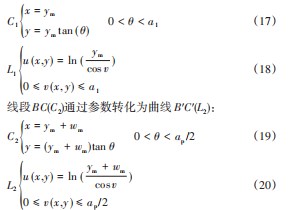
按照上述获得原始直线和曲线的变换曲线的过程,可以扩展作为变换定义域的段线AB、CD、CF、DE和EF,并使用上述映射,变换域的图像,其边界包括线段线、半线和曲线,如图4~5所示。对于每个区间v轴,u轴方向上曲线的总气隙长度定义为:
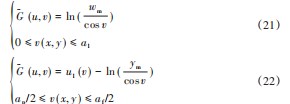
因此,根据上述电机不同内转子拓扑结构的曲线表示,气隙函数定义为:
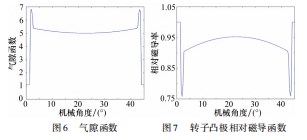
电机的气隙函数变化被确定并如图6所示。
在这里,新的气隙相对磁导函数,包括转子凸极的影响,忽略磁饱和漏磁通,大约等于:

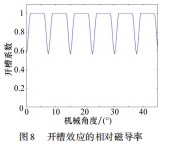
气隙的相对磁导函数由式(25)计算,如图7所示。
1.3定子开槽的影响
当对定子进行开槽时,磁通从气隙到定子铁心,气隙形状会发生变化,相对应的磁导率也会发生变化,进而对气隙中的径向磁通密度分布有很大的影响,并进一步影响了输出性能。在电机槽口范围内,气隙的形状发生变化进而相对磁导率小于1,而在定子齿中心线附近的一定范围内,气隙形状没有改变,相对磁导率为1保持不变。采用保角变换法对定子开槽后的气隙相对磁导率进行解析。由于此电机模型定子齿槽比较多,只能将定子槽假设为无限深。
并根据文献[9-10]使复平面Z内的气隙区域图形转变成W平面的图形,紧接着再通过函数变换,得到T平面所示的图形。即图8~9所示,实现定子开槽效应。
2磁场分布及有限元验证
为了验证解析方法的正确性,采用有限元软件对电机模型进行了仿真分析,并将解析计算和有限元仿真的结果进行了对比。以一台内置永磁同步电机为例,电机主要结构参数如表1所示。
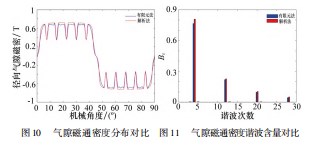
通过解析法与有限元分析法得到的空载气隙磁通密度径向分量波形对比如图10所示,此方法与有限元方法获得波形几乎相似。通过对其进行傅里叶分解,对应的谐波频谱如图11所示。解析法得出的图形比有限元方法略高,这是由于在解析过程中忽略了磁饱和效应和磁场边界条件导致的。
3粒子群算法寻优
粒子群优化算法源于对鸟群捕食的行为研究,粒子群优化算法(Particle Swarm OPtimization,PSO)是由Kennedy和Eberhart博士于1995提出的优化算法。其实质是一种智能化随机搜索算法,模拟鸟群觅食过程中的迁徙和群集行为。假设一群鸟在一片区域随机寻找食物,鸟群中的每只鸟在初始状态下是处于随机的位置且各个方向随机飞行但它们可以通过捕食经验和同伴发现获得相应的信息,进而调整飞行位置和搜索策略。即每个粒子通过统计迭代过程中自身的最优值和群体的最优值来不断修正自己的前进方向和速度大小,从而形成群体寻优的正反馈机制。PSO同遗传算法类似,是一种基于迭代的优化算法。系统初始化为一组随机解,通过迭代搜寻最优值。一经提出粒子群算法在函数优化、信号处理、机器人技术等领域得到了成功应用。粒子群优化算法不仅收敛速度快,且其程序实现简单需要调整的参数少实现容易[11]。内置式永磁同步电机,由于其结构特性,空载气隙磁密波形为矩形。为了使永磁电机气隙磁密波形具有良好的正弦性,采用粒子群优化算法以谐波畸变率为目标函数,并用k表示,对永磁体长度和宽度进行优化分析。因此新的结构尺寸应该是单目标、多变量、有约束的几何形状。其优化数学模型为:
式中:B 1为气隙磁密基波幅值;Bn为第n次气隙磁密谐波幅值。
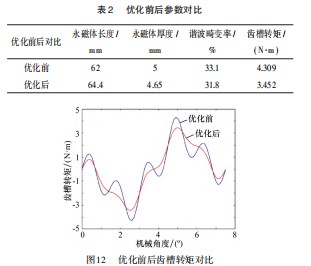
分别对优化前后的永磁电机进行有限元分析,优化前后参数对比如表2所示,优化前后齿槽转矩波形对比如图12所示,优化后齿槽转矩降低了19.8%。
4结束语
永磁同步电机的气隙磁场解析计算对于电机参数优化具有重要的意义。本文采用保角变换的方法对内置式永磁电机的磁场进行了计算,为了便于解析建模,对电机磁场的边界条件进行简化,将解析结果与有限元结果对比可以得出如下结论。
(1)采用保角变换法能够有效地对内置式永磁同步电机空载气隙磁场进行解析计算,其计算结果与有限元计算结果吻合很好,为电磁性能优化提供了参考,为接下来永磁同步电机优化提供依据。
(2)对磁场进行傅里叶分解,计算谐波畸变率,采用粒子群优化算法对电机谐波畸变率进行了优化,以永磁体参数作为优化变量,确定了最优永磁体结构尺寸,并通过有限元分析发现,新的结构尺寸可以有效减小永磁电机齿槽转矩,减少了19.8%。
参考文献:
[1]骆静,陈新华.基于多目标遗传算法的降低船用永磁电机齿槽转矩参数优化[J].科技视界,2021(21):136-138.
[2]吴帮超,黄开胜,赖文海,等.内置"一"型永磁同步电机齿槽转矩削弱[J].微特电机,2017,45(2):27-30.
[3]雷银照.关于电磁场解析方法的一些认识[J].电工技术学报,2016,31(19):11-25.
[4]Hemeida A,Lehikoinen A,Rasilo P,et al.A Simple and Effi⁃cient Quasi-3D Magnetic Equivalent Circuit for Surface Axial Flux Permanent Magnet Synchronous Machines[J].IEEE Trans⁃actions on Industrial Electronics,2018:1.
[5]Zhu Z Q,Wu L J,Xia Z P.An Accurate Subdomain Model for Magnetic Field Computation in Slotted Surface-Mounted Perma⁃nent-Magnet Machines[J].IEEE Transactions on Magnetics,2010,46(4):1100-1115.
[6]司萌,杨向宇,赵世伟,等.采用拼接式转子的内置永磁同步电动机的优化设计[J].电机与控制学报,2017,21(8):62-71.
[7]Kang,G H,H Jin.Analytical prediction and reduction of the cog⁃ging torque in interior permanent magnet motor[C]//IEEE Inter⁃national Conference on Electric Machines&Drives IEEE,2005.
[8]Zhu Z Q,Howe D.Instantaneous Magnetic Field Distribution in Brushless Permanent Magnet dc Motors,Part III:Effect of Stator Slotting[J].IEEE Transactions on Magnetics Mag,1993.
[9]Zhu,Z Q,Howe,et al.Analytical prediction of the cogging torque in radial-field permanent magnet brushless motors[J].Magnet⁃ics,IEEE Transactions on,1992,28(2):1371-1374.
[10]王兴华,励庆孚,王曙鸿.永磁无刷直流电机空载气隙磁场和绕组反电势的解析计算[J].中国电机工程学报,2003(3):126-130.
[11]林国汉,章兢,刘朝华,等.改进综合学习粒子群算法的PMSM参数辨识[J].电机与控制学报,2015(1):51-57.
关注SCI论文创作发表,寻求SCI论文修改润色、SCI论文代发表等服务支撑,请锁定SCI论文网!
文章出自SCI论文网转载请注明出处:https://www.lunwensci.com/ligonglunwen/51539.html