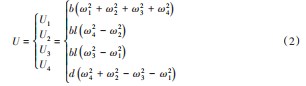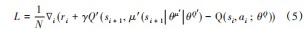SCI论文(www.lunwensci.com):
摘要:自主导航作为四旋翼无人机飞行导航的核心问题,为了更好地优化四旋翼无人机自主导航路径规划和路径跟踪能力,采用了一种基于改进的深度确定性策略梯度算法的机器学习算法(DDPG)的四旋翼无人机自主导航跟踪控制器,算法中增加了对动作探索策略的设计和对奖励函数的改进,以及采用二维及三维电子地图模拟四旋翼无人机的飞行轨迹,提出基于Matlab软件进行四旋翼无人机自主导航仿真实验以确保系统的稳定性和可行性。结果表明,所改进的深度确定性策略梯度算法可以在仿真实验中实现四旋翼无人机在二维及三维环境下的路径规划、跟踪与避障,并做到导航过程中的姿态状态的自主调整。
关键词:四旋翼无人机;强化学习;DDPG
Design and Research of the Quadrotor UAV Control System Based on Deep Deterministic Policy Gradient Algorithm
Kan Yaxiong1,Zhao Fei2
(1.Modern Equipment Manufacturing College,Zhenjiang College,Zhenjiang,Jiangsu 212028,China;2.College of Electrical and Information Technology,Zhenjiang College,Zhenjiang,Jiangsu 212028,China)
Abstract:Autonomous navigation is the core problem of four rotor UAV flight navigation.In order to better optimize the ability of four rotor UAV autonomous navigation path planning and path tracking,a four rotor UAV autonomous navigation and tracking controller were adopted based on improved depth deterministic strategy gradient algorithm(DDPG).In the algorithm,the design of action exploration strategy and the improvement of reward function were added,and the flight trajectory of four rotor UAV was simulated by two-dimensional and three-dimensional electronic map.It was proposed to carry out the autonomous navigation simulation experiment of four rotor UAV by using Matlab software to ensure the stability and feasibility of the system.The results show that the improved depth deterministic strategy gradient algorithm can realize the path planning,tracking and obstacle avoidance of four rotor UAV in two-dimensional and three-dimensional environment in the simulation experiment,and achieve the autonomous adjustment of attitude state in the navigation process.
Key words:Quadrotor UAV;reinforcement learning;DDPG
0引言
四旋翼无人机(Quadrotor UAV)作为一种复杂的无人技术设备,相对于常见的固定翼飞行器四旋翼无人机具有重量尺寸小、机动性能高和智能集成化程度高等优点,具备可以垂直起降在多种地形地貌地区,目前已经在军事、搜救、运输等行业得到了广泛的应用[1]。
目前国内外关于四旋翼无人机自主导航相关控制算法的研究如下:目前诸多研究者将深度学习与强化学习相结合,作为无人机器人系统的路径规划算法,得到了很大成就,使得无人机器人系统具备了面对复杂环境下快速反应快速变化导航策略的能力。王雷等[2]提出中小型无人机采用改进的自抗扰控制算法作为无人机自主飞行姿态解耦控制器的核心算法,计算机模拟实验证明了该算法在二维模拟仿真环境下具有可行性,在环境扰动干扰大小不确定或者环境干扰幅度较大情况下具有一定抗干扰优势。ZHOU L H等[3]提出采用串级PID算法作为四旋翼无人机二维轨迹姿态跟踪控制方法,控制系统的输入为期望的飞行二维轨迹和期望速度,通过串级PID算法输出四旋翼无人机的俯仰通道、滚转通道和偏航通道加速度的方法实现四旋翼无人机对复杂任务轨迹的轨迹跟踪。万惠、陈运剑等[4-5]讨论的DDPG算法具有多为特征提取功能,同时在未知环境下的依然可以保证避碰策略的准确性。张仕充、高敬鹏等[6-7]中优化了传统DDPG算法的训练速度,提高了算法中有关数据学习的效率。
基于上述文献启发,本文提出了一种基于改进的深度确定性策略梯度算法的四旋翼控制器设计方法,阐述了基于改进的深度确定性策略梯度算法的四旋翼无人机自主飞行控制器的整体框架,完善了算法中关于动作探索策略的设计并改进了与人工势场法相结合的奖励函数,最后在软件中模拟了四旋翼无人机自主导航仿真和位置跟踪仿真,实验中实现了四旋翼无人机在二维和三维环境下的自主导航路径规划、跟踪和避障功能。
1四旋翼无人机经典控制模型
根据相关资料[2],由经典Newton-Euler方程对四旋翼无人机建立六自由度的动力学模型为:
其中四旋翼无人机在空间中的位置坐标为(x,y,z);φ为滚转角;θ为俯仰角;ψ为偏航角;l为四旋翼无人机旋翼末端到质心的直线距离;m为四旋翼无人机负载总质量;Ii为转动惯量;U1、U2、U3、U4为计算得到的中间控制输入,定义为:
2四旋翼无人机控制器自主导航算法设计
2.1深度确定性策略梯度算法DDPG的基本流程
深度确定性策略梯度算法DDPG由深度神经网络和策略梯度算法DPG融合而成,并根据表演家-评论家算法提出了一个机器强化学习算法[8-9]。对于四旋翼控制器自主导航问题,主要目标是找到合适的自主导航算法以快速且稳定的方式将四旋翼从初始状态驱动到目标位置并悬停其上。在以上自主导航过程中需要自主导航算法不断连续处理高维数据,深度确定性策略梯度算法相较于传统智能算法可以处理高维且连续的动作,解决了其他智能算法只能处理低维度离散数据的不足。传统深度确定性策略梯度算法DDPG迭代步骤如下:
STEP1:算法将首先初始化表演家策略在线网络μ(s,θμ)和评论家评价网络Q(s,a;θQ),初始化参数θμ和θQ。初始化目标网络种的Q′:θQ‘←θQ和μ′:θμ‘←θμ,同时初始化经验池R。表演家策略在线网络根据策略模式选取一个动作at。其中行为策略根据当前在线策略网络μ和随机噪声N生成的随机过程,并从该随机过程进行采样获得动作值at=μ(st|θQ)+Nt。
STEP2:上一步中的输出动作at在被系统执行后返回奖励回报参数rt和下一个新的状态st+1。
STEP3:将系统状态量、输出动作、反馈奖励函数和下一步新的状态量(st,at,rt,st+1)储存在经验池R中,随后计算目标Q值targetQ=ri+γQ´(si+1,μ′(si+1|θμ)|θQ′)。通过损失函数的更新评论家网络的梯度,其中Q的损失函数使用均方差误差:
STEP4:更新在线价值网络Q及其参数θQ。更新目标网络使用随机梯度下降算法更新表演家策略在线网络参数θμ’,反复迭代计算更新评论家评价网络θQ‘。
如上述算法流程所示,深度确定性策略梯度算法DDPG在网络结构上和表演家-评论家算法基本相同,分为表演家网络和评论家网络。表演家网络的参数θμ可以理解为四旋翼无人机从位姿或位置状态到控制旋翼电机转速动作的映射。链式更新方式为:
式(4)中∇θμJ为策略梯度,评论家网络的参数为Q(si,ai;θQ),采用贝尔曼方程求解。此外,DDPG算法中通常还将平方差用损失函数L表示,损失函数L为:
式中:ri为构造回报参数;γ为折扣因子,最后式通过将L降低至最小的方式,更新评论家网络参数Q;表演家和评论家网络的更新版本分别为μ‘(s,θμ’)和Q‘(s,a;θQ‘)用于计算更新目标控制值。
2.2基于改进后DDPG算法的四旋翼无人机自主飞行控制器设计
图1所示为本文基于改进后DDPG算法的四旋翼无人机自主飞行控制器的整体框架图。由图1可知,控制器由两部分组成,其中四旋翼无人机的仿真环境包括无人机的实时状态量,包括无人机3个方向的轴加速度和角速度,以上状态量由仿真环境输入给策略网络。而四旋翼无人机的4个旋翼上电机的转速作为控制器反馈回无人机仿真环境的输出量或动作量以实时调节无人机的位姿及路径。
控制器另外一部分由两个策略网络构成,分别为控制器表演家网络和评论家网络。控制器的输入状态量(3个方向的轴加速度和角速度)为s0,输出(4个旋翼上电机的转速)为a0;四旋翼无人机的旋翼电机按照控制的输出转速a0动作后进入下一步s 1,并将动作a0送回给控制器评论家网络作为回报r0。然后控制器评论家网络根据四旋翼无人机返回下一步中的状态值s 1和奖励值r 1,更新旋翼电机的转速,并运用更新后的策略输出新的动作,重复上述过程直至四旋翼无人机最终达到控制目标。然后在传统DDPG算法的演算过程中,如果某些控制参数设计不当或控制器中的预期控制目标与系统实际状态之间误差过大会造成控制器策略网络模型的复杂程度急剧提高,导致过拟合或欠拟合的现象。为了解决深度确定性梯度策略算法中可能存在的过拟合问题,本文在传统DDPG算法的基础上做出了一些改进,包括如下设计。
(1)动作探索策略设计
传统DDPG算法中,系统在第一个状态s0时更新旋翼电机的转速a0后,送回初始奖励r0,控制器评论家网络获得送回后的奖励r0后,有一定概率会判断当前旋翼电机的转速执行动作足够好,而不去探索更匹配的转速执行策略来获得更大的r0′,使得系统无法达到需要的控制目标无法计算到全局最优解,只能计算到局部最优解。为了解决以上问题,可以借用ε−greedy(贪心算法)动作探索策略解决。四旋翼无人机以ε的概率选择一种旋翼电机的转速动作a,以1-ε的方式选择平均奖励最高的旋翼电机的转速动作r0′,以这样的方式得到概率最大的最佳旋翼电机的转速动作,通过完成最佳旋翼电机的转速动作四旋翼无人机就可以进入下个状态s 1。本文设计的动作探索策略为:
其中,N为噪声,是方差为σ的正态分布;kϵ[0,1)为ε−greedy算法中的衰减系数。
(2)与人工势场法相结合的奖励函数设计
当四旋翼无人机自主飞行控制器在状态s0下采取动作a0时,返回奖励函数r0的参数设计直接决定控制器的迭代计算时间和次数多少,并最终决定能否在迭代后最终求出全局最优解。神经元网络根据四旋翼无人机的状态值做出具体决策,环境根据送回的奖励值更新网络参数,使控制器评论家网络在下个状态s 1计算旋翼电机的转速时能够做出最匹配的决策。奖励函数设计如下:

式中:d(t)为四旋翼无人机当前时刻下距离控制目标终点的实时距离;d(t−1)为四旋翼无人机上一个时刻距离控制目标点的实时距离;do为四旋翼无人机是否碰撞到规划路径中障碍物的安全距离,当安全距离小于零时代表四旋翼无人机已经和障碍物发生碰撞,影响四旋翼无人机的飞行安全;dg为四旋翼无人机距离目标终点的阈值,小于该值即认为到达目标终点;dn为四旋翼无人机距离目标终点的距离,当四旋翼到达该范围内控制器将给予奖励+1,正向奖励可以促使四旋翼无人机更快到达目标终点。当机器人所处位置碰撞到障碍物时,控制器将给予奖励-100,负向奖励可以促使四旋翼无人机更快避开障碍物;当四旋翼无人机悬停时,则为-1的副奖励;其他情况则为-2作为负奖励,通过正负奖励的不同回报值来帮助四旋翼无人机最终靠近及到达目标点。
3仿真结果与分析
3.1四旋翼实验环境建模
为了验证基于改进的深度确定性策略梯度算法的可行性,仿真环境采用栅格法进行场景的二维及三维环境建模,在不同环境下进行了经典PID算法和改进后深度确定性策略算法的对比实验。表1所示为本文选用小型四旋翼无人机动力学模型相关参数。
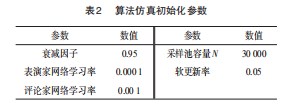
仿真实验在Windows系统下运行,系统采用Matlab2019b搭建四旋翼无人机的运动环境,该四旋翼无人机仿真使用M语言进行编程。实验分为简单二维栅格地图和三维地图。仿真中涉及的基于改进的深度确定性策略梯度DDPG算法仿真初始化参数如表2中所示。
3.2仿真实验结果
(1)二维环境仿真结果
如图2所示,本文采用Matlab2019b构建大小在100×100的二维栅格地图,栅格地图中包括大小不一的二维方块障碍物和圆形障碍物。目前地图中只存在静态障碍物,静态障碍物占总面积的20%~30%。图中起始点坐标为(0,0),黑色方格表示障碍物,其余为安全可飞行区域。目标点坐标为(100,100)。图2中红色实心路线和黑色虚线路线分别为四旋翼无人机在经典PID和改进的深度确定性策略梯度算法迭代200次后计算所获得的路径,可以看出经过改进的深度确定性策略梯度算法在避开障碍物前提下为从起点到目标点的最短路径。PID算法也可引导四旋翼无人机到达指定目标地,不过PID算法所规划路线与圆型障碍物发生碰撞,总体与改进的深度确定性策略梯度算法规划路线相比距离较长,且所规划路线在(75,40)和(70,70)等计算点上需要四旋翼无人机做出较大机动动作改变航向,不利于四旋翼无人机保持飞行姿态的稳定性。如图2~3所示,说明在二维仿真空间下,通过改进的深度确定性策略梯度算法不断迭代计算,可以让四旋翼无人机能够躲避二维空间中的不规则障碍物,并进行良好的路径规划和航迹跟踪。
(2)三维环境下仿真结果
如图4所示,本文采用Matlab2019b在三维环境下构建的仿真环境设置为20 m×5 m×6 m的区域,在空间中依次布置7个的长方体障碍物,这7个障碍物大小为1 m×4 m×5 m。在上述仿真环境下四旋翼无人机从起点(18,3,5)飞至终点(6,4,5)。基于改进的深度确定性策略梯度算法的四旋翼无人机控制器仿真目标是通过算法的不断迭代计算出最优自主导航路径,全程避开障碍物,到达目标点区域,由于三维场景复杂,传统PID算法已经无法有效规划导航路径,三维环境下仅采用改进的深度确定性策略梯度算法测试算法有效性。
仿真实验开始后,改进的深度确定性策略梯度算法控制器的三维空间位置自主导航结果如图5~6所示。由图可以看出基于改进的深度确定性策略梯度算法控制器计算出最优导航路径相较于起点到终点的理想路径而言,路线更加平滑稳定且对三维障碍物依旧有着良好的避障效果。跟踪过程中,四旋翼无人机在X、Y、Z轴上的距离误差不超过±0.5 m。
综合考虑后可以得出结论:二维环境仿真下,改进的深度确定性策略梯度算法相较于传统PID算法提高了四旋翼的自主导航规划路线能力,三维环境仿真下改进的深度确定性策略梯度算法可以有效地实现较复杂三维真实飞行环境的自主导航和障碍物避障。
4结束语
本文针对四旋翼无人机设计了一种改进的深度确定性策略梯度算法,通过设计新的动作探索策略并利用人工势场法选择更加有效的最优动作,保证了四旋翼无人机快速准确识别最优行动方向。仿真四旋翼无人机在二维和三维空间内被障碍物所阻挡从而降低自主飞行效率。仿真实验对比了传统PID算法和改进的深度确定性策略梯度算法,结果表明改进的深度确定性策略梯度算法提高了四旋翼的自主导航规划路线能力。后续将进一步开展所设计算法的改进工作,继续提高系统的响应时间和鲁棒性。
参考文献:
[1]王玉山,王伟,王智琪.地空两用农业信息采集机器人设计[J].机电工程技术,2017,46(11):67-70.
[2]王雷,石鑫.基于改进蚁群算法的移动机器人动态路径规划[J].南京理工大学学报,2019,43(6):700-707.
[3]ZHOU L H,ZHANG J Q,DOU J X,et al.A fuzzyadaptive back⁃stepping control based on mass observer fortrajectory tracking of a quadrotor UAV[J].InternationalJournal of Adaptive Control and Signal Processing,2018,32(12):1675-1693.
[4]万惠,齐晓慧,李杰.基于SADRC的四旋翼姿态解耦控制及稳定性分析[J].北京大学航空航天大学学报,2020(12):2274-2283.
[5]陈运剑,刘畅,马武举,等.基于非线性制导的四旋翼轨迹跟踪控制[J].计算机测量与控制,2020,28(1):101-105.
[6]张仕充,时宏伟.基于DDPG的飞行器智能避障仿真应用研究[J].现代计算机,2021(5):80-85.
[7]高敬鹏,胡欣瑜,江志烨.改进DDPG无人机航迹规划算法[J].计算机工程与应用,2021,66(3):1973-1983.
[8]李众,沈炜皓.四旋翼飞行器姿态跟踪的RBF-PD方法研究[J].计算机应用研究,2021(1):164-180.
[9]孟晨阳,郝崇清,李冉,等.基于改进DDPG算法的复杂环境下AGV路径规划方法研究[J].计算机应用研究,2021(39):57-63.
[10]TSITSIKLIS J N,VAN R B.An analysis of temporal-difference learning with function approximation[J].IEEE Transactions on Automatic Control,1997,42(5):674-690.
[11]MNIHV,KAVUKCUOGLUK,SILVER D,et al.Playing atari with deep reinforcement learning[C]//Proceedings of Workshops at the 26th Neural Information Processing Systems 2013.Lake Ta⁃hoe,USA,2013.
[12]萨顿理查德,巴图·安德鲁.强化学习[M].2版.北京:电子工业出版社,2019.
关注SCI论文创作发表,寻求SCI论文修改润色、SCI论文代发表等服务支撑,请锁定SCI论文网!
文章出自SCI论文网转载请注明出处:https://www.lunwensci.com/ligonglunwen/49860.html