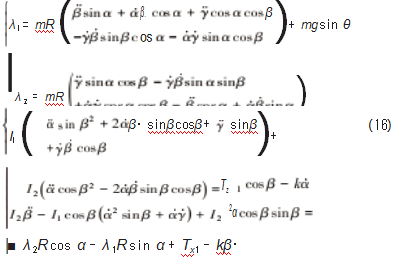磁驱动双半球胶囊机器人爬坡运动分析论文

 

SCI论文（www.lunwensci.com）：
 

　　摘要： 胃及肠道内表面布满环形皱襞，  凹凸的复杂作业环境给磁驱动双半球胶囊机器人姿态能否稳定回归带来不确定性，  且肠道 起伏的表面迫使机器人应具备一定角度的爬坡行走能力。基于空间旋转磁场与机器人的随动效应，  采用拉格朗日乘子法建立主动 模态下爬坡滚动的完整动力学模型，  通过姿态角仿真分析验证了模型的正确性。为进一步分析机器人的爬坡能力，  建立简化动力 学模型，  结合由动量矩定理推导的纯滚动条件，  仿真相关参数与纯滚动爬坡角度关系。仿真表明：  机器人爬坡时姿态具备一定的 抗干扰能力，  且在规定范围内，  增大磁场强度和摩擦因数，  可以增强机器人的爬坡能力。上述结论为延展胶囊机器人的作业场合 提供了理论支持。

　　关键词：双半球胶囊机器人；  爬坡动力学模型；  爬坡性能；  滚动行走
 

Analysis of Climbing Motion of a Dual Hemispherical Capsule Robot Actuated by Rotating Magnetic Field

Chen Ziqiang，  Zhang Yongshun
(Key Laboratory for Precision & Non-traditional Machining of Ministry of Education, Dalian University of Technology,
Dalian, Liaoning 116024, China)

　　Abstract: The inner surface of the stomach and intestine is covered with annular folds . The complex working environment brings uncertainty to the stable return of the posture of the magnetic driven double hemisphere capsule robot, and the undulating surface of the intestine forces the robot to have the ability of climbing at a certain angle. Based on the follow-up effect of the robot, a complete dynamic model of climbing and rolling was established by using Lagrange multiplier method. The correctness of the model was verified by attitude angle simulation analysis . In order to further analyze the climbing ability, a simplified dynamic model was established. Combined with the pure rolling condition derived from the momentum moment theorem, the relationship between relevant parameters and pure rolling climbing angle was simulated . The simulation shows that the attitude of the robot has certain anti-interference ability, and the climbing ability of the robot can be enhanced by increasing the magnetic field strength and friction coefficient within the specified range . The above conclusions provide theoretical support for the operation of extended capsule robot.

　　Key words:  dual hemisphere capsule robot; climbing dynamics model; climbing performance; rolling locomotion

　　0    引言

　　胶囊内窥镜相较传统胃镜具有诊断无痛、安全的优点，  被 广泛应用在胃肠道疾病检查中。虽然目前以 Given ImagingLtd 的 M2A 和金山科技初代的 OMOM 为代表的国内外胶囊机器人 已技术成熟且投入商用，  但它们大多数依靠胃肠道蠕动行进， 位姿随意性强，  漏检率高[1]。因此开发可灵活行走且姿态可控 的主动式胶囊内窥镜便尤为重要。

　　目前主动式胶囊机器人驱动方式主要分为执行机构驱动 和永磁体驱动，  前者结构复杂，  不利于胶囊微型化的同时也 存在电源模块工作时长受限的问题，  后者则由于受制梯度磁 场而较难实现胶囊位置与姿态的分离控制。本课题组利用已 有的三轴亥姆霍兹线圈装置产生的空间均匀万向旋转磁场与 胶囊内嵌永磁体耦合生成的磁力矩驱动整体实现自旋与前进 后退 [2-4]。随动效应[5] 使机器人轴线可以时刻跟随磁矢量法线方向，  借此实现胶囊被动模态的悬停调姿和主动模态的滚动 行走，  控制更加灵活。

　　常规球形机器人依靠摆锤或配重块等改变重心来驱使整球 滚动，  其平面滚动速度和爬坡能力受制于偏心装置的质量占 比，  爬坡效果不理想[6]。将耦合磁力矩作为驱动源，  本文中的 机器人具备更好的爬坡效果。

　　为使采集的图像稳定可用，  胶囊机器人爬坡时需有良好的 抗干扰能力。描述机器人位姿的状态变量互不独立，  是典型的 非完整性约束系统，  动力学建模工作更加复杂。

　　本文采用拉格朗日乘子法建立描述机器人爬坡的完整动 力学模型，  分析与姿态角相关的夹角变化，  说明了机器人 的 抗 干 扰 能 力 。建 立 简 化 爬 坡 动 力 学 模 型 分 析 爬 坡 角 度 。 理论分析和试验结果为改善和提高机器人爬坡性能提供了 理论支持。

　　1   机器人结构

　　如图 1 所示，  内置轴承实现主动半球壳体和被动半球壳体 的悬浮连接，  保证两半球间的相对转动。  NeFeB 永磁体与主动 半球壳固连，  当外部磁场旋转时，  受到磁力矩驱动的永磁体带 动主动半球一同旋转，  与摄像头定位器件等固连的被动半球因 无动力而不旋转。为实现图像采集等功能，  零件还包括发射天 线、  LED 电路、摄像头、电池、电路板等。当机器人轴线因随 动效应而随磁场轴线变为水平方向时，  与肠道接触的主动半球 将借助摩擦力带动整球一同滚动 [7]。
 

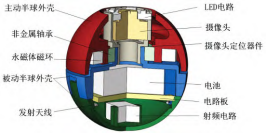
图 1    双半球胶囊机器人结构

　　2   爬坡完整动力学建模与动态特性分析

　　2.1   建立坐标系

　　机器人涉及姿态变化的爬坡过程如图 2 所示。
 

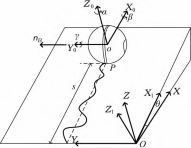
图 2    爬坡运动示意图

　　各坐标系情况如图 3 所示。

　　( 1 )   如图 3  (a)  所示，  OXYZ 为惯性坐标系，  OX 轴与水 平面重合。旋转磁矢量 B绕原点 O 在 XOZ 面内旋转，  磁矢量法 线 nB 方向与 OY轴平行。

　　( 2 )  OX1 Y1Z1 为固定坐标系，  OX1 轴与水平面夹角为 θ。(x, y)  为机器人球心 o 在 OX1 Y1Z1 内的坐标。

　　( 3 )  ox0y0z0 为平动坐标系，  坐标系原点 o 与球心重合。

　　( 4 )  oxyz 为描述机器人位姿的赖柴坐标系。如图 3  (b)， 先绕 oz0 轴旋转 α 角得到中间坐标系 oxy1z0，  再绕 ox 轴旋转 β 角 得到赖柴坐标系。机器人的轴线 n 最终与 oy 轴重合。

　　( 5 )  ox1yz1 为机器人本体坐标系。由坐标系 oxyz 绕 y 轴旋转 γ 角得到。

　　为描述机器人爬坡时包含姿态变化的完整动力学方程，  有 广义坐标：  坐标 x 、y，  姿态角 α 、β 及 γ。设机器人半径为 R， 质量为 m，  机器人和坡面的接触点为 P，   内嵌永磁体磁矩为 m0，  旋转磁矢量强度幅值为 B0。
 

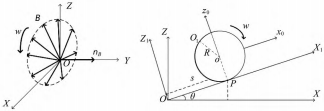
(a)  惯性坐标系

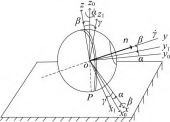
(b)  赖柴坐标系
图 3    各坐标系示意图　

　　2.2    非完整性约束方程

　　假设机器人爬坡全过程为纯滚动[8]。角速度经一系列坐标 变换后，  在坐标系 ox0y0z0 中可表示为：

　　　（１）

　　在坐标系 ox0y0z0 中，  矢量 oP 表示为：

　　oP = [ 0   0    -R ]T　　　　（２）

　　纯滚动时，  速度瞬心点 P 的速度表达式为： VP  = Vo  + ω 0  × oP = 0　（３）

　　于是点 o速度为：

　　　（４）

　　将式  (1)  代入式  (4)，  得非完整约束方程：

　　　　（５）

　　2.3   磁力矩与阻力矩计算

　　如图 3  (a)  所示，  磁矢量 B 的旋转速度为 ω，  在惯性坐标 系 OXYZ 中的表达式为：
　　
　　B = [ B0 sin ωt   0   B0 cos ωt ]T　　（６）

　　则经过坐标转换，  B 在赖柴系 oxyz 中为：

　　B 1  =          　（７）
       

　　其中：

　　A = sin α cos β cos θ + sin θ sin β

　　B = sin β cos θ - sin α cos β sin θ

　　C = sin α sin β cos θ - sin θ cos β

　　D = sin α sin β sin θ + cos β cos θ

　　和机器人固连的永磁体磁矩 m 在 oxyz 中表示为：

　　

　　式中：  ε 为转差角，   即机器人旋转时磁矩矢量滞后磁矢量的 角度。

　　参考磁力矩公式 T1=m1×B1，  得到 T1 在赖柴系 oxyz 中的分量 表达式：

　　        ( 9 )

　　其中  ：    E = B0 cos α cos θ sin ωt + B0 cos α cos ωt sin θ, F = B0 cos ωt (cosβ cos θ + sin α sinβ sin θ)。
　
　　爬坡时，  阻力矩包括机器人壳体与肠道相对滑动受到的粘性 摩擦力矩，  以及静摩擦力所产生的摩擦阻力矩。设粘性阻尼系数为k，  静摩擦力为mgsinθ，  则阻力矩Mf在赖柴系oxyz中可表示为：

　　Mf  = -kα.k0 - kβ.i - mgR sin θj                                        ( 10 )

　　式中：  k0 、i 、j 分别为z0 、x 、y 轴的单位向量。

　　2.4  爬坡完整动力学方程

　　非完整约束使得广义坐标之间失去独立性，  拉格朗日乘子法可以很好解决此问题，  其表达式为：

　　 - = Q α  +λ r  α = 1, 2, …, u            ( 11 )

　　式中：  L 为拉格朗日函数；  qα为广义坐标；  Qα为广义力；  λr为 拉格朗日乘子；fr 为非完整约束方程。

　　经变换，  oxyz 中机器人角速度 ω1 表示为：

　　                                         ( 12 )

　　设 T为系统动能，  其包括平动动能和转动动能，  联立式  ( 5 )( 12)  有：

　　T = m (x.2 + y.2) + I2 ωx 1 2 + I1 ωy1 2 +  I2 ωz 1 2

  　　 =m (x.2 + y.2) +  I2 β.2 +  I1 (γ. + α. sinβ)2 +  I2 ( α. cosβ)2  ( 13 )

 

　　式中：  I1 为极转动惯量；  I2 为赤道转动惯量。

　　取水平面为零势能面，  则势能 V 为：
　
　　V = mg (s sin θ + R cos θ)     ( 14 )

　　式中：  s 为球心位移在 OX1方向的投影，  即 x。

　　拉格朗日函数 L=T-V，  其表达式为：

　　L =  m (x.2 + y.2) + I2 β.2 +  I1 (γ. + α. sinβ)2 + I2 ( α. cosβ)2 - mg (x sin θ + R cos θ)   ( 15 )

　　则机器人主动模态下的爬坡完整动力学方程为：

　　

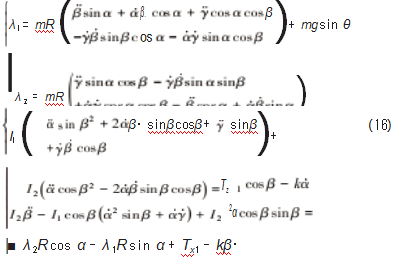
　　为了方便分析机器人的姿态角响应特性，  取状态变量 x= ( α，  β，  α., β.)  T。当机器人爬坡滚动不丢步时，  可将自转角 γ 替换为 ωt-ε，  于是可得到 x. =f (x,t) ⋅ x 形式的方程组：

　　

　　其中：

　　M = B0 cos ωt (sinβ cos θ - sin α cosβ sin θ)-B0 sin ωt (sin α cosβ cos θ + sin θ sinβ)

　　N = kα. + 2I1 α.β. sinβ cosβ + I1 β.ω cosβ - 2I2 α.β. sinβ cosβ

　　P = I1 sinβ cosβα.2 + I1 ωα. cosβ - I2 α.2 sinβ cosβ 

　　Q = Rα.β. cos α - Rβ.ω sinβ cos α - Rα.ω sin α cosβ  

　　Z = -Rβ.ω sin α sinβ + Rα.ω cos α cosβ + Rβ.α. sin α

　　Y = B0 cos ωt (sinβ cos θ - sin α cosβ sin θ)-B0 sin ωt (sin α cosβ cos θ + sinβ sin θ)

　　式  (17)  即为可以描述姿态角变化的微分方程组。

　　2.5  爬坡动态特性分析

　　将旋转磁矢量所属平面的法线 nB    (磁场轴线)  调整为水平 时，  借助随动效应，  机器人的轴线 n 可以近乎时刻与 nB 重合， 进而以主动模态完成爬坡运动。然而胃肠道空间并不宽裕，  机 器人在行进时难免受到胃肠壁刮蹭等环境干扰。将 n 与 nB 间的 夹角 σ 作为反映机器人轴线偏离目标方位的目标函数，  其与姿 态角 α、β 之间的数学关系为：

　　σ = arccos()= arccos(cos α cosβ)      ( 18 )

　　给定初值不同的 σ来模拟实际作业时受到的环境干扰，  结合式  (17)  线性化后的微分方程组分析机器人轴线姿态回归的 能力。具体仿真参数如表 1。

　　从图 4 中可以看到，  在 90°极限范围内，  无论初值 σ选取多大，  经一段时间后都能收敛于 0°，  且 σ的初值越小，  其回归的也越快。这表明受到干扰时，  机器人具备回归稳态的能力， 这为机器人的多场景稳定行走提供了理论支持。
 

表 1     仿真参数取值

 

 

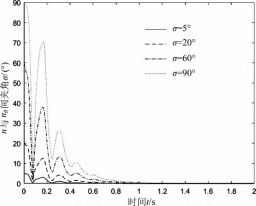
图 4    不同初值时 σ 的时间响应曲线

　　3   爬坡运动平面动力学建模与爬坡能力分析

　　3.1    前向爬坡动力学建模

　　为了方便探究机器人的爬坡能力，  可以建立不含姿态角的 坡面运动动力学方程。如图 5 所示，  建立坐标系OX2 Y2。
 

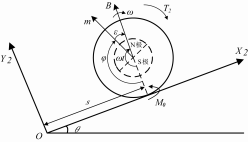
图 5    球形机器人爬坡运动简化模型

　　取爬坡位移 s 为广义坐标，  滚动摩阻为 M0，  机器人绕转轴 的转动惯量为 I1，  滚过角度为 φ。故有关系：

　　s. = Rφ.                                                                              ( 19 )

　　考虑到轴承间粘性阻尼不可忽略，  采用基于能量耗散的拉 格朗日方程，  形式如下：

　　()- = Qj  -      j = 1, 2, …, u 1  （20）
 

　　系统动能 Ta 为：

　　Ta  = ms.2  + I1 ()2  （21）
 

　　取水平面为零势能面，  则任意位置的势能 Va 为：

　　Va  = mgR ( sin θ + cos θ)  （22）
 

　　耗散函数 ψ：

　　ψ =  k 1 ()2  （23）

　　式中：  k1 为轴承间的粘性摩擦因数。

　　机器人受到的主动力包括：  耦合磁力矩 T2、重力 mg 以及滚动摩阻 M0。根据虚功原理，  广义力可表示为：

　　Q = T2 /R - mg sin θ - M0 /R =m0 B0 sin (ωt - )/R - mg sin θ -  σ 0 mg cos θ sgn ()/R  ( 24 )
 

　　式中：  σ0 为滚动摩阻系数；  引入符号函数 sgn，   旨在滚动摩阻 方向时刻与角速度方向相反。最终可得到平面动力学方程：

　　(m +)  + mg sin θ = m0 B0 sin (ωt - )/R - mg sin θ - σ 0 mg cos θ sgn ()/R -  s.  ( 25 )

　　3.2    纯滚动条件分析
 

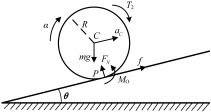
图 6    胶囊机器人斜面纯滚动时的受力模型

　　假设机器人向右滚动，  角加速度为 α，  质心 C 的加速度为 aC，  静摩擦力为f，  静摩擦因数为fs。根据动量矩定理可得[9]：

　　maCx  = f - mg sin θ
　　maCy  = FN  - mg cos θ                                                    ( 26 )
　　Iα = T2  - fR - Mo

　　式中：  滚动摩阻 M0=σ0mgcosθ；  因为 aCy=0，  故 aCx=aC；  点 P 为 速度瞬心，  故有 aC=αR。

　　纯滚动时满足：  f ≤ fsFN，  也即f ≤ fsmgcosθ。结合上述条 件，  可得纯滚动条件为：

　　

　　3.3  爬坡能力仿真

　　固定参数 ω =12π rad/s，  I1=1.78×10-7 kg ·m2，  取磁场强度 B0 的仿真上限为 12 mT[10-11]，  利用 Matlab 对式  (25)  进行仿真， 得到图 7所示关系曲线。
 

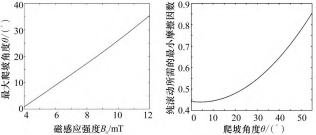
图 7  爬坡角度和磁场强度关系曲线   图 8  最小静摩擦因数与角度关系曲线

　　可以看到，  随着磁场强度 B0 的增大，  机器人的最大爬坡角 度也变大，  爬坡能力增强。

　　保持磁场强度 B0=8 mT，  结合式  (28)，  仿真得到各个爬坡 角度下纯滚动时所需的最小静摩擦因数曲线。由图 8可知，  爬 坡角度越大，  纯滚动时所需的静摩擦因数越大。当肠道环境达 不到对应爬坡角度所需的最小静摩擦因数时，  机器人便发生打 滑甚至空转。

　　为更好地说明纯滚动转变为滑动的条件，  保持 B0 分别为 8 mT、9 mT、11 mT，  仿真得到图 9。人体肠道的静摩擦因数fs 为 0.6左右[12]，  故以 0.6作为对照值。当 B0=8 mT 时，   由图 7 可 知，  此时机器人的爬坡角度为 17°，  在图 9 中找到 17°时保证 纯滚动的最小静摩擦因数fs min=0.47，  小于 0.6，  因此机器人可 以按设定速度爬坡。同理，  B0=9 mT对应的坡角为 21.5°，  参照 图 9，  此时满足纯滚动所需的fs min=0.54，  同样小于肠道可以提 供的最大静摩擦因数。当 B0=11 mT 时，  爬坡角度为 30°，  此时 纯滚动所需的fs min=0.725，  大于肠道所能提供的最大静摩擦因 数，  因此机器人将发生打滑甚至空转。
 

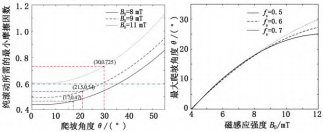
图 9  不同B0对应的爬坡角度与摩擦因数的关系曲线 图 10 典型静摩擦因数下最大爬坡角度曲线
 

　　结合纯滚动要素，  绘制不同静摩擦因数下机器人纯滚动的 最大爬坡角度与磁场强度关系曲线。从图 10 可知，  在几种典 型肠道静摩擦因数中，  静摩擦因数越大，  机器人的爬坡极限值 越大，  爬坡表现越好。

　　4  结束语

　　本文的创新点在于根据拉格朗日乘子法建立了磁驱动胶囊 机器人主动模态爬坡时的完整动力学方程，  通过仿真机器人轴 线回归预设方位情况说明了机器人的抗干扰能力；  根据基于能 量耗散的拉格朗日动力学原理建立二维爬坡动力学模型，  结合 纯滚动条件仿真磁场强度与肠道静摩擦系数对于爬坡能力的影 响规律。

　　仿真结果表明：  机器人爬坡时具备良好的姿态回归能力， 其抗干扰特性为保证机器人爬坡的顺利行走及稳定图像采集功 能奠定了基础；  在一定范围内，  磁场强度越大，  机器人的爬坡 表现越好，  大的肠道静摩擦因数将增大机器人的最大不打滑爬 坡角度，  这一结论对于改善机器人在大坡度时的打滑问题提供 了解决思路，  对于未来越障方面的研究也具有参考价值。

　　参考文献：

　　[1] 颜国正, 陈雯雯 . 肠道内窥镜机器人研究进展[J]. 生物医学工 程学杂志, 2015, 32(1): 214-217.

　　[2] ZHANG Y S, WANG N, DU C, et al. Control theorem of a univer⁃ sal uniform-rotating magnetic vector for cap-sule robot in curved environment[J]. Science China Technological Sciences, 2012, 56(2): 359-368.

　　[3] Zhang Y, Chi M, Su Z. Critical Coupling Magnetic Mo-ment of a Petal-Shaped Capsule Robot[J]. IEEE Trans-actions on Magnet⁃ ics, 2016, 52(1):1-9.

　　[4] Zhang Y S, Yu Z C, Yang H Y, et al. Orthogonal transformation operation theorem of a spatial universal uniform rotating magnet⁃ ic field and its application in cap-sule endoscopy[J]. Science China, 2017, 60(6): 1-11.

　　[5] 张永顺 , 王楠 , 马壮 . 肠道胶囊机器人的转向随动力学模型 [J]. 机械工程学报, 2012, 48(1): 84-90.

　　[6] RANJAN M, MARK A M, JAY T P. Motion planning for a spheri⁃ cal mobile robot: Revisiting the classical ball-plate problem [J]. Transactions of the ASME, 2002(124): 502-511.

　　[7] 张永顺, 周华涛, 张林霞, 等 . 一种新型双半球形胶囊机器人 [J]. 机械工程学报, 2017, 53(15): 110-118.

　　[8] Zhan Q, Cai Y, Liu Z. Near-Optimal Trajectory Planning of a Spherical Mobile Robot for Environment Exploration[C]//2008 IEEE Conference on Robotics, Automation and Mechatronics, September 21-24 2008, Chengdu, China. New York: IEEE, 2008: 84-89.

　　[9] 姜芳 , 赵东 . 纯滚动圆轮静摩擦力方向的确定[J]. 力学与实 践, 2011, 33(1): 86-88.

　　[10] 纪璇 . 双半球胶囊机器人滚动动态性能研究[D]. 大连:大连 理工大学, 2021.

　　[11] 高晋阳 . 用于肠道诊查的微型仿生机器人关键技术研究 [D]. 上海:上海交通大学, 2017.

　　[12] 汪炜 . 胃肠道无创诊查微型机器人系统设计与优化[D]. 上 海:上海交通大学, 2020.