SCI论文(www.lunwensci.com):
摘要:剩余寿命预测在提高机械设备轴承的可用性和生产率方面发挥着重要作用。为了提高轴承运行过程中实时剩余寿命预测的准确性,提出了一种轴承核密度估计的剩余寿命预测方法,利用部件连续退化的特征量构建退化分布的核密度估计模型,然后得到剩余寿命的概率分布函数。随着监测数据的实时变化,利用已知样本的核密度估计来递归更新新样本的核密度估计,然后更新预测模型。轴承磨损试验表明,该模型能够准确预测轴承的剩余寿命,与维纳过程的预测模型相比,验证了核密度估计模型在剩余寿命预测中的准确性。
关键词:核密度估计;自适应窗宽;局部窗宽因子;剩余寿命预测
Remaining Useful Life Prediction Based on Adaptive Kernel Density Estimation
Wu Chongfeng
(Jineng Holding Yangquan Guzhuang Coal Industry Co.,Ltd.,Yangquan,Shanxi 045060,China)
Abstract:Remaining life prediction plays an important role in improving the availability and productivity of bearings in machinery and equipment.In order to improve the accuracy of real-time remaining life prediction during bearing operation,a bearing kernel density estimation method for remaining life prediction was proposed.The characteristic quantities of continuous component degradation was used to construct a kernel density estimation model of the degradation distribution,and then the probability distribution function of the remaining life was obtained.As the monitoring data changes in real time,the kernel density estimates of known samples were used to recursively update the kernel density estimates of new samples,and then the prediction model was updated.Bearing wear tests show that the model is able to accurately predict the remaining life of the bearing,validating the accuracy of the kernel density estimation model in remaining life prediction when compared to the prediction model of the wiener process.
Key words:kernel density estimation;adaptive window width;local window width factor;remaining useful life prediction
0引言
随着机械设备不断向智能化和精密化方向发展,轴承作为机械设备的关键部件,其性能退化直接影响整个设备的性能[1-4]。为此,对轴承进行实时监测和剩余寿命预测有着十分重要的研究价值和意义。现研究阶段可将剩余寿命预测的方法大致分为基于物理失效模型、基于知识表示和数据驱动的方法[5]。面对复杂的设备,获得物理模型是很困难的,知识表示方法更适合定性推理,不太适合定量计算,而且很难获得完整的知识。然而,数据驱动的预测方法,通过对轴承性能数据的描述,提取有用的信息并预测剩余寿命[6]。Si等[7]将数据驱动方法的伽马分布、回归模型、Wiener过程和随机滤波模型[8]等RUL模型进行总结分析。Pei等[9]提出双时间尺度的随机退化设备的非线性退化模型。Zhai等[10]提出基于高阶隐半马尔科夫模型的剩余寿命预测模型。上述数据驱动的方法大多需要假设退化模型和参数估计,而参数估计方法在模型选择上存在局限性,过分依赖概率密度函数形式的先验定义,因此不能保证预测模型的准确性和适用性。
本文提出一种轴承核密度估计的非参数剩余寿命预测模型,该方法不对数据分布附加任何假设,而是从数据本身研究数据分布的特点,避免了大多数数据驱动方法需要模型假设和参数估计的问题。该模型在核估计窗宽的选取上引入局部窗宽因子构建自适应窗宽模型。模型通过计算样本点的密度来自适应选择样本点窗宽,提高了核密度估计窗宽选择的可靠性,从而提高了预测精度。最后通过轴承磨损试验验证了所提模型的适应性和准确性。
1核密度估计模型的构建
核密度估计方法不利用数据分布的先验知识,不对数据分布进行假设,它是一种用于从数据本身估计未知变量的概率密度函数的方法[11-12]。其由已知的N个样本点,通过选择任意核函数及窗宽得到N个核函数,通过线性叠加得到核密度的估计函数。设Δx 1,Δx2,⋯,Δxn为n个独立且同分布的退化样本,f(Δx)为其服从十五概率密度函数,则核密度估计的概率密度函数f者(Δx)表示为:
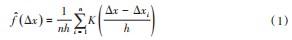
式中:h为窗宽;K(·)为核函数;n为样本数。
其中,K(·)和h选用的恰当与否决定了核估计的准确度高低。核函数作为影响核密度估计的一个因素,一般情况下任何函数都可作为核函数,常用的有四次核、均匀核、三角核和高斯核。核函数的选择虽多,但对核密度估计的准确度作用不大。本文选用广泛应用的高斯核函数。即:
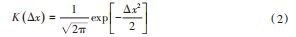
窗宽h作为影响核密度估计平滑性和核函数宽度的主要因素,当h较小时,核密度估计曲线不平滑且曲折,揭示了更多细节;当h较大时,核密度估计曲线平滑,但会覆盖更多的细节。因此,选择合适的窗宽对核密度估计是非常重要的。
2自适应窗宽模型建立
目前自适应窗宽是窗宽选择的主流方向,其本质是随着样本点的增加能够自适应的选取窗宽,减少了计算量。在现有研究阶段常用的自适应窗宽方法大多采用的是通过式(3)积分均方误差求其最小值得到初始最优窗宽hn。
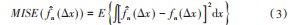
核密度估计模型中的初始最优窗宽hn,通过式(3)积分均方误差求其最小值点minMISE(f者h)得到:
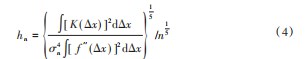
将高斯核函数代入式(4)可求出hn为:
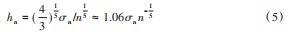
式中:σn为n个初始样本特征退化增量的方差。
该窗宽方法解决了样本数据实时变化时选择窗宽和实际中固定窗宽造成的过度(不足)拟合问题。如果样本分布是近似正态的,这种方法是最佳选择。然而,当样本分布不对称或有多个峰值时,该方法会导致过度平滑,精度需要提高。
然而,在实时监测轴承的核密度估计过程中,为了提高窗宽对真实样本数据分布的适应性,引入了一个反映基于最优窗宽hn的样本点分散度的函数λi来自适应选择窗宽。λi可通过式(6)各个样本点处的概率密度得到:

将函数λi与式(5)计算出窗宽hn相乘可得自适应窗宽hi:
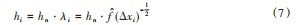
从而使得不同样本的窗宽可以根据样本数据的稀疏程度进行自适应调整,以更好地满足实践中核密度估计的需要。
因此,将自适应窗宽h(Δxi)方法引入核密度估计的模型中,从而构建自适应核密度估计的表达式为:
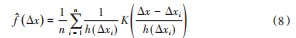
由于在实际应用中样本数据都是实时更新的,如果每增加一个样本都对其从头开始计算,那么计算量会随数据的增多变得复杂化。所以,为使核估计的计算性能得到提升,通过用已知的n个样本的核估计推导第n+1个样本的核密度估计,来实现核密度估计的实时更新。
3实时剩余寿命
3.1特征退化分布的计算
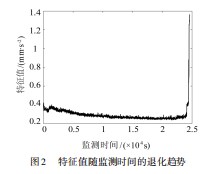
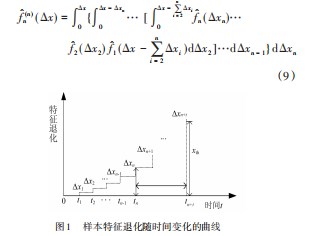
假设tn为轴承退化状态时间,可得到[0,tn]时间内所有退化样本的特征退化随时间变化的趋势可由图1所示。
为使设备的剩余寿命预测准确,由核密度估计可得[0,tn]随机退化增量的概率密度f者n(Δx),推出[0,tn]上随机退化增量累计特征退化量Δxn(令Δxn=nΔx)的f者n(n)(Δx),可由n重卷积得到:
3.2剩余寿命预测模型
设tn+t时刻,特征退化量达到Δxth(图1)时轴承失效。剩余寿命预测的实现,要对当前tn时刻的剩余寿命预测,通过初始时刻到当前tn时刻的退化量Δx 1:n(记Δxn=Δx(tn),Δx 1:n={Δx 1,Δx2,…,Δxn}),推出tn+t时刻的
退化量 Δx1:n (记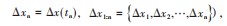
Δxn+t。设T为设备的剩余寿命,则剩余寿命的概率密度分布函数FT(t)为:

随着实时监测的进行,监测的样本数量不断增加,样本的核密度估计也不断更新。当使用非实时寿命预测模型时,基于这些样本的核密度估计必须为每一个新的样本数据重新计算,这导致历史样本不断被重新计算,计算量越来越大。为避免实时监测系统中样本核密度估计的重复计算问题,提出了一种递推核密度估计模型的实时更新算法,并对模型的特征退化分布和剩余寿命进行了连续的实时更新。
在实时变化的轴承下获得新的样本数据后,通过F(t)可推算出下一时刻的F(t+1),进而实现实时剩余寿命预测。
4实例分析
本文使用IEEE PHM2012提供的全寿命轴承数据对该模型进行了验证。该数据来自于FEMTO-ST研究中心的PRONOSTIA试验台的加速轴承寿命测试,振动信号的采样频率为25.6 kHz,采样时间为0.1 s,采样间隔为10 s,即每次获得2 560个数据样本。本文以Bearing 1-5在1 800 r/min和4 000 N载荷下的全寿命振动数据为例。在轴承故障诊断中,均方根(RMS)在实践中被广泛使用,因为它能更好地将轴承的退化状态反映出来。图2所示给出在时间变化下轴承的均方根特征退化趋势。从图中可看出均方根值基本上呈现出随时间单调上升的趋势,可以将轴承的退化趋势很好地展现出来。该轴承在t=2.463×104 s时出现故障,均方根的故障阈值为1.396 mm/s2。
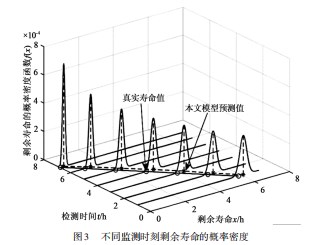
利用本文的模型预测轴承的剩余寿命,从图3可以看出,在轴承运行时间不断的变化下,接受到的样本数据逐渐越来越多,在核密度估计的剩余寿命模型不断的实时更新下,轴承的剩余寿命概率密度不断的增大且逐渐变窄,其方差也明显不断减小,可看出预测值与实际值相差不断减小,从而模型的准确性不断提高。
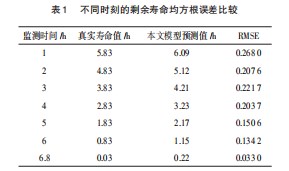
为了进一步评估所提方法的预测效果,表1所示为不同监测时间下实际剩余寿命和模型预测的平均剩余寿命的均方根误差(Root mean square error,RMSE)比较。从表中可看出,轴承在运行过程的实时预测下,预测值与真实值之间的RMSE在逐渐的减小,根据样本数据的增多,剩余寿命的预测值在不断的接近真实值,且误差也越来越小,从而可以验证本文模型对轴承寿命预测的有效性。
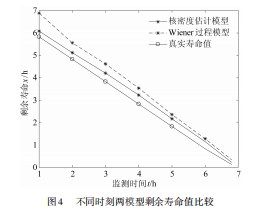
为了能验证本文模型在轴承应用上的优越性,将本文模型与Wiener过程的剩余寿命预测模型进行比较,Wiener过程多用于对具有非单调退化过程的设备进行建模。在相同条件下对轴承的退化过程进行寿命预测,得到图4所示不同时刻下本文核密度估计模型与Wiener过程模型的剩余寿命预测值和真实值之间的比较。从图中可看出,本文模型的预测结果相比Wiener过程模型,更加接近真实寿命值,随着时间的变化预测的准确性不断提高,从而验证了本模型的适用性和精确性。
5结束语
本文提出了一种轴承核密度估计的非参数剩余寿命预测方法,以解决预测设备剩余寿命时在不同样本分布下核估计的窗宽不能准确选择的问题。在该方法中,通过引入局部密度因子来选择核估计的窗宽,构建了一个自适应窗宽模型。该模型根据样本点的密度自适应地选择窗宽值进行核密度估计,即较小的窗宽用于样本点密集区,而较大的窗宽用于样本点稀疏区。随着接收到的实时监测数据的实时更新,核密度估计也自适应地递归更新,从而避免每增加一个样本数据就要进行一次计算带来计算量复杂问题。实例分析表明,随着样本数据的增加,所提模型的轴承剩余寿命预测值越来越接近实际值,并于Wiener过程模型比较,验证了本文模型的准确性和有效性。
参考文献:
[1]Wang H,Ma X,Zhao Y.A mixed-effects model of two-phase degradation process for reliability assessment and RUL predic‐tion[J].Microelectronics Reliability,2020,107(23):113622.
[2]Si X S,Wang W,Hu C H,et al.Remaining useful life estimation-A review on the statistical data driven approaches[J].European Journal of Operational Research,2011,213(1):1-14.
[3]王典.基于LSTM参数动态更新的滚动轴承剩余寿命预测[J].机电工程技术,2021,50(5):25-28.
[4]裴洪,胡昌华,司小胜,等.基于机器学习的设备剩余寿命预测方法综述[J].机械工程学报,2019,55(8):1-13.
[5]Wu J Y,Wu M,Chen Z,et al.A joint classification-regression method for multi-stage remaining useful life prediction[J].Jour‐nal of Manufacturing Systems,2021,58(3):109-119.
[6]喻勇,司小胜,胡昌华,等.数据驱动的可靠性评估与寿命预测研究进展:基于协变量的方法[J].自动化学报,2018,44(2):216-227.
[7]Si X S,Wang W,Hu C H,et al.Remaining useful life estimation–A review on the statistical data driven approaches[J].Europe‐an Journal of Operational Research,2011,213(1):1-14.
[8]Caio B,Marcio D,Lins I D,et al.Remaining Useful Life Estima‐tion by Empirical Mode Decomposition and Support Vector Ma‐chine[J].IEEE Latin America Transactions,2016,14(11):4603-4610.
[9]Pei H,Hu C,Si X,et al.Remaining Useful Life Prediction for Nonlinear Degraded Equipment With Bivariate Time Scales[J].IEEE Access,2019(7):165166-165180.
[10]刘文溢,刘勤明,周林森.基于高阶隐半马尔科夫模型的设备剩余寿命预测[J].计算机集成制造系统,2022,24(3):1-22.
[11]杨楠,周峥,陈道君,等.基于非参数核密度估计的风功率波动性概率密度建模方法[J].太阳能学报,2019,40(7):2028-2035.
[12]张卫贞,曾建潮,石慧,等.基于核密度估计的实时剩余寿命预测[J].计算机集成制造系统,2020,26(7):1794-1801.
关注SCI论文创作发表,寻求SCI论文修改润色、SCI论文代发表等服务支撑,请锁定SCI论文网!
文章出自SCI论文网转载请注明出处:https://www.lunwensci.com/ligonglunwen/46724.html

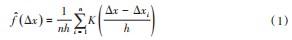
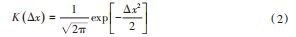
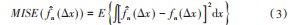
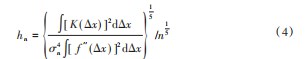
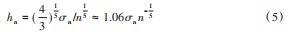

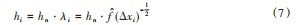
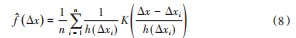


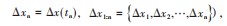 Δxn+t。设T为设备的剩余寿命,则剩余寿命的概率密度分布函数FT(t)为:
Δxn+t。设T为设备的剩余寿命,则剩余寿命的概率密度分布函数FT(t)为: