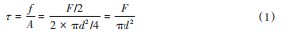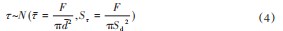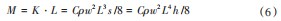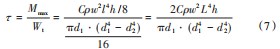SCI论文(www.lunwensci.com):
摘要:机械安全设计是一种基于机械设计理论和实验数据所进行的理论设计,如大家熟知的安全系数设计法,但安全系数的取值很大程度上取决于设计师的主观经验,存在一定的盲目性。机械可靠性设计是将设计中与结构应力、材料强度相关的参数均视为一定的分布函数,利用机械可靠性中的应力-强度干涉理论建立可靠度模型,继而根据应力与强度的分布关系算得结构的可靠性。以某种受组合应力的结构为例,将结构的载荷情况与结构自身强度视为一定分布的参数,采用机械可靠性理论建立了结构的应力-强度的可靠性模型,最后根据设定的可靠度置信区间来推得满足该可靠性要求的结构尺寸参数,相较于安全系数法的设计,这种设计能更为直观地表达出其结构在使用时的可靠性。
关键词:安全系数;机械可靠性;应力-强度干涉;组合应力
A Safety Design Method Based on Mechanical Reliability
Ouyang Jie,Yu Siyuan※
(Hangzhou Applied Acoustics Research Institute,Hangzhou 311400,China)
Abstract:Traditional mechanical safety design is a theoretical design based on certain design theories and experimental data.Such as the well-known safety factor design method,the method has a lot of subjectivity and a certain blindness.Mechanical reliability design treats the parameters related to structural stress and material strength as a distribution function.Based on stress-strength interference theory in mechanical reliability,and the reliability model is established.Finally,according to the set reliability confidence interval,then the reliability of the structure is calculated according to the distribution relationship between stress and strength.Taking a structure subjected to combined stress as an example,the load and strength of the structure were regarded as distributed parameters,and the reliability model of stress strength of the structure was established by using the mechanical reliability theory.The structure size parameters that met the reliability requirements were obtained according to the set confidence interval.Compared with the design of the safety factor method,the design could more intuitively express the reliability of the structure in use.
Key words:safety factor;mechanical reliability;stress-strength interference;combined stress
0引言
传统的结构机械设计方法为结构的理论设计,该设计方式主要是根据长期总结的设计理论和实验数据所进行的设计[1]。以某回转吊杆(为一种水下设备回转工装结构)的结构设计为例:除了需满足回转吊杆的使用要求以外,如下水深度、工程可操作,还需考虑结构的强度是否能满足使用。回转吊杆在工作时主要承受被吊物的重力、回转所需的扭矩,以及由于吊杆中心与被测物重心偏移所产生的弯矩,三力共同作用对吊杆产生了应力σ。当其应力大于吊杆材料的屈服强度σlim时,吊杆就会产生塑性变形,从而可以认为吊杆工作失效。因此设计时需要确保结构的所受应力应小于结构本身的屈服强度,即σ<σlim,同时工程应用时会根据以往类似结构设计实验数据来设定一定的安全系数S(大于1),以确保实际工作时结构应力小于结构的屈服强度,即Sσ≤σlim。其实在众多工程应用领域,往往都会根据实验数据来对相关的结构设置最低安全系数要求,并形成相关标准或准则,例如电梯的钢丝吊绳的安全系数标准要求在6倍以上[2]。而对于此种非标设计的工程结构,目前并没有使用的所需最低安全系数要求,并且由于回转吊杆在工作时受载荷的情况较为复杂,也难以用经验法来判断安全系数的设计数值。
机械可靠性设计与常规的安全系数法不同,它是将零件所受的载荷、工况、结构尺寸参数以及零件自身的强度都考虑为一定规律的函数分布[3-4]。在文献中,乐滨等[5]就分析了机械强度计算方法中采用的安全系数法存在的问题,而运用机械可靠性理论,得到机械可靠性与机械安全系数的关系。其将影响零件应力、强度的设计参数视为服从一定分布的随机变量,考虑了应力与强度的离散性,最后根据应力-强度干涉推导出零件不失效的概率数值。比如在本文中将吊杆直径尺寸D,其实际尺寸可以看做为以d值为均值,一定方差值的正态分布函数。此外,郑晓[6]介绍了一种过盈配合的机械可靠性模型,其将过盈联接强度、辊轴强度、辊体强度3种强度的可靠度视为一个串联系统,提出了基于系统可靠度的磨辊轴过盈联接可靠性设计模型。吴海淼[7-8]在两篇文章里都利用应力-强度干涉模型介绍了可靠性设计中不同的分布模型与安全系数之间的关系,并举例进行了计算,形象地表达了安全系数对应的可靠度。
上述文章基本都从理论上阐述了基于可靠性的安全设计方法,但基本都是简单的力学模型,针对复杂的组合应力并没有给出相应的解决措施。本文将从结构受力情况开始分析,建立回转吊杆的受力模型,以确定受力薄弱点的应力情况,并结合结构材料的相关可靠性参数,得到影响结构强度的建立回转吊杆的可靠性模型,最后利用应力-强度的干涉理论以及设置的置信区间推得满足该可靠性要求的结构参数。
1回转吊杆的结构
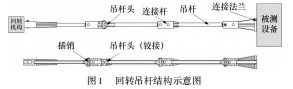
回转吊杆的结构主要由连接法兰、吊杆、插销、吊杆头等组成。吊杆底部连接法兰与入水设备对接,顶部与回转机构连接。结构示意如图1所示。求满足该结构强度要求的吊杆头及插销的尺寸参数。
回转吊杆的连接法兰与被测设备连接,并通过插销和连接杆将吊杆一节节连接起来以达到要求吊装要求的入水深度。回转吊杆在工作时主要受到被测设备的拉力、回转所需扭力。另外当被测设备外形不规则,实际质量重心难以确定时,回转吊杆的法线与重心的偏移会产生弯矩应力。为了降低或消除该弯矩应力的不利影响,在连接法兰与连接杆之间增加加强筋,另外将部分吊杆对接的部位的插销连接改为铰接的形式,如图1所示,该结构能够大大降低转动方向上的弯矩应力的影响。综上在本次设计分析时,可以将质量偏移产生的弯矩应力忽略不计。根据理论力学的分析,吊杆头与插销连接处的主要应力为拉、扭的组合应力。
2回转吊杆的应力分析
2.1连接处受力分析
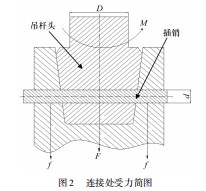
根据上节分析可知,回转吊杆的受力薄弱处位于吊杆插销连接处,下面针对吊杆头及插销进行应力分析。图2所示为连接位置的受力简图。
根据结构受力分析可知,吊杆头主要受拉、扭组合应力作用,插销受剪切力作用。
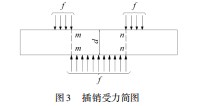
2.2插销的应力分析
首先对插销进行力学分析,其受力图如图3所示。图中插销中部相对于上下两端,在切面m-m和n-n两个面上错动,为双剪切。
根据材料力学可以算得插销横截面上的切应力为:
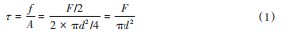 式中:F为被吊重物的水中重量;d为插销的直径尺寸,考虑到直径尺寸的加工公差正负a,可将直径视为均值为dˉ和方差Sd是与a相关的正态分布[4],记为:
式中:F为被吊重物的水中重量;d为插销的直径尺寸,考虑到直径尺寸的加工公差正负a,可将直径视为均值为dˉ和方差Sd是与a相关的正态分布[4],记为:
 则直径的概率分布函数的表达式为:
则直径的概率分布函数的表达式为:
 综上分析可知,插销的切应力也应符合正态分布的规律,其分布规律为:
综上分析可知,插销的切应力也应符合正态分布的规律,其分布规律为:
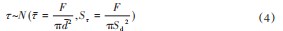 2.3吊杆头的应力分析
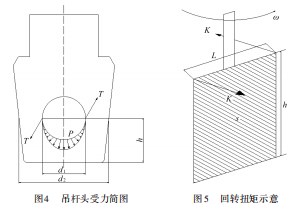
吊杆头主要受扭矩M产生的切应力τ以及压力F产生的压应力P的组合作用,其受力关系如图4所示。
2.3.1吊杆头切应力分析
回转扭矩如图5所示。其中扭矩M主要为被测物在水中转动时阻力形成的扭矩,根据流体力学相关知识,物体在水中旋转的阻力K为:
2.3吊杆头的应力分析
吊杆头主要受扭矩M产生的切应力τ以及压力F产生的压应力P的组合作用,其受力关系如图4所示。
2.3.1吊杆头切应力分析
回转扭矩如图5所示。其中扭矩M主要为被测物在水中转动时阻力形成的扭矩,根据流体力学相关知识,物体在水中旋转的阻力K为:
 式中:ρ为水密度;w为回转角速度;L为回转体横截面长度;s为垂直方向横截面积;C为阻力系数。
由式(5)可知,最大阻力在外径最大处,其扭矩值应为:
式中:ρ为水密度;w为回转角速度;L为回转体横截面长度;s为垂直方向横截面积;C为阻力系数。
由式(5)可知,最大阻力在外径最大处,其扭矩值应为:
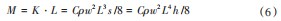 根据材料力学有关知识,吊杆头内孔处的扭矩M产生的切应力τ为:
根据材料力学有关知识,吊杆头内孔处的扭矩M产生的切应力τ为:
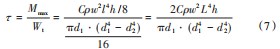 当回转物体为不规则形状时,L值取最大横截面长度尺寸;d1、d2为吊杆头设计的关键尺寸,其中d1是与插销外径d的配合尺寸,其主体尺寸可以视为一致,即d=d1。参考文献中的案例,可以将d1、d2认为是符合正态分布规律的参数:
当回转物体为不规则形状时,L值取最大横截面长度尺寸;d1、d2为吊杆头设计的关键尺寸,其中d1是与插销外径d的配合尺寸,其主体尺寸可以视为一致,即d=d1。参考文献中的案例,可以将d1、d2认为是符合正态分布规律的参数:
 将式(7)中,除d1、d2以外的参数视为一确切数值。即可得到吊杆头所受的切应力τ应符合与d1、d2相关的某一分布的参数。
2.3.2吊杆头的压应力分析
另外吊杆头内孔受到插销的压力如图4所示,是典型的材料力学中挤压力学模型,根据材料力学知识,该压应力p数值应为:
将式(7)中,除d1、d2以外的参数视为一确切数值。即可得到吊杆头所受的切应力τ应符合与d1、d2相关的某一分布的参数。
2.3.2吊杆头的压应力分析
另外吊杆头内孔受到插销的压力如图4所示,是典型的材料力学中挤压力学模型,根据材料力学知识,该压应力p数值应为:
 式中:A表为插销与吊杆头接触挤压面积,在此模型中,挤压面积为圆孔边缘到吊杆头外边缘的距离和吊杆头直径的乘积。
通过式(10)可知,考虑到其边缘距离的尺寸为变化值,可以近似看为随机正态分布,可以看出挤压应力是随挤压面积变化的变量,其最大的数值位于挤压面积最小的地方。
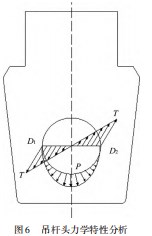
根据上述对吊杆头的扭矩以及压应力的分析,可以得到吊杆头在两种应力作用下的组合应力σ的状态。绘制吊杆头内孔力学特性图如图6所示。
D1和D2是内圆柱体表面任意两点,而其扭矩所产生的应力与其他边缘各点相同,截面受到不均匀的轴向应力作用(圆柱面中点处,挤压应力最大),回转吊杆的最大应力值应为挤压应力与扭应力组合值最大处,本次回转吊杆的最大应力处位于插销的顶点处,即其内孔外表面底点为是危险应力点。根据材料力学有关知识,可知吊杆头的内孔表面处应力σ应为:
式中:A表为插销与吊杆头接触挤压面积,在此模型中,挤压面积为圆孔边缘到吊杆头外边缘的距离和吊杆头直径的乘积。
通过式(10)可知,考虑到其边缘距离的尺寸为变化值,可以近似看为随机正态分布,可以看出挤压应力是随挤压面积变化的变量,其最大的数值位于挤压面积最小的地方。
根据上述对吊杆头的扭矩以及压应力的分析,可以得到吊杆头在两种应力作用下的组合应力σ的状态。绘制吊杆头内孔力学特性图如图6所示。
D1和D2是内圆柱体表面任意两点,而其扭矩所产生的应力与其他边缘各点相同,截面受到不均匀的轴向应力作用(圆柱面中点处,挤压应力最大),回转吊杆的最大应力值应为挤压应力与扭应力组合值最大处,本次回转吊杆的最大应力处位于插销的顶点处,即其内孔外表面底点为是危险应力点。根据材料力学有关知识,可知吊杆头的内孔表面处应力σ应为:
 由公式(11),便可以推导出应力σ的分布函数。考虑到本次结构应力情况较为复杂,影响结构应力的参数较多,为了便于计算在对回转吊杆中进行分析时,将对结构强度影响较小,且现实中参数范围波动较小的视为一恒定的量进行计算。即可得到吊杆头内孔表面应力为σ与d1、d2相关分布的参数,在本例中,d2与d1为同一零件上密切相关的两个结构尺寸,为了简化计算,可以将d2视为与d1正相关的分布,即:
由公式(11),便可以推导出应力σ的分布函数。考虑到本次结构应力情况较为复杂,影响结构应力的参数较多,为了便于计算在对回转吊杆中进行分析时,将对结构强度影响较小,且现实中参数范围波动较小的视为一恒定的量进行计算。即可得到吊杆头内孔表面应力为σ与d1、d2相关分布的参数,在本例中,d2与d1为同一零件上密切相关的两个结构尺寸,为了简化计算,可以将d2视为与d1正相关的分布,即:
 在此基础上即可理解为内应力σ是与d1相关的分布,且根据概率论的相关知识[10],正态分布的自身的平方以及加减后的分布也服从正态分布,即可将组合应力σ,也视为符合某正态分布的参数。
3回转吊杆的强度分析
回转吊杆的强度分布与材料特性有关,可根据材料手册查询回转吊杆所选材料的屈服强度分布状况[11],通常其符合正态分布规律:
在此基础上即可理解为内应力σ是与d1相关的分布,且根据概率论的相关知识[10],正态分布的自身的平方以及加减后的分布也服从正态分布,即可将组合应力σ,也视为符合某正态分布的参数。
3回转吊杆的强度分析
回转吊杆的强度分布与材料特性有关,可根据材料手册查询回转吊杆所选材料的屈服强度分布状况[11],通常其符合正态分布规律:
 4回转吊杆可靠性设计
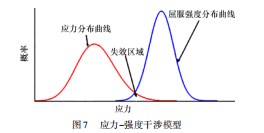
通过上文可知回转吊杆的设计应力与强度的分布规律,绘制其概率分布曲线,如图7所示。
将结构的应力大于材料的屈服强度时的情况定义为结构失效,则图中两曲线干涉区域即为可能发生失效的概率。在得到应力分布后,再通过查询的材料屈服强度分布,利用根据应力-强度干涉理论[12],可得到回转吊杆的可靠度数值即该结构不发生失效的概率值:
4回转吊杆可靠性设计
通过上文可知回转吊杆的设计应力与强度的分布规律,绘制其概率分布曲线,如图7所示。
将结构的应力大于材料的屈服强度时的情况定义为结构失效,则图中两曲线干涉区域即为可能发生失效的概率。在得到应力分布后,再通过查询的材料屈服强度分布,利用根据应力-强度干涉理论[12],可得到回转吊杆的可靠度数值即该结构不发生失效的概率值:
 分别计算插销的可靠度R1以及吊杆头的可靠度R2,则整个回转吊杆的可靠度为:
分别计算插销的可靠度R1以及吊杆头的可靠度R2,则整个回转吊杆的可靠度为:
 利用安全系数法设计时,可以设定一安全系数,再结合强度、应力强度推算得到满足该安全系数的参数。而在机械可靠性设计时,可对R吊设置一定的置信区间进而可以推导出与插销、吊杆头应力有关的变量参数。例如某符合一正态分布的参数,其基本分布在(μ-3σ,μ+3σ)范围内概率为0.997 4,在数学中将在此区间外的可以认为是随机误差,即大家熟知的3δ准则,可以设定3δ的置信区间为本次设计的结构可靠度要求,对R1、R2进行简单的可靠度分配后,便可以根据公式推算出达到此置信区间的变量参数。
5结束语
本文利用机械可靠性的分析方法,对回转吊杆结构的受力情况进行分析,继而分析影响回转吊杆使用可靠性的两个关键零件的应力情况,并进行合理的分布化,得到两个零件的应力分布情况,通过查询材料本身的强度分布参数并建立可靠性模型。将两个零件视为串联系统,利用应力—强度的干涉理论,推算得到结构满足一定可靠度置信区间的待定参数,即文中的插销直径。
相对于传统的安全系数设计的方法,机械可靠性设计方法能够很形象地表达结构件的应力与强度状况,从而定量地给出设计参考,也给工程应用中无安全系数设计标准的案例提供了一种设计思路。
参考文献:
[1]濮良贵,纪名刚.机械设计[M].北京:高等教育出版社,2005.
[2]GB8903-2005,电梯用钢丝绳[S].
[3]冉朝光,杨杰,李萌,等.机械可靠性设计方法的发展与研究现状[J].现代制造技术与装备,2015(5):177-178.
[4]刘混举.机械可靠性设计[M].北京:科学出版社,2012.
[5]乐滨,石端伟.基于可靠性的机械安全系数设计方法的探讨[J].武汉大学学报(工学版),2001,34(2):48-52.
[6]郑晓.磨辊轴过盈联接系统可靠性设计[J].机械设计与制造,2004(5):1-2.
[7]吴海淼,赵立新,姚贵英,等.基于平均安全系数的可靠性设计方法研究[J].机械设计与研究,2009,25(4):14-16.
[8]吴海淼,姚志辉,王凯,等.基于可靠性平均安全系数的设计方法研究[J].河北工程大学学报(自然科学版),2009,26(2):74-77.
[9]胡启国,刘元朋.机械可靠性设计及应用[M].北京:电子工业出版社,2013.
[10]熊德之,张志军.概率论与数理统计及其应用[M].北京:科学出版社,2007.
[11]成大先.机械设计手册[M].北京:化学工业出版社,2017.[12]王金武.可靠性工程基础[M].北京:科学出版社,2013.
关注SCI论文创作发表,寻求SCI论文修改润色、SCI论文代发表等服务支撑,请锁定SCI论文网!
利用安全系数法设计时,可以设定一安全系数,再结合强度、应力强度推算得到满足该安全系数的参数。而在机械可靠性设计时,可对R吊设置一定的置信区间进而可以推导出与插销、吊杆头应力有关的变量参数。例如某符合一正态分布的参数,其基本分布在(μ-3σ,μ+3σ)范围内概率为0.997 4,在数学中将在此区间外的可以认为是随机误差,即大家熟知的3δ准则,可以设定3δ的置信区间为本次设计的结构可靠度要求,对R1、R2进行简单的可靠度分配后,便可以根据公式推算出达到此置信区间的变量参数。
5结束语
本文利用机械可靠性的分析方法,对回转吊杆结构的受力情况进行分析,继而分析影响回转吊杆使用可靠性的两个关键零件的应力情况,并进行合理的分布化,得到两个零件的应力分布情况,通过查询材料本身的强度分布参数并建立可靠性模型。将两个零件视为串联系统,利用应力—强度的干涉理论,推算得到结构满足一定可靠度置信区间的待定参数,即文中的插销直径。
相对于传统的安全系数设计的方法,机械可靠性设计方法能够很形象地表达结构件的应力与强度状况,从而定量地给出设计参考,也给工程应用中无安全系数设计标准的案例提供了一种设计思路。
参考文献:
[1]濮良贵,纪名刚.机械设计[M].北京:高等教育出版社,2005.
[2]GB8903-2005,电梯用钢丝绳[S].
[3]冉朝光,杨杰,李萌,等.机械可靠性设计方法的发展与研究现状[J].现代制造技术与装备,2015(5):177-178.
[4]刘混举.机械可靠性设计[M].北京:科学出版社,2012.
[5]乐滨,石端伟.基于可靠性的机械安全系数设计方法的探讨[J].武汉大学学报(工学版),2001,34(2):48-52.
[6]郑晓.磨辊轴过盈联接系统可靠性设计[J].机械设计与制造,2004(5):1-2.
[7]吴海淼,赵立新,姚贵英,等.基于平均安全系数的可靠性设计方法研究[J].机械设计与研究,2009,25(4):14-16.
[8]吴海淼,姚志辉,王凯,等.基于可靠性平均安全系数的设计方法研究[J].河北工程大学学报(自然科学版),2009,26(2):74-77.
[9]胡启国,刘元朋.机械可靠性设计及应用[M].北京:电子工业出版社,2013.
[10]熊德之,张志军.概率论与数理统计及其应用[M].北京:科学出版社,2007.
[11]成大先.机械设计手册[M].北京:化学工业出版社,2017.[12]王金武.可靠性工程基础[M].北京:科学出版社,2013.
关注SCI论文创作发表,寻求SCI论文修改润色、SCI论文代发表等服务支撑,请锁定SCI论文网!
文章出自SCI论文网转载请注明出处:https://www.lunwensci.com/ligonglunwen/46722.html