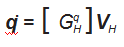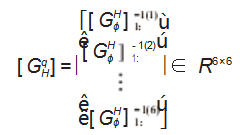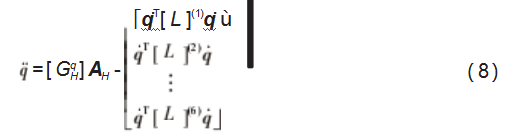SCI论文(www.lunwensci.com):
摘要:为了进一步发展并扩大并联机构的应用领域, 以一种结构相对简单且对称 、具有大工作空间快速运动特性的 6-PSS 并联机 构为研究对象, 对该机构运动学性能分析及机构结构尺寸参数优化方面展开了研究和探讨 。首先分析其结构特点并对其进行了尺 寸参数设计, 利用影响系数法求解得到机构一阶和二阶影响系数矩阵, 分析了机构的全域性能指标和全域波动性能指标 。以动平 台的长度和宽度作为变量对其进行了实例仿真分析, 分别获得相应的性能图谱, 通过对性能图谱分析和总结得到动平台长度和宽 度对机构运动性能的影响, 同理可得到其他尺寸参数对机构运动性能的影响 。通过比较分析并综合取舍可进行尺寸参数的优化, 进而提高机构的运动性能, 为实现机构尺寸的优化设计并提高机构运动性能提供了理论参考和一套简单 、实用的方法。
关键词 :并联机构; 影响系数; 性能指标; 优化设计
The Kinematic Performance Analysis and Size Optimization of MDOF Parallel Mechanism
Wang Chengfei, Chen He, Liu Dong
(China Shipbuilding Industry Corporation 723 Research Institute, Yangzhou, Jiangsu 225001, China)
Abstract: In order to further develop and expand the application field of parallel mechanism , a 6-PSS parallel mechanism which has relatively simple and symmetrical structure, large working space and fast movement characteristics was taken as the research object . The motion performance analysis and structure size parameters optimization of the mechanism were researched and discussed . Firstly, the structural characteristics and size parameters of 6-PSS parallel mechanism were described in details. The first and second order influence coefficient matries were obtained by the influence coefficient method, and the mechanism's global performance indicators and performance fluctuation indicators were analyzed. An example simulation analysis was carried out with the length and width of the moving platform as variables , and the corresponding performance maps were obtained repectively. The influence of the length and width of the moving platform on the kinematic performance of the mechanism was obtained by analyzing and summarizing the maps . Similarily, the influence of other size parameters on the kinematic performance of the mechanism could be obtained. Through comparative analysis and comprehensive selection the size parameters can be optimized to improve the kinematic performance of the mechanism . So that, a theoretical reference and a set of simple and practical methods were proposed to realize the optimal design of the mechanism size and improve the kinematic performance of the mechanism .
Key words: parallel mechanism; influence coefficient; performance indicator; optimal design
0 引言
随着科技的日益进步和生产自动化程度不断提高, 基于多支链的并联机构以其结构简单 、刚度大 、承载能 力强 、运动精度高且速度快 、易于控制等良好特性适应 了生产发展的需要, 并受到了国内外众多专家和学者的 重点关注 。 目前, 并联机构已经在工业自动化 、航空航 天 、医疗和测量等领域中不同场合都得到了成功应用。
运动性能分析是并联机构研究领域的重要内容, 对 机构的设计和优化及控制策略的选择具有重要意义, 国 内外很多学专家学者进行了大量研究 。Angeles 等[1]和 Cosselin 等[2]对机构性能指标和机构优化设计进行了研究 。高峰 、刘辛军 、郭希娟 、余梅生等基于一阶和二阶 影响系数对机构性能指标的研究做了大量贡献[3-7], 此外 杨育林 、陈海真 、高彦锟 、石志新等基于机构性能指标 的研究上对机构结构参数优化问题进行了研究[8- 11] 。 因 机构的尺寸参数的多维性和性能指标的严重非线性, 尽 管做了大量研究, 但仍有大量问题没有解决, 影响了机 器人机构的开发和应用。
6-PSS 并联机构不仅具有刚度大 、承载能力强和精 度高等通用特点, 还具有机构相对简单 、对称 、大工作 空间及快速运动的特点 。该机构在运动模拟器 、并联机 床 、微动机器人 、航空航天及医学等领域有着广泛应用前景 。本文首先对该 6-PSS 并联机构进行了参数化设计, 随后对该机构的运动学及运动学性能进行了分析, 提出 优化目标, 对其结构尺寸参数进行了优化, 大大提高了 该机构的综合运动性能。
1 机构的描述与坐标系建立
6-PSS 并联机构由运动基座 (安装有导轨)、 滑块、 球铰 、动平台 、执行器 (支杆) 以及拉杆等组成 。如图 1 所示, P 为与动平台固连的执行器末端的几何中心, 其 在动平台的投影为 Q; Pi 为移动副, 这里称为滑块; Li 为 6 根定长的拉杆; SAi 和 SBi 为球铰副, 安装在 6 根拉杆 的两端, 分别连接了 6 个滑块和动平台 。导轨 、滑块和 上 、下球铰关于平面 XOZ 对称 。该并联机构由 6 个安装 有直线电机的滑块为输入, 带动拉杆 、动平台一起运动, 实现执行器按照给定的可控的运动规律运动 ( 3 个移动 和 3 个转动的任意一种或者组合)。
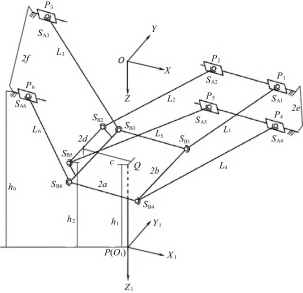
图 1 6-PSS 并联机构
假设执行器相对于各坐标轴无转动和移动时为机构 的初始位形, 以初始位形时执行器轴线在导轨平面的投 影点为原点建立固定坐标系 O-XOZ, 垂直导轨平面向下 为 Z 轴, X 轴与导轨平行指向 P1 一侧, 右手定则确定 Y 轴; 以执行器末端几何形心 P为原点建立动坐标系 O 1 - X1 Y1 Z 1, 初始方位和固定坐标系相同, 随执行器一起 运动。
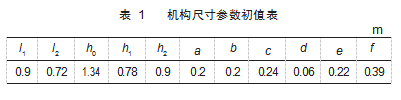
该并联机构结构尺寸主要有 11 个参数: 整个机构 的高度 (执行器末端到导轨平面的距离) h0, 两侧导轨 间距离的一半 e 和f, 拉杆的长度 l1 和 l2, 动平台长度 (下球铰 SB4 到 SB6 的距离) 为 2a, 动平台宽度 (下球铰 SB1 到 SB4 的 距 离 ) 为 2b, 下 球 铰 SB2 ( SB5 ) 到 平 面 Y1 O 1 Z 1 的距离 c, 下球铰 SB2 到 SB5距离的一半 d, 下球铰 SB2 ( SB5 ) 到平面 X1 O 1 Y1 的距离 h2, 平面 SB1 SB3 SB6 SB4 到平面 X1 O 1 Y1 的距离 h1 。初步确定机构尺寸参数如表 1 所 示, 其中拉杆 L1 、L3 、L4 、L6 的长度取 l1, 拉杆 L2 、L5 的 长度取 l2。
2 影响系数的求解
对于 6-PSS 并联机构, 因其机构结构上具有对称性 且支链具有相似性及对称性, 以机构第 1 支链为例 。如 图 2 所示, 按主动件到末端执行器, 依次求得支链 1 简化 并用单自由度转动副替换化后各运动副轴线方向的单位矢量分别为:
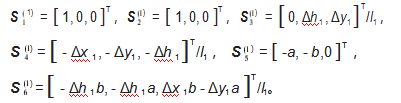
于是, 可以求得 6-PSS 并联机构支链 1 的一阶影响系数矩阵
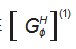
:

式中: P 为动平台末端执行器 P点在固定坐标系的位置 矢量; Rj (j=SA1 、SB1 ) 为运动副在固定坐标系的位置矢 量; P-Rj 为末端执行器 P点对支链 1 各运动副轴线的位 置矢量。

图 2 6-PSS 并联机构支链 1 运动副简化图
其余 5 条支链的一阶影响系数矩阵求法与支链 1 的 求法类似 。首先简化, 然后把对应运动副轴线向单位矢 量 Si)及矢量( P - Rj )(i)进行相应的替换即可 。每条支链 的一阶影响系数矩阵都是 6×6 矩阵, 则该并联机构共有 6 个 6×6 的一阶影响系数矩阵。
当已知动平台的运动时, 支链 i 各运动副的速度和平台速度的关系为:
ϕ̇(i) =
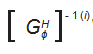
(i)VH i = 1, 2, ⋯, 6 ( 2 )
式中: VH = [ ω hx , ω hy , ω hz , VPx , VPy , VPz ]T, 为动平台速度矢 量; ϕ̇(i) = [ ϕ 1 , ϕ 2 , ϕ 3 , ϕ 4 , ϕ 5 , ϕ 6 ]T, 为支链 i 各运动副组成的速度矢量。
以 6 个移动副为主动输入件的运动方程如下:
ϕ̇i) =

VH i = 1, 2, ⋯, 6 ( 3 )
式中: ϕ̇i)为输入的广义速度, 其上下角分别表示所在的支链序号和支链中运动副的序号;
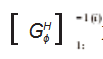
为第 i 条支链 的逆矩阵
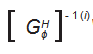
的第一行。
将上式以矩阵形式表示为:
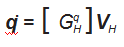
( 4 )
式中: q̇ = [ ϕ 1) , ϕ 2) , ϕ 3) , ϕ 4) , ϕ 5) , ϕ 6) ]T 为 6 个主动输入件滑块的独立广义速度矢量矩阵。
非奇异矩阵 [ G]定义为:
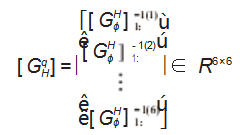
对式 ( 4 ) 求逆, 于是有:
VH = [ G ]q̇ ( 5 )
式中: [ G ] = [ G]- 1 为并联机构的一阶影响系数矩阵。
已知支链上 6 个主动输入运动副的相对加速度时, 其与动平台加速度的显式解析式可以表示为:
ϕ̈) = [ G] -β:1(i) ( AH - ϕ̇T (i) [ H](i)ϕ̇(i)) i = 1, 2, … , 6 ( 6 )
式中: ϕ̈) 为支链 i 上第β 个运动副相对加速度; [ Gϕ ] -β:1(i) 为第 i 支链一阶影响系数矩阵的逆矩阵的第β 行。
由式 ( 3 ) 和式 ( 5 ) 联立得到支链 i 各运动副相对 速度与广义速度的关系为:
ϕ̇(i) = [ G]- 1(i) [ G] q̇ i = 1, 2, … , 6 ( 7 )
已知并联机构的每条支链的第一个运动副为主动输 入件, 由于机构完全对称, 联合式 ( 7 ) 将式 ( 6 ) 化简 归并为一个式子:
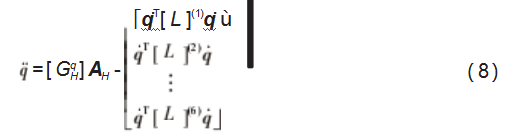
式中: = [ ϕ̈1) , ϕ̈2) , ϕ̈3) , ϕ̈4) , ϕ̈5) , ϕ̈6)]T 为该 机 构 的 广 义 加 速 度 矢 量 ; [ L ](i) 为 6 × 6 的 标 量 矩 阵 , 有 [ L ](i) = [ [ G]- 1(i) [ G] ]T [ [ [ G] ]T ∗ [ Hϕ ](i) ] [ G]- 1(i) [ G],i = 1, 2, … , 6, 其中 “∗” 是矩阵的 广义 标量积, 相当于把 前面的矩阵以常数来乘以后面矩阵的元素。
对式 ( 8 ) 进一步简化, 得:
= [ G] AH - q̇T [ H] q̇ ( 9 )
式中: [ H]矩阵为 6×6×6 的标量矩阵。
因此, 动平台的加速度用对广义坐标的二阶影响系数表示为:
AH = [ G] + q̇T [ H] q̇ ( 10 )
式中: 机构对广义坐标的二阶影响系数矩阵可以表示为
 3 运动学性能指标分析
3 运动学性能指标分析
机构运动学性能指标包括线速度 、角速度 、线加速 度和角加速度性能指标 。线速度 、角速度由机构的一阶 影响系数决定, 而线加速度和角加速度受机构的一阶、 二阶影响系数共同决定 。其条件数用一阶 、二阶影响系 数依次表示为:

式中: | |为矩阵的 Frobenius 范数; 上标“+”为矩阵的 广义逆矩阵; K 为条件数, 且 1 ≤ K < ∞; aq 、bq 为误差 系数, 均小于 1 (用于综合性能指标的计算时常取为 0.02 ); Gυ 、Gω 分别为一阶移动影响系数矩阵和一阶转动 影响系数矩阵; Hυ 、Hω 分别为二阶移动影响系数矩阵和 二阶转动影响系数矩阵, 其与影响系数之间的关系为 G = [ Gω , Gυ ]T , Hq = [ Hω , Hυ ]T。
一阶 、二阶影响系数矩阵的条件数随着机构的位形 的不同而变化, 在机构的工作空间内不同的点, 其条件 数是不同的, 这样无法准确地描述机构运动性能好坏 。 鉴于此, Gosselin 在工作空间的基础上提出了全域性指 标, 定义机构速度和加速度的全域性能指标为:

式中: i ∈ { Gω , Gυ , Gω + Hω , Gυ + Hυ }; W 为末端执行器的 可达工作空间; ηj 为全域性能指标, 1 ≥ η i > 0, ηj 的值 越大, 机构灵巧度和控制精度越高, 机构的运动学性能 也越高。
η 的大小可以反映机构在整个工作空间内运动性能 的平均水平的高低, 但它仅反映了机构在整个工作空间 内平均运动性能的情况, 并不能体现出在整个工作空间 内性能波动幅度的信息, 于是提出条件数倒数的均方差 为全域性能波动指标[9]:
 4 实例分析及尺寸优化
4 实例分析及尺寸优化
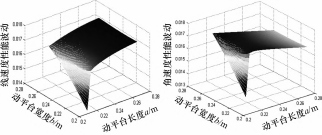
现在保持其他结构参数值不变, 改变机构的动平台 的长度和宽度这两个结构参数值为例, 对机构的线速度 和角速度性能指标进行仿真 。让 a=200~300 mm, b=200~ 300 mm, 步长都取为 20 mm, 组成 36组机构位形; 对每 组机构位形的每个自由度在可达工作空间空间中均匀取 均取 100个点进行仿真计算, 绘制全域性能图谱如图 3和 图 4所示。

(a) 线速度 (b) 角速度

(c) 线加速度 (d) 角加速度
图 3 全域性能图谱
 (a) 线速
(a) 线速 (b) 角速度

(c) 线加速度 (d) 角加速度
图 4 全域性能波动图谱
由图 3 可以看出, 机构的线速度 、角速度 、线加速 度和角加速度性能指标在左上方较大, 右下角较小 。即 在一定范围内, 当动平台长度尺寸变小 、宽度尺寸变大 时, 6-PSS并联机构的线速度 、角速度输出误差越来越 小, 机构的运动学指标越来越好 。从图 4 中可以得到机 构运动性能波动随着动平台尺寸变大而变大, 但动平台 宽度对其性能的影响相对较小 。 同理可求其他尺寸参数 对机构运动学性能的影响, 最终得到最优的机构尺寸和 控制策略。
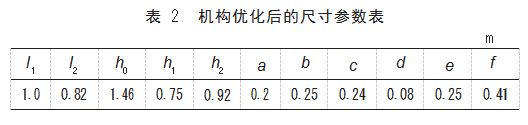
对于机构中动平台的尺寸参数, 综合考虑上述分析 得出的全域性能和全域性能波动图谱, 确定动平台的长 度参数为 a=0.2 m, 动平台的宽度参数 b=0.25 m。同理可 以对机构的其他尺寸参数进行优化, 最终得到优化后的 机构尺寸参数如表 2 所示, 此时 6-PSS 机构性能指标值 如表 3所示。
5 结束语
本文以 6-PSS 机构为研究对象, 对该机构运动学性 能分析及机构结构尺寸参数优化方面展开了研究和探讨。 首先分析了其结构特点并建立坐标系同时进行了尺寸参 数设计, 利用影响系数法求解出一阶 、二阶影响系数矩 阵, 对运动学性能的全域性能指标及全域性能波动指标 进行了分析 。然后以动平台的宽度和长度尺寸为实例分 析, 得到了相应的全域性能及全域性能波动图谱, 通过 分析图谱得到机构结构尺寸参数对运动性能的影响规律。 同理可得到其他尺寸参数对机构运动性能的影响, 进而 能够综合取舍进行尺寸参数的优化, 提高机构的运动性 能, 为实现机构的尺寸优化并提高机构性能提供了理论 参考和一套简单 、实用的方法。
参考文献:
[1] O Ma, J Angeles. Optimum Architecture Design of Platform Ma⁃ nipulators[C]//Fifth International Conference on Advanced Ro⁃ botics, 1991.
[2] C M Gosselin, Lavoie Eric. On the Kinematic Design of Spherical Three Degree-of-Freedom Parallel Manipulators[J]. The Interna⁃ tional Journal of Robotics Research, 1993,12(4):394-402.
[3] Gao F, Liu X J. The Relationships Between the Shapes of theWork-spaces and the Link Lengths of 3-DOF Symmetrical Pla⁃ nar Parallel Manipula-tors[J]. Mechanism and Machine Theory, 2001, 36(2): 205-220.
[4] Liu X J, Jin Z L, Gao F. Optimum Design of 3-DOF Spherical Parallel Manipulators with Res-pect to the Conditioning and Stiffness Indices[J]. Mechanism and Machine Theory, 2000, 35 (9): 1257-l267.
[5] 郭希娟,黄真 . 并联机器人机构加速度的性能指标分析[J]. 中 国机械工程,2002,13(24):2057-2091.
[6] 余梅生,朱思俊,郭希娟,等 . 空间双回路 RSSR-SC机构的速度、加速度性能指标分析[J].机器人技术与应用,2002(3):26-31.
[7] 郭希娟 . 机构性能指标理论与仿真[M]. 北京:科学出版社 ,2010.
[8] 杨育林,黄世军,刘喜平,等 .2-RUUS 机构动力学性能分析[J]. 机械工程学报,2009,45(11): 2-9.
[9] 陈海真,邹忠月,宋宏鹏 . 基于灵巧度 3-RCR 并联机器人机构 的结构参数优化[J]. 机床与液压,2012, 40(5):22-24.
[10] 高彦锟 ,刘忠途 ,程源 . 按照性能指标进行机构优化设计[J]. 机械科学与技术,2002(12):1600-1608.
[11] 石志新,罗玉峰,陈红亮,等 .机器人机构的全域性能指标研究 [J].机器人,2005,27(5):420-422.
关注SCI论文创作发表,寻求SCI论文修改润色、SCI论文代发表等服务支撑,请锁定SCI论文网!
文章出自SCI论文网转载请注明出处:https://www.lunwensci.com/ligonglunwen/46565.html

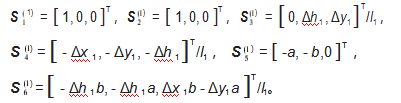
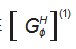 :
:

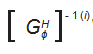 (i)VH i = 1, 2, ⋯, 6 ( 2 )
(i)VH i = 1, 2, ⋯, 6 ( 2 ) VH i = 1, 2, ⋯, 6 ( 3 )
VH i = 1, 2, ⋯, 6 ( 3 )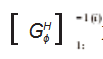 为第 i 条支链 的逆矩阵
为第 i 条支链 的逆矩阵 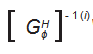 的第一行。
的第一行。