SCI论文(www.lunwensci.com):
摘要:交通强国的时代战略,大力推动着交通运输业的前进与发展,一带一路的时代战略又要求着对中西部的大力开发。我国国土面积庞大,地形多样,尤其是中西部地区,山地,峡谷,山壑等地形连绵不断。因此,跨越能力大,结构整体性好,耐久性好,构造简单的大跨径连续钢构桥受到了行业的大量关注。但是历史上因稳定性问题而发生的大跨进连续钢构桥事故层出不穷,严重威胁着国家与人民的经济与生命安全,所以桥梁稳定性的研究显得格外重要。
关键词:桥梁;稳定性;分析方法;稳定评价
1引言
随着学者们对桥梁稳定性研究的不断深入,连续钢构桥的受力特性分析越来越全面且综合,从平面到空间,从线性分析到非线性分析,从动力影响到静力影响,并且综合考虑到风,水,温度,混凝土徐变,地震,行车振动等。由于复杂的受力情况,使得我们使用原本传统的理论计算方法已经难以实现对桥梁稳定性的分析,需要采用更加合理且有效的新的方法。现在,在很多时候我们会选择使用有限元软件,通过模型的建立与分析来处理问题。张新军等人,建立大跨度钢桥梁在斜方向风的作用下的三维非线性静风稳定性分析方法;兰树伟等人,研究了轴力面积大小对非规则双层双柱式高墩桥梁体系临界力的影响,提供了快速计算的方法和公式,并且利用有限元Ansys进行了验算;李大龙等人,对河流冲刷下桥梁桩基稳定性的进行研究采用了三维分析方法;蔡建刚等人,利用有限元建模比较,提出一种改进的二维静风失稳模型。王领军,研究了各影响因素对斜拉桥稳定性的影响,同样采用了有限元法建立结构模型。在对大跨径连续钢构桥的稳定性的研究,越来越多的方法与手段被利用与发掘。
2稳定性分析基本理论
结构不稳定指的是在外力作用下,结构的稳定平衡状态突然变化,结构发生变形,失去正常承载力或无法正常工作的现象。结构稳定性问题分为平衡分支问题(第一不稳定性)和极值问题(第二不稳定性)两种。
2.1两类稳定问题的具体分析
2.1.1平衡分支问题
结构保持原有平衡状态的前提下,在所受荷载达到极限时,还出现了新的平衡状态。当理想轴压力杆的应力在临界状态下达到a点时,存在平衡形式的分支,存在两种平衡形式。实际的受压构件与理想的受压构件时存在一定的差异的。初始弯曲和偏心在力的作用下会发生数次。压缩弯曲状态仅在压力下发生。曲线3所示的是实际的荷载变形曲线。弯曲在压力P没有达到极限值是便开始发生了。初始偏心距和初始弯矩方向确定,所以变形方向也确定。即第一不稳定性。
2.1.2极值性问题
作用在结构上的荷载,在达到临界值后,即使保持不变或减小,结构也会失稳而发生变形的现象。塑性材料构件的压缩一侧,因为初始偏心和初始弯曲,轴向力未达到极限值时,形成塑性软化区。随着承受荷载的不断增大,弹性区慢慢减小,弯曲刚度减小,变形以非常快的速度增大。膨胀初始阶段,切线模量为正,压力、变形上升。然而,如曲线4和5所表示,在压力低于弹性压杆的极限值,变形增加,切线模量为负。这种不稳定性被称为极值性问题,即第二不稳定性。
3稳定问题的分析方法
静力平衡法(欧拉法),能量法,缺陷法,动力法和有限元法,是目前分析桥梁稳定性最经典的几种方法。
3.1静力平衡法(欧拉方法)
静力平衡方法利用理想化的轴心受压杆,基于静力平衡关系建立线性微分方程,并通过求解线性微分方程导出欧拉方程的分析方法。中心受到直杆的临界力的影响,杆端的拘束越强,杆的弯曲阻力越强,其临界力越大。由此,获得了能够对各种棒端的拘束状况统一细长直棒的中心受到压力的临界力的欧拉式的形式:

;式中:

—与边界条件有关的系数;—结构的刚度;—构件的长度。从上面的公式中发现,只有结构约束条件,刚性和长度会影响欧拉负载,而和假设为理想材料的材料的应力-变形曲线不会影响,这可以称为第一弹性弯曲的稳定性问题。
3.2能量法
结构总势能方程式:
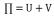
;式中:
 —体系的应变能;V—荷载势能。
—体系的应变能;V—荷载势能。
结构在初始平衡状态下,位置发生很小的变化,总势能会有增量。在最小势能原理的基础上,真正的连续系统被有限独立系统代替。
结构极限荷载,通过建立新的弯曲平衡,改变求解模型来解决。这里采用能量法中的Rayleigh-Ritz法分析。杆在具有无尽自由度的情况下,变形曲线通常采用广义坐标来表示,即

;式中:

—广义坐标;
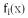
—坐标函数。
其中,广义坐标是独立的,坐标函数在满足杆端的位移条件的前提下,可以随意假定。

可以通过势能驻值条件来确定,并且通过势能驻值原理
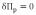 。
。
3.3缺陷法
我们一般都是在理想体系中考虑的平衡分支问题。然而,真实的结构并不能完全满足这些条件。实际杆件肯定会拥有初始弯曲,或许还拥有横向荷载,而且所受压力肯定存在偏心。实际杆件在受到荷载时,一开始,杆件变形会与荷载大小成正比,但开始比较缓慢,一段时间后会加剧,并且初始缺陷越大的杆件,变形越大。所以当杆件本身的缺陷就很大时,即使所受的荷载远低于欧拉荷载,也可能由于变形而毁坏。因此,如果荷载远小于欧拉荷载,初始缺陷较大的零件也可能会失效。
3.4动力法
在轴力的作用下处于平衡状态的构件,由于受到外力,会产生振动。结构会根据振动的收敛与发散,处为稳定平衡与不稳定平衡状态。其中使振动收敛的最大轴力为极限力。近似求解方法是我们目前用于桥梁稳定性分析常用的。主要分为两种,一种是从微分方程出发,一种是根据能量原理的近似方法。
3.5有限元法
这里从有限元的历史和发展作简单介绍。起初,人们热衷于用各种力学理论研究结构构件的力学行为。因此,基于“平衡”、“几何”和“本构”三个方程的分析方法横空出世,即弹性力学方法。弹性力学方法,其实就是通过计算位移,推出应力,应变等,需要求解出微分方程的边值问题。
其中,“平衡”方程和“几何”方程几乎都是微分方程(组)。虽然力学方法的理论简单直接,但结果也是最准确的。然而,对于稍微复杂的结构,将遇到复杂的微分方程。慢慢的,微分方程借助与猜测位移和引入能量原理,从大家的关注点中渐渐消失。
可以通过积分来分析结构。再之后,矩阵的引入使得计算变得高效。矩阵的引入与有限元的核心原理关系不大,但它很容易作为一种工具使用。人们用矩阵改写了分析过程,使现代有限元充满了矩阵运算。后来,人们对操作过程中的一些关键元素进行了命名,如单元刚度矩阵。例如,将每条曲线分成许多复杂的直线就足够了。与此类似,结构被分成许多部分,以猜测每个部分的位移。例如,它是线性的。只要结构划分足够多,每个部分是否准确并不重要。在保证单元间几何协调的前提下,计算的位移与实际位移非常接近。这样可以大大减少位错位移对最终结果的影响。这是有限元发展的另一个重要里程碑。因此,有限元理论基本上构建完整。现在,又制定了许多标准单元。每种单元都事先给定了假设的位移,并将结构划分为一定数量的标准单元进行分析,即有限元法。
就这样,有限元诞生了。此后,在计算机的大力支持下,有限元从一个繁琐的辅助工具逐渐成为结构分析的重要手段。一般来说,有限元是结构计算的一种近似方法。其核心在于弹性力学的基本分析,能量原理和数值积分的引入,以及结构的离散化以保证精度。
3.5.1有限元法分析的一般步骤
(1)结构模型化。
结构的模型化就是使用各种简化处理,用计算模型来表示实际结构。
使用各种简化处理,用计算模型来表示实际结构。
(2)结构的离散化
结构的离散化是指,在结构建模后,将需要处理的结构物割据为有限个单位体,在单位体的指定点设置接点,使联结单位的关联参数具有一定的连续性,构成代替原始结构的单位的集合体。单元体的大小和接点的位置决定,必须充分考虑结构受力状况和施工中的单元区分。
(3)选择位移模式
(4)分析单元的力学特性
位移模式选定后,可以从三个部分进行单元的力学特性分析:
①结点位移表示的单元应变关系式:
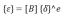
;式中:

—单元内任一点应变列阵;
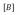
—单元应变矩阵。
②结点位移表示的单元应力关系式:

;式中:

—单元内任一点应力列阵;
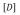
—与单元材料有关的弹性矩阵。
③单元的平衡方程为:

;式中:

—单元坐标系下的单元刚度矩阵,遍布整个单元体积,且

;当单元坐标系与结构坐标系不同,用坐标转换矩阵[t]进行转换,即:
 。
。
(5)建立整个结构的平衡方程
整体刚度矩阵[k],荷载列阵[f]以及整个结构的点位移向量

之间的整体平衡方程:

。
(6)求解未知结点位移
计算方法的选择,要根据几何边界条件和方程组的特点来选择,最后根据步骤5,解出未知位移。
(7)计算单元应力
利用己求解出的结点位移,由步骤4计算各单元的应力。
4稳定的评价指标
稳定安全系数是最直观的稳定评价。在一般情况下,结构的稳定安全系数是针对某个特定的负荷。在非线性稳定性分析中,还没有统一的依据来选择加载方案。在一般情况下,稳定安全系数的计算有两种方法:
稳定安全系数为: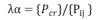
这两个稳定的安全系数可以反映稳定的安全储备。第一个定义反映了结构对所有载荷的安全储备能力。第二个定义将现有结构的稳态荷载视为不可变的,仅考虑结构的新稳态荷载或活动荷载的安全存储容量。
根据《公路钢筋混凝土及预应力钢筋混凝土桥涵设计规范》(JTG 3362-2018)。
结构重要系数:1.1;荷载系数取:1.2;材料的安全系数:1.25;结构的工作条件系数:0.95;结构的总体系数:

。根据相关规范,在容许应力法计算时,要求1.7。按《公路斜拉桥设计规范》(JTGT3365-01—2020)中规定结构的安全系数4。一般情况下,进行非线性稳定分析时,稳定安全系数应满足上述要求。
5提高桥梁稳定性措施
(1)提高耐久性是提高桥梁稳定性的重要手段。要想提高耐久性,首先,要从材料出发,使用高强度混凝土。其次,设计上要加以重视,把控好细节设计,不能掉以轻心。
(2)打好基础。桥梁建设,基础尤其关键,要根据地质和环境条件,在选择符合要求的材料前提下,设计好混凝土桩的打入深度和间距,严格执行,不能有分毫差错。细节决定成败的道理要牢记在心。尤其是高墩桥梁,绝对不能允许桥墩倾斜的出现。
(3)施工阶段也尤其重要。在施工时,要提醒施工人员小心谨慎,切忌遗漏一些细小零件的组装,施工阶段避免对桥梁结构的伤害。
(4)做好防水,排水。桥梁表面和重要结构上可以涂上防水涂层,并且排水系统要设计完善,避免积水现象的发生。如果遭遇特大自然灾害,要及时处理解决。
(5)对连接点进行加固。在结构的连接处,可以用焊接或者加肋的方式进行巩固。
(6)避免桥梁超载。最年来,因为超载而导致的桥梁倾覆事故层出不穷,桥梁交付完工后,在使用阶段要严格把控行车的重量荷载,杜绝超载现象,以免造成难以发现的结构性损伤,而导致无法预测的灾难。
(7)定期对桥梁的各个构件进行检查以及养护。由于桥梁长期暴露在自然中,自然中各个因素对桥梁结构以及材料不断侵蚀,所以定期的检查以及养护维修显得尤其重要。及时发现损坏部分,加以修补,是提高桥梁稳定性的重要举措。
(8)若条件允许,可以对桥梁进行监控监测设计。监控监测可以随时查看桥梁的变形,裂缝,受力状态,结构稳定情况,观测出外力对桥梁的影响,比如:风,水等等。可以起到预警与防治作用。
6结论
(1)本文阐述了稳定性分析的基本理论。
(2)解析了两类稳定问题的具体区别,即平衡分支问题以及稳定性问题。
(3)对桥梁稳定性分析的经典方法进行了详细的介绍。
(4)给出了稳定性的一般评价标准。
(5)例举了一些提高桥梁稳定性的方法与措施。
关注SCI论文创作发表,寻求SCI论文修改润色、SCI论文代发表等服务支撑,请锁定SCI论文网!
文章出自SCI论文网转载请注明出处:https://www.lunwensci.com/ligonglunwen/43475.html

 ;式中:
;式中: —与边界条件有关的系数;—结构的刚度;—构件的长度。从上面的公式中发现,只有结构约束条件,刚性和长度会影响欧拉负载,而和假设为理想材料的材料的应力-变形曲线不会影响,这可以称为第一弹性弯曲的稳定性问题。
—与边界条件有关的系数;—结构的刚度;—构件的长度。从上面的公式中发现,只有结构约束条件,刚性和长度会影响欧拉负载,而和假设为理想材料的材料的应力-变形曲线不会影响,这可以称为第一弹性弯曲的稳定性问题。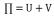 ;式中:
;式中: —体系的应变能;V—荷载势能。
—体系的应变能;V—荷载势能。 ;式中:
;式中: —广义坐标;
—广义坐标;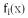 —坐标函数。
—坐标函数。 可以通过势能驻值条件来确定,并且通过势能驻值原理
可以通过势能驻值条件来确定,并且通过势能驻值原理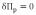 。
。
 ;式中:
;式中: —单元内任一点位移阵列;
—单元内任一点位移阵列; —形函数矩阵;—单元的结点位移阵列。
—形函数矩阵;—单元的结点位移阵列。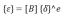 ;式中:
;式中: —单元内任一点应变列阵;
—单元内任一点应变列阵;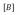 —单元应变矩阵。
—单元应变矩阵。 ;式中:
;式中: —单元内任一点应力列阵;
—单元内任一点应力列阵;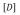 —与单元材料有关的弹性矩阵。
—与单元材料有关的弹性矩阵。 ;式中:
;式中: —单元坐标系下的单元刚度矩阵,遍布整个单元体积,且
—单元坐标系下的单元刚度矩阵,遍布整个单元体积,且 ;当单元坐标系与结构坐标系不同,用坐标转换矩阵[t]进行转换,即:
;当单元坐标系与结构坐标系不同,用坐标转换矩阵[t]进行转换,即: 。
。 之间的整体平衡方程:
之间的整体平衡方程: 。
。 ;式中:
;式中: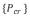 —结构总的失稳荷载;
—结构总的失稳荷载;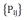 —结构的实际荷载。
—结构的实际荷载。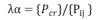
 ;式中:
;式中: —结构的自重荷载;
—结构的自重荷载;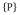 —结构的外加荷载;
—结构的外加荷载;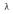 —荷载的加载系数。
—荷载的加载系数。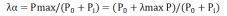 ;式中:
;式中: —表示结构承受的极限荷载;
—表示结构承受的极限荷载; —最大活载因子;p—表示基本活载;p1—表示设计活载。
—最大活载因子;p—表示基本活载;p1—表示设计活载。 。根据相关规范,在容许应力法计算时,要求1.7。按《公路斜拉桥设计规范》(JTGT3365-01—2020)中规定结构的安全系数4。一般情况下,进行非线性稳定分析时,稳定安全系数应满足上述要求。
。根据相关规范,在容许应力法计算时,要求1.7。按《公路斜拉桥设计规范》(JTGT3365-01—2020)中规定结构的安全系数4。一般情况下,进行非线性稳定分析时,稳定安全系数应满足上述要求。