旋转思想在初中数学解题中的妙用论文

　　摘要:旋转作为几何图形运动中的一个重要变换形式,是初中数学几何教学中的一项基本内容.图形通过旋转改变位置后重新组合,能够当作全等变换,不过需要在新旧图形之间找到变量与不变量,确定相关图形之间的关系,从而揭示出条件和结论的内在关联,找到解题的突破口.本文以旋转思想在初中数学解题中的妙用列举部分实例来说明.

 

　　关键词:旋转思想;数学解题;实际运用

 

　　在新时期教育背景下,初中数学教材内容的编排越来越注重同现实生活相接,课本中增添有图形变换的内容,包括旋转、翻折与平移等,其中旋转思想在几何解题中有着广泛的运用,也是近年来中考中经常出现的一个热点.在初中数学解题教学中,教师应指导学生根据题目实际情况巧妙运用旋转思想,降低试题的难题,使他们快速找到突破口,最终顺利解题.

 

 

　　在初中数学解题教学中,当运用旋转思想处理问题时,教师通常需从问题的结论与条件切入,引领学生从题干中提供的图形分析,分析题目的设计意图,在结合旋转变化过程中图形性状不发生改变的性质以及旋转角度发生变化的性质巧妙构图,让学生认真观察和分析图像的旋转变化确定解题思路,达到解答问题的目的.这样学生能够亲身经历图形旋转的过程,使他们通过解题训练进一步掌握图形旋转的性质,并深化对旋转思想的理解与应用.

 

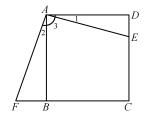
        例1如图1所示,四边形ABCD是一个正方形,三角形ADE经顺时针旋转后同三角形ABF重合,求(1)旋转中心是哪一点?三角形ADE旋转多少度?(3)假如把EF连接起来,那么三角形AEF是一个什么样的三角形?

图1

 

　　解析对于第(1)、(2)小题,学生通过观察能够直接得出答案,即为旋转中心是点A,三角形ADE旋转90°同三角形ABF重合;而对于第(3)小题,教师可先组织学生在小组内合作讨论与探究,结合已经学习过的数学知识思考:经常判断三角形的形状有直角三角形、等腰三角形与等边三角形,再结合图形旋转的性质很容易发现当EF连接起来以后,根据AE与AF相等、∠1与∠2相等能够得到∠EAF=∠2+∠3=90°,所以在三角形AEF中,AE=AF,∠∠EAF=90°,这充分说明三角形AEF是一个等腰直角三角形.

 

 

　　在处理数学问题时,进行合理猜想能够让题目显得更有活力与魅力,通过旋转思想的妙用融入到几何变式类的问题中,借此凸显出数学猜想的重要作用.要想培养学生的数学猜想能力,教师需坚持循序渐进的原则,借助一些变式训练,为学生进行猜想奠定良好基础,让他们学会从多个视角分析与解决问题.初中数学教师在解题训练中,可指导学生运用图形旋转思想进行巧妙猜想,把不同的图形关联起来,让他们进行观察、类比、猜想与验证.

 

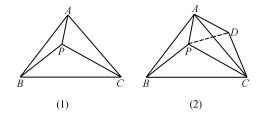
　　例2如图2(1)所示,三角形ABC是一个等腰直角三角形,其中AC=BC,四边形CDEF是一个正方形,连接BD、AF,(1)观察图形,猜想AF与BD之间的关系,且证明;(2)如果把正方形CDEF绕点C按顺时针方向旋转,使之一边落在三角形ABC内,请画出一个变换后的图形,并对照已知图形标记字母,分析题(1)中猜想的结论是否仍然成立?假如成立,直接写出结论,无需证明,如果不成立,说明理由.
 

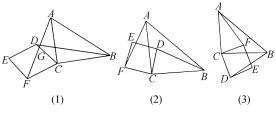图2

 

　　解析(1)让通过观察学生发现图中隐含着旋转变换,△ACF绕C点顺时针旋转90°,得到△BCD,由此猜想出AF=BD,且AF⊥BD.这样的猜想过程能为证明做铺垫,让学生顺利找到证明两个三角形全等的条件,得到△ACF≌△BCD,推出AF=BD与∠AFC=∠BDC,再利用∠AFC+∠FGC=

 

　　90°得到AF⊥BD.(2)图2(2)是CD边在△ABC内部时,图2(3)是CF边在△ABC内部时,当正方形CDEF绕点C旋转时,一边落在△ABC内部,始终有AF=BD数量关系与AF⊥BD的位置关系.

 

　　3采用图形旋转思想巧妙转化
 

 

 

　　在初中数学解题教学过程中,让学生“做一做,动一动”思维能够变得更加活跃,而遇到一些难以处理的几何图形类问题时,教师可以指导他们巧妙运用旋转思想,对题目中的图形或者图形的一部分进行旋转,由此找到解题的突破口.同时,初中数学教师应当提示学生紧紧抓住旋转后新图形和原图形所具备的性质,并依据特殊角的三角函数值、等腰三角形、等边三角形及正方形的性质等,让他们学会化繁为简,使其快速、准确的找到解题方法,

 

　　例3如图3所示,在三角形ABC中,AC与BC的长度一样,点D是边AB上的一点,求证:DB2+AD2=2CD2.

图3
 

 

　　解析处理旋转类的问题时要抓住两点:一是旋转后的图形与原图形全等,二是利用好旋转的角度.具体解答方法如下:学生利用旋转与转化的数学思想方法,把△ACD绕点C逆时针旋转90°,再把ED连接起来,这样将分散的线段DB、AD与CD整合到两个直角三角形△BDE和△CDE中,结合勾股定理能够得到ED2=DB2+BE2=DB2+AD2,继而得到ED2=CD2+CE2=2CD2.

 

 

　　在初中数学解题教学中,几何图形类题目占据着较大的比重,在平常训练与考试中均较为常见,而计算角度类问题属于基础性题型,处理这类题目时需要结合已知条件把分散的条件进行集中分析与处理.对此,初中数学教师可以引导学生巧妙应用旋转思想分析和解决角度问题,先对原图形进行旋转变化,分析图形的特殊位置和角度,再结合相关数学公式展开解题,使其把陌生问题转变成熟悉的问题,把复杂问题变得简单化,让他们轻松解题.

 

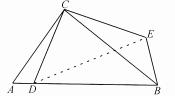
　　例4如图4(1)所示,点P是等边三角形ABC内的一点,其中PA的长度是3,PB的长度是4,PC的长度是5,求∠APB的大小.

 

　　解析当学生看到3、4、5在这组数据时,通常会第一时间想到勾股定理,这是直角三角形的三条边的长度,但是在本题中分散在三角形ABC内部,解题该题的关键是想法将这分散的三边集中到同一个三角形中,通过旋转转化实现.具体来说,可以让三角形APB围绕点A逆时针旋转60°后得到三角形ADC,把PD连接起来,如图4(2)所示,则AD=AP=3,DC=PB=4,∠PAD=60°,所以三角形PAD是一个等边三角形,则PD=PA=3,在三角形PDC中,PD2+DC2=32+42=52,PC2=52,由此得到∠PDC=90°,则∠APB=∠ADP+∠PDC=60°+90°=150°.

 

 

　　对初中数学解题教学而言,计算线段长度类问题也十分常见,这类题目从表面上看往往难度不大,但是仔细观察图形与分析题目内容以后,发现并不易求解,而且部分题目给出的条件较少,学生极易陷入到困境之中,他们很难快速形成准确的解题思路.因此,初中数学教师在具体的解题训练中,可以指导学生利用旋转思想对题目中的图形展开旋转与变换,明确旋转以后角、边的元素变化情况,使其形成清晰的解题思路,提高解题效率.

 

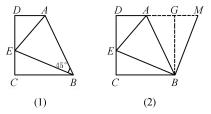
　　例5如图5(1)所示,在梯形ABCD中,AD∥BC,AD<BC,∠D是90°,BC与CD的长度一样,都是12,∠ABE是45°,AE的长度是10,那么CE的长度是多少?

 

　　图5

 

　　解析经过观察后发现将三角形BCE围绕点B顺时针旋转90°,就能够构成一个正方形,再结合三角形全等的性质确定边与边自己的关系.具体解题方法如下:把OA延长,使三角形BCE围绕点B顺时针旋转90°,同DA的延长线分别相交于点G与点M,如图5(2)所示,得出一个正方形BCGDG,则BC=BG,又因为∠CBE=∠GBM,所以Rt△BEC≌Rt△BMG BM=BE∠ABE=∠ABM=45°△ABE≌△ABM,AM=AE=10,此时,设CE=x,则AG=10-x,AD=12-(10-x)=2+x,DE=12-x,那么在Rt△ADE中,AE2=AD2+DE2,即102=(x+2)2+(12-x)2,化简后得到x2-10x+24=0,解之得x1=4,x2=6,即为CE的长是4或者6.

 

 

　　[1]吴艳华.关于图形旋转变换专题的解题方法探究[J].数理化解题研究,2021(29):48+60.

 

　　[2]周鸣.图形的旋转在中考中的运用与思考[J].数学学习与研究,2021(28):140-143.

 

　　[3]宋景华.例谈初中数学解题训练教学[J].数理化解题研究,2020(02):14-15.

 

　　[4]贺群.初中数学解题能力巧提升—旋转中的不变性问题[J].学苑教育,2020(05):52.