SCI论文(www.lunwensci.com):
摘要:在一些与平面几何相关的求值问题中,经常借助相似三角形的构造、判定与性质等的应用,而让问题合理转化、直观形象,能有效解决计数、线段、比值、面积以及综合应用等相关问题的求值,利用相似三角形引领并指导数学教学与研究.
关键词:相似三角形;计数;线段;比值;面积
相似三角形是在初中平面几何中一个非常重要的内容,包括相似三角形的定义、判定、性质等,同时涉及特殊的直角三角形相似的判定及直角三角形的射影定理,是平面几何的重要知识点与考点之一.在破解一些相关的平面几何求解问题中,巧妙借助相似三角形的相关知识来处理,经常可以合理转化,化难为易,出奇制胜.以下结合几类常见的相似三角形中的求值问题,如计数、长度、比值、面积以及综合应用等相关的求值题加以剖析.
1计数问题
例1如图1所示,在△ABC中,ED∥AB,FG∥AC,PH∥BC,相应的交点分别为A1、B1、C1,则图中与△ABC相似的三角形的个数为__个.
分析根据相似三角形的性质,要判断图中与△ABC相似的三角形,可以从平行这个条件出发,找到对应相等的角,从而得以确定两三角形相似.
解析由于PH∥BC,那么∠APH=∠B,而∠A是公共角,则△APH∽△ABC,同理可以判断△BGF∽△ABC,△CED∽△ABC,进一步,FG∥AC,那么∠PFC1=∠A,又∠FPC1=∠B,△FPC1∽△ABC,同理可以判断△DGA1∽△ABC,△HEB1∽△ABC,而ED∥AB,那么∠FPC1=∠A1 B1 C1,而∠FPC1=∠B,则∠A1 B1 C1=∠B,同理可得∠A1 C1 B1=∠C,则△A1 B1 C1∽△ABC,所以图中与△ABC相似的三角形的个数共有7个,故填答案:7.
点评三角形相似的判定关键是结合三角形相似的性质加以分析,在求解三角形相似的问题的过程中,往往是在熟练掌握相应性质的基础上,结合直观图形加以正确分析.
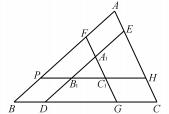
图1
2长度问题
例2如图2,正方形ABCD的边长是2,BE=CE,MN=1,线段MN的两端在CD、AD上滑动,当DM=__时,△ABE与△DMN相似.
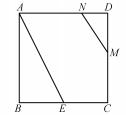 图2
图2
分析因为两个三角形都是直角三角形,当且仅当两直角边之比相等时它们相似,据此可列一个方程,再结合MN=1列方程组,解此方程组得DM的值.
解析要使△ABE∽△DMN,而这两个三角形都是直角三角形,依题意,可得
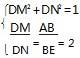
或
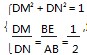
,解得DM=

或

.
故填答案:
 或
或
点评本题是探求两个三角形相似的条件问题,实质是以三角形相似为条件,求线段长度问题,关键是找到相应的比值并结合相关条件加以求解.特别在实际求解时,要全面考虑,比如本例中就容易忽视其中的一种情形.
3比值问题
例3如图3所示,AB和BC分别与圆O相切于点D,C,AC经过圆心O,且BC=2OC,则

=
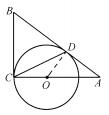 图3
图3
分析通过作出辅助线OD,根据两直角三角形△ADO与△ACB相似来建立关系式,结合题目条件来证明对应的等式成立.
证明连接OD,因为AB和BC分别与圆O相切于点D,C,所以∠ADO=∠ACB=90°,又因为∠A=∠A,所以Rt△ADO∽Rt△ACB,所以

=

,又BC=2OC=2OD,故AC=2AD,即

=2.
故填答案:2.
点评结合辅助线的构造,利用直角三角形的相似以及相关条件加以确定相关的求值问题.对于平面几何中的求值问题,关键是正确引入相关的辅助线,加结合相应条件的变换与转移,从而达到求值的目的.
4面积问题
例4如图4所示,在四边形ABCD中,E是AB上一点,EC∥AD,DE∥BC,若S△BEC=1,S△ADE=3,则S△CDE的值为
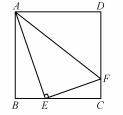 图4
图4
分析根据平行线的性质转化三角形的面积比为对应的线段比,结合平行线所确定的角的关系证明△BEC∽△EAD,再由比例性质转化为面积之间的比值即可求解S△CDE的值.
解析由于EC∥AD,可得S△DCE∶S△ADE=EC∶AD,而DE∥BC,则有S△BCE∶S△CDE=BC∶ED,又因为∠ECB=∠DEC=∠ADE,∠BEC=∠EAD,所以△BEC∽△EAD,可得EC∶AD=BC∶ED,即S△DCE∶S△ADE=S△BCE∶S△CDE,解得S△CDE=3.
故填答案:3.
点评通过平行线的性质,结合相似三角形中的对应边的比例关系与相应的三角形的面积的比例关系的转化与应用来分析与处理问题.
5综合应用问题
例5如图5,已知正方形ABCD的边长为4,E是BC上的点,EF⊥AE交CD于F.试猜想:点E在什么位置时,△ADF的面积最小?最小面积是多少?并证明你的结论.
分析要猜想对应点的位置,关键是结合相应的几何图形与关系式加以分析判断,巧妙引入未知数,通过建立有关面积的函数关系式,利用函数的最值问题来判断对应的几何问题.
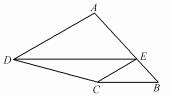 图5
图5
解析当点E是BC的中点时,△ADF的面积最小,最小面积是6.
下面证明以上猜想的结论:
设BE=x,那么EC=4-x,
由于四边形ABCD是正方形,∠AEF=90°,则△ABE∽△ECF,可得
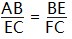
.
即
 =
=
,则FC=x-

x
2,
可得
DF=DC-FC=4-(x-

x2)=4-x+

x2
所以S△ADF=

AD·DF
=

×4(4-x+x2)
=

x2-2x+8
=

(x-2)2+6,
故当x=2时,即E是BC的中点时,△ADF的面积最小,最小面积是6.
点评在平面几何问题中,往往可以有机地结合相应的函数等相关问题,利用函数等相关问题的性质来处理与解决对应的平面几何问题,这是一种非常巧妙与有效的办法.关键是将平面几何问题进行代数化,并加以正确的分析与判断.
相似三角形及其应用是在初中平面几何的基础知识上的进一步拓展与提升,特别是在一些平面几何的求值问题中,合理借助辅助线与相似三角形的构造,通过对判定、性质等一系列的转化与应用,有效培养学生逻辑推理能力、图形直观能力与创造思维能力,其也是历年中考数学命题中的一大热点问题,应该引起一线教师高度重视.
参考文献:
[1]田传弟.妙用拼图法求tan15°的值[J].初中数学教与学,2020(01):12-14.
[2]王锋.平行“牵”相似求值如添“翼”[J].中学生数理化(初中版·中考版),2020(Z1):9-11.
[3]郑泉水.构造相似三角形解中考题一例[J].数理化学习(初中版),2016(03):10+12.
关注SCI论文创作发表,寻求SCI论文修改润色、SCI论文代发表等服务支撑,请锁定SCI论文网!
文章出自SCI论文网转载请注明出处:https://www.lunwensci.com/ligonglunwen/40836.html



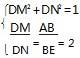 或
或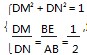 ,解得DM=
,解得DM= 或
或 .
. 或
或
 =
=
 =
= ,又BC=2OC=2OD,故AC=2AD,即
,又BC=2OC=2OD,故AC=2AD,即 =2.
=2.

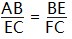 .
. =
= ,则FC=x-
,则FC=x- x2,
x2, x2)=4-x+
x2)=4-x+ x2
x2 AD·DF
AD·DF ×4(4-x+x2)
×4(4-x+x2) x2-2x+8
x2-2x+8 (x-2)2+6,
(x-2)2+6,
