浅析初中数学解题中隐含条件的应用论文

SCI论文（www.lunwensci.com）:
 

　　摘 要 : 隐含条件是指没有明确给出 ,但能从已知条件中推出的条件. 初中数学解题中注重隐 含条件的挖掘与应用 ,能尽快地找到解题思路 , 实现解题能力的提升. 因此 ,初中数学解题教学中为 使学生认识到隐含条件的重要性 ,掌握相关的应用技巧 ,应结合具体例题为学生展示隐含条件的具体应用过程.

　　关键词 :初中数学 ;解题;隐含条件 ;应用

　　中数学习题灵活多变 ,隐含条件多种多样. 部分 隐含条件决定着学生能否顺利、正确地解答出相关 习题 ,重要性不言而喻 , 因此教学中既要通过理论知 识的讲解使学生关注解题中的隐含条件 ,又要为学 生展示如何运用隐含条件进行解题. 本文结合根式 类习题、绝对值类习题、圆类习题、函数类习题、方程 类习题、因数分解类习题、三角形类习题 ,展示隐含 条件在解题中的应用 ,以供参考.

 

　　1 用于解答根式类的习题

　　二次根式是初中数学的重要知识点. 围绕二次 根式设计的习题 ,往往不明确告知被开方部分应大 于等于零. 解答该类习题应注重利用这一隐含条件 , 以迅速找到解题突破口.

　　例 1 已 知 实 数 a 满 足 += a ,则 a - 20082 的值为( ) .

　　A. 0 B. 1 C. 2008 D. 2009

　　很多学生看到题目中涉及的数字较大 , 心中有所畏惧 , 一 时 不 知 道 如 何 作 答. 事 实 上 该 类 题 主要考查学生思维的灵活性 ,计算量 一 般不会太 大. 解题 的 关 键 在 于 充 分 利 用 题 干 中 的 隐 含 条 件 , 即 ,a - 2009 ≥0 .

　　因为+= a , 所 以 |2008 - a | += a

　　要想根式有意义 ,应满足 a - 2009 ≥ 0 , 即 a ≥ 2009 , 因此 ,2008 - a < 0

　　即 a - 2008 + = a ,= 2008 ,a - 2009 = 20082 ,得 a - 20082 = a - ( a - 209 )= 2009 ,于是选择 D 项.

　　2 用于解答绝对值类的习题

　　绝对值是初中数学的重点知识. 其中去绝对值 是初中数学的难点 ,存在“ 去绝对值后的结果为非 负”这一隐含条件. 解题中注重这一 隐含条件的应 用 ,可获得事半功倍的解题效果.

　　例 2 已知( a + b )2 + | b + 5 | = b + 5 ,且 | 2a - b- 1 | = 0 ,则 ab 的值为( ) .

　　A. -    B.    C. -      D.

　　本题中涉及平方、绝对值等知识 ,具有一定的技 巧. 解题的关键在于能够充分挖掘隐含条件 ,将绝对 值去掉 ,找到参数 a、b 之间的关系 ,而后运用已知条 件求出参数的值.

　　因为( a + b )2 + | b + 5 | = b + 5 ,且 ( a + b )2 ≥0 , | b + 5 | ≥0 ,则两者之和一定是大于等于零的数

　　所以 b + 5≥0 ,所以( a + b )2 + b + 5 = b + 5 , a + b = 0 ,即 a = - b

　　又因为 | 2a - b - 1 | = 0 ,即 , | 3a - 1 | = 0 ,即 ,a = ,b = - ,即 ,ab = -,选择 C 项.

　　3 用于解答圆类的习题

　　圆是初中数学的重点、难点知识 ,题型复杂多 变. 部分习题仅仅给出文字描述 ,而满足文字情境的 情况不止一种 , 因此 ,解题中应通过画相关草图 ,运 用所学知识 ,找到隐含的情境 ,逐一 的分析解答 ,保 证考虑问题的全面性 ,才能得全分.

　　例 3 已知点 A ,C 是半径为 3 的圆周上两点 , 点 B 为弧 AC 的中点 ,以线段 BA、BC 为邻边作菱形 ABCD ,顶点 D 恰在该圆直径的三等分点上 ,则该菱形的边长为( ) .

　　A.5 或 2 2

　　B. 5 或 2 3

　　C. 6 或 2 2

　　D.6 或 2 3

　　该题目难度并不大 ,但设计有陷阱 ,解题时需认 真审题 ,找到其隐含条件 ,再进行解答 ,即 ,满足题干 条件的菱形存在两种可能. 因题目中未给出 D 时在 直径的三分之一处还是三分之二处 , 因此 ,需进行分 类讨论.

　　①当点 D 处在直径的三分之一处时 ,如图 1 所示 ,根据已知条件可知 BD =× 6 = 2 ,且 DE = BE = 1 ,又因为 OB = 3 ,则 OE = OB - BE = 3 - 1 = 2 ,所以 EC =OC2 - OE2 = 5 ,所以 BC = BE2 + EC2 =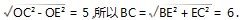

　　②当点 D 处在直径的三分之二处时 ,如图 2 所示 ,根据已知条件可知 BD = × 6 = 4 ,且 DE = BE= 2 ,又因为 OB = 3 ,则 OD = BD - OB = 4 - 3 = 1 ,则 OE = DE - OD = 2 - 1 = 1 ,所以 EC = = 2 2 ,所以 BC = = 2 3 . 综上可知 ,菱形 的边长为 6 或 2 3 ,选择 D 项.

　　4 用于解答函数类的习题

　　二次函数涉及很多知识点 ,尤其部分习题对学 生的理解以及分析问题的能力要求较高. 为提高解 题正确率 ,应先认真审题 ,尤其对于带有图形的习 题 ,更应注重观察图像 ,充分挖掘、灵活应用隐含在 图像中的隐含条件.

　　例 4 如图 3 , 已知二次函数 y = ax2 + bx + c 的 图像经过点 A、B、C 三点 ,设 C 的纵坐标为 y1 ,若点 D (x2 ,y2 ) 为抛物线上任意一点 ,则一些结论中 : ① 二次函数 y = ax2 + bx + c 的最小值为 - 4a;②若 - 1 ≤x2 ≤4 ,则 0 ≤y2 ≤5a;③若 y2 > y1 ,则 x2 > 4 ;④ 一元二次方程 cx2 + bx + a = 0 的两个根据为 - 1 和 1则正确结论的个数为( ) .

       

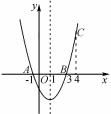
　         　图 3

　　A. 1 B. 2 C. 3 D. 4

　　题目结合二次函数进行设问 ,一些条件并未直 接给出 ,而是展示在了图像中 ,要求学生充分运用隐 含条件才能做出正确地判断. 根据图像可挖掘出以 下隐含条件:a > 0;图像过( - 1 ,0 ) , (3 ,0) 两点 , 即 , 函数可改写成 y = a (x + 1 ) (x - 3 ) ; 函数的对称轴 x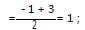

　　对于①将 x = 1 代入函数表达式可得其最小值 为 - 4a ,正确 ;

　　对于② - 1 ≤x2 ≤4 , 当 x2 = 4 时 ,y2 取得最大值= a × (4 + 1 ) × (4 - 3 ) = 5a , 因此 , - 4a ≤y2 ≤5a , 错误 ;

　　对于③若 y2 > y1 , 由图可知 x2 > 4 或 x2 < - 2 , 错误 ;

　　对于④因为 y = ax2 + bx + c = a (x + 1 ) (x - 3 )= ax2 - 2ax - 3a ,则 b = - 2a ,c = 3a ,将其代入 cx2 + bx + a = 0 中 ,得到 - 3ax2 - 2ax + a = 0 ,又 a≠0 ,则 3x2 + 2x - 1 = 0 ,解得 x1 = - 1 ,x2 =,正确.

　　综上只有①和④两个结论正确 ,选择 B 项.

　　5 用于解答方程类的习题

　　在初中阶段学习到的方程主要有一元一 次方 程 ,二元一次方程 ,一元二次方程等. 部分习题在描 述方程时并未直接给出方程的具体形式 ,解答时需 要根据其描述以及所学知识 ,充分挖掘隐含条件 ,认 真、细致地考虑每一种可能的情况. 同时 ,还应做好对 要求解问题的转化 ,利用根与系数的关系进行分析.

　　例 5 已知关于 x 的方程 ax2 + ( a + 2 )x + 9a =0 有两个不等实数根 x1 ,x2 ,且 x1 < 1 < x2 ,则 a 的取 值范围是( ) .

　　A. - < a <              B. a >

　　C. a < -                       D. - < a < 0

　　该题虽然未指明方程的类型 ,但是其指出方程“ 有两个不等实数根”, 因此可知其属于一元二次方 程. 解题是需要考虑一元二次方程成立的条件 , 即 , 二次项系数不能为零. 同时 ,对“x1 < 1 < x2 ”这一条 件进行转化 ,利用根与系数的关系不难作答. 因为关 于 x 的方程 ax2 + ( a + 2)x + 9a = 0 有两个不等实数 根 x1 ,x2 ,所以 a≠0 ,Δ = ( a + 2 )² - 4a × 9a > 0 ,解得 - < a <,又因为两个不等实数根 x1 ,x2 满足 x1 < 1 < x2 ,所以(x1 - 1 ) (x2 - 1 ) < 0 , 即 ,x1 x2 - (x1 + x2 ) + 1 < 0 ,x1 + x2 =-,x1 x2 = 9 , 即 ,9 + + 1 < 0 ,解得 - < a < 0. 综上分析可知 ,a 的取值范 围为 - < a < 0 ,选择 D 项.
 

 

 

　　教学实践实践表明 ,初中数学解题中学生不注 重隐含条件的应用 ,要么一时难以找到解题思路 ,要 么得出的结果不正确、不全面. 因此 ,在教学中为了 提高学生的解题正确率以及解题能力 ,应注重为学 生讲解隐含条件的应用 ,使学生掌握不同题型的解 题规律、技巧. 同时 ,多组织学生开展相关的解题训 练活动 ,使学生经历犯错、纠错过程 ,积累隐含条件 的应用技巧.

　　参考文献 :

　　[ 1 ] 李惠娟. 初中数学解题中隐含条件及应用分析 [J ] . 课程教育研究 ,2020( 19) :143 - 144 .

　　[2 ] 陈文榜. 初中数学解题教学中隐含条件的应用 [J ] . 数学大世界(上旬) ,2020(01) :74 .

　　[3 ] 张爱群. 初中数学解题中隐含条件的挖掘策略 [J ]. 数理化学习(初中版) ,2018(12) :6 - 7 + 10.

　　[4 ] 施晴花. 探讨初中数学解题教学中隐含条件的 应用[J ] . 数学大世界(上旬) ,2018(09) :68 .

　　[5 ] 王志军. 发掘隐含条件 助力数学解题—初 中数学解题教学中隐含条件的应用[ J ] . 数理 化解题研究 ,2021(32) :6 - 7 .

 
关注SCI论文创作发表，寻求SCI论文修改润色、SCI论文代发表等服务支撑，请锁定SCI论文网！
 

文章出自SCI论文网转载请注明出处：https://www.lunwensci.com/ligonglunwen/40488.html