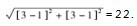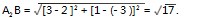SCI论文(www.lunwensci.com):
摘要:初中数学教学中“饮马问题”的题型既是常考题,又是初中数学教学一个很难突破的知识点,学生遇到这类的题目,往往找不到解决问题的突破口,不懂得对知识进行迁移、应用.在教学中需给学生灌输一个思想:求直线上一点到直线同侧两点的连线段长度之和的最小值问题就是”饮马问题“,解决这类问题的关键依据是:“两点之间线段最短”或是“三角形任意两边之和大于第三边”.
关键词:饮马问题;数形结合;对称求值
古希腊亚里山大里亚城里,有一位将军从A地出发到河边饮马,然后回到同一河岸边的B地军营视察,问他应该怎样走距离才最短?这类问题在数学教学中都称为“将军饮马问题”.在北师大版初中数学七年下册第123页第5题有一个典型的饮马问题:如图1所示,在一条街道的同侧有A、B为居民区,某一天小明要从居民区A出发,先到街道旁一井边打水,送到居民区B.请你帮他确定最短路线?有关饮马问题的解决关键是找出表示“河流”所在的直线,再找出其中点A或B的对称点,属于动态几何问题.我们对北师大版初中数学七年下册第123页第5题进行分析,街道就是“河流”所在的直线,点A关于“河流”的对称点为A′,连结A′B,交街道于点P,则AP+BP=A′P+BP=A′B.则A′B就是所求的最短线段.
本题实质上是求“两点之间线段最短”.它考查的是两点之间线段最短,是应用较为灵活的题型,从最为简单的直接考查两线段之和最小,推广到以三角形、四边形、特殊四边形、圆、一次函数、二次函数为背景的相关题目.初中数学教学中“饮马问题”的题型出现多次,它一直是初中数学教学一个很难突破的知识点,学生遇到这类的题目,往往找不到解决问题的突破口,不懂得对知识进行迁移、应用.因此,在教学中需给学生贯灌输一个思想:求直线上一点到直线同侧两点的连线段长度之和的最小值问题就是”饮马问题“,解决这类问题的关键依据是:“两点之间线段最短”或是“三角形任意两边之和大于第三边”.

图1
下面由这一知识点演绎出来的相关题型进行归类,提出自己的见解.
1把饮马问题这个模型放在圆中,利用圆的直径作为“河流”来创建题目.
例1如图2,AB是☉O的直径,AB=a点M在☉O上,∠MAB=20°,N是弧MB的中点,P是直径AB上的一动点,若MN=b,则△MNP周长的最小值是多少?

图2
分析在解决这一题目时要教会学生抓住本题的实质是一个饮马问题,MN两点在直径AB同侧.因此只要作出N关于AB的对称点N′连结MN′,交
AB于P,则△MNP周长的最小值是PM+PN+MN=PM+PN′+MN=MN+MN′=M+N′弦NM的长.求弦MN′的长就必须用到直径a和弦MN′所对圆心∠MON′∠MON′=∠MOB+∠N′OB=40°+20°=60°又OM=ON′,因为△MON′是等边三角形因此弦MN′= (半径)则△MNP周长的最小值为b+
(半径)则△MNP周长的最小值为b+ .
.
例2如果对上一题目稍加改动,如上图将∠MAB=20°,改为∠MAB=30°,其它条件不变,又可以产生一题目.抓住题目的实质直径AB相当于河流,M、N为同侧两点.这一题目是饮马问题,MN′所对圆心∠MON′=60°+30°=90°又OM=ON′,
所以△MON′是等腰直角三角形,因此弦MN′= ,△MNP周长的最小值为b+
,△MNP周长的最小值为b+ .
.
2把这个模型放在多边形中,以三角形或特殊四边形为背景,利用特殊三角的对称轴作为“河流”或特殊四边形的对角线为“河流”来设计题目
例3如图3在正△ABC中,AB=6,AD⊥BC垂足为点D,点E、F分别为AD、AB上的动点,则BE+FE的最小值是多少?

图3
分析本题还是在直线AD上找出一点到同侧两点B、F的距离之和最小,一看就是一饮马问题上.关键在于找出点B、F其中一点的对称点,而点B、C关于直线AD对称.因此只要过C作CF垂直于AB垂足为F,CF交AD于点E,则BE+FE=CE+FE=CF此时BE+FE就是求一等边三角形的高.(6sin 30°=3 3)
解因为点B、C关于直线AD对称,所以过C作CF垂直于AB垂足为F,所以BE+FE=CE+FE=CF最小,此时BE+FE就是此等边三角形的高CF,所以CF=6sin 30°=3 3.
3把这个模型放在平面直角坐标系中,利用x轴,y轴,抛物线对称轴或某一直线为“河流”来设计求最小值的问题.
例4若f(m)=
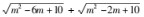
,求当m为何值时,f(m)有最小值,且f(m)的最小值是多少?
我们若对公式进行如下处理
到此我们可以得知:本题目是在x轴上求一点(m,0)到A点(3,1)B(1,3)的距离之和最小,又是一个饮马问题把x轴当成河流,A点(3,1)B(1,3)是河流同侧的两点.如些一转化它是一个容易题了.具体解法如下:
例5将上题改为:如图4,在平面直角坐标系中,已知A(1,3)、B(3,-1),若要在x轴上找一点P,使|AP-BP|最大,则点P的坐标为多少,|AP-BP|最大值是多少?
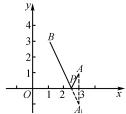
图4
解析我们在上面求解中大多数都求最小值问题很少出现最大值,而本题是求最大值,它还是转化
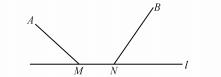
为两点间距离的问题,点B(3,-1)关于x轴的对称点B1(3,1),连接A B1并延长交x轴于P,求出直线A B1为y=-2x+5,直线y=-2x+5,与轴的交点 P(- ,0),|AP-BP|最大就是|AB|=
,0),|AP-BP|最大就是|AB|=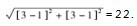
例6如图5.已知A(1,3),B(3,1),MN=1且MN是x轴上的一动线段,则AM+BN的最小值是多少?
图5
这是一个相对隐蔽的饮马问题,因为还是直线同旁的两条线段之和的问题,而饮马问题是在河流上找一点P,这一问题是一线段MN,能否将线段转化为点,A点向左(右)平移AA1=MN(使A、B两点靠近,缩短A、B两点间的距离)作A1关于x轴的对称点A2连接则A2 B,那么AM+BN=A1 N+BN=A2 N+BN=A2 B.
利用这种方法解答上述题目,A点向右平移MN(1个单位)得A1(2,3),A1关于x轴对称点A2(2,-3),连接A2 B,则A2 B=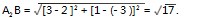
数学来源于生活,我们学习数学的目的是学会应用数学知识解决实际问题.饮马问题在日常生活中经常遇到,怎样节省材料降低成本需求最小值,这对于我们构建环境友好型、资源节约型的美丽中国有着重要的意义.
参考文献:
[1]苏国东.例谈用“相似法”破解将军饮马问题[J].中学数学,2021(10):78-79+89.
[2]张金凤.“将军饮马问题(第二课时)”教学设计[J].中学课程资源,2021,17(08):35-40.
[3]覃秀敏,刘运龙,张金江.从“将军饮马问题”谈模型思想的渗透[J].中学教学参考,2021(02):29-30.
关注SCI论文创作发表,寻求SCI论文修改润色、SCI论文代发表等服务支撑,请锁定SCI论文网!
文章出自SCI论文网转载请注明出处:https://www.lunwensci.com/ligonglunwen/39891.html



 (半径)则△MNP周长的最小值为b+
(半径)则△MNP周长的最小值为b+ .
. ∠BOM=20°,所以∠MON′=∠MOB+∠N′OB=40°+20°=60°,又OM=ON′,所以△MON′是等边三角形,所以弦MN′=
∠BOM=20°,所以∠MON′=∠MOB+∠N′OB=40°+20°=60°,又OM=ON′,所以△MON′是等边三角形,所以弦MN′= ,△MNP周长的最小值是PM+PN+MN=PM+PN′+MN=MN+MN′=b+
,△MNP周长的最小值是PM+PN+MN=PM+PN′+MN=MN+MN′=b+ .
. ,△MNP周长的最小值为b+
,△MNP周长的最小值为b+ .
. ∠BOM=30°,所以∠MON′=∠MOB+∠N′OB=60°+30°=90°,又OM=ON′,因为△MON′是等腰直角三角形,所以弦MN′=
∠BOM=30°,所以∠MON′=∠MOB+∠N′OB=60°+30°=90°,又OM=ON′,因为△MON′是等腰直角三角形,所以弦MN′= △MNP周长的最小值是PM+PN+MN=PM+PN′+MN=MN+MN′=b+
△MNP周长的最小值是PM+PN+MN=PM+PN′+MN=MN+MN′=b+ .
.
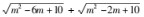 ,求当m为何值时,f(m)有最小值,且f(m)的最小值是多少?
,求当m为何值时,f(m)有最小值,且f(m)的最小值是多少?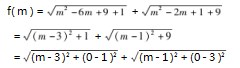
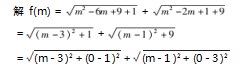
 ,所以与轴交点P(,0)A1 B=
,所以与轴交点P(,0)A1 B=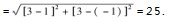

 ,0),|AP-BP|最大就是|AB|=
,0),|AP-BP|最大就是|AB|=