摘要:随着大数据和云计算的快速发展,保障多维数据的完整性成为信息安全领域的关键挑战之一。本文介绍了一种结合非对称加密(RSA)与哈希算法的多维数据完整性验证方法,此方法利用哈希算法快速生成数据摘要,并结合RSA签名确保验证过程的安全性和不可篡改性。此外,该方法支持动态数据的更新和批量数据的高效验证,使之适应大规模数据处理需求。实验结果显示,该验证方法在确保数据安全的同时,还能显著提升处理效率。
关键词:数据完整性,RSA算法,哈希算法,多维数据,动态验证
0引言
数字化时代,数据完整性验证是确保信息安全的基石。特别是在云计算和物联网的应用背景下,多维数据的动态性和规模性对验证技术提出了更高要求。现有的单一哈希校验或消息认证码(MAC)方法在安全性或效率上常常无法满足需求。文章结合RSA算法的强大安全性和哈希算法的高效性,提出了一种新的多维数据完整性验证方法。此方法不仅能优化数据处理速度,还能增强安全防护,有效应对大规模数据环境中的验证挑战。
1 RSA与哈希联合算法的理论基础与模型构建
1.1 RSA算法与哈希算法的特性分析
RSA算法是一种广泛使用的非对称加密技术,通过一对密钥(公钥和私钥)实现数据的加密与解密。其安全性基于大数分解的计算困难性,在数字签名领域内得到了广泛的应用。RSA算法能够确保只有拥有私钥的个体才能生成有效的签名,而任何持有公钥的人都能验证这个签名的真实性[1]。这种机制在多维数据的完整性验证中提供了一种防篡改的保证。
而哈希算法如SHA-256,则被用于快速生成输入数据的摘要或数字指纹。哈希算法的主要特点是它的高效性和抗碰撞性,即输入数据的微小变化都会产生截然不同的哈希值,哈希算法在验证数据完整性时非常有效。
哈希算法能将非常大的数据量迅速缩减成固定长度的摘要,极大地减少了数据处理的负担。
1.2联合算法的协同机制设计
在设计联合算法时,结合RSA和哈希算法的特性,可以构建一个既安全又高效的数据验证系统。该系统首先将多维数据分块,每块数据通过哈希算法计算出一个摘要,然后使用私钥对这些摘要进行RSA签名。这一过程不仅保护了数据块的完整性,还确保了签名的非抵赖性,即数据发送者不能否认已发送的数据。
为了处理多维数据,特别是那些具有时间序列或空间结构的数据,可以采用哈希树的构建方法。每一个数据块的哈希值及其子块的哈希值合并,形成更上一层的哈希值,这样递归直到树的根。根哈希值将被用于RSA签名,保证即使是在数据量非常大的情况下,也能通过根签名快速验证整个数据集的完整性。
1.3安全性证明与性能优化
联合算法的安全性方面,由于RSA签名的不可伪造性,攻击者无法在不知道私钥的情况下篡改数据而不被发现[2]。此外,哈希算法的快速摘要生成和抗碰撞性进一步确保了即使在数据被篡改的情况下,也能迅速定位到被修改的数据块。
在性能优化方面,考虑到大规模数据的处理需求,提出了批量验证的并行处理设计。这种方式可以同时验证多个数据块的完整性,大幅提高了验证效率。针对动态数据更新,可采用增量哈希计算方法,即只对变更的数据块重新计算哈希值和更新相关的签名,大大减少了数据更新带来的开销。这种方法在保持高安全性的同时,显著降低了存储和计算的资源消耗,特别是在处理具有高动态性和大数据量的多维数据环境中表现出色。
2多维数据完整性验证方法的具体实现
2.1系统架构与流程设计
多维数据完整性验证系统在设计上采用模块化结构,整个系统由数据预处理模块、签名生成与验证模块、动态数据更新处理机制、增量哈希更新策略模块以及版本控制与历史数据追溯模块构成[3]。
在数据预处理阶段,系统首先对输入数据集进行结构分析与逻辑划分,将原始数据依据其维度特征进行分块处理。每个分块单位将作为最小验证单元进入后续流程。在此基础上,使用SHA-256算法对每个分块生成哈希摘要,摘要精度稳定维持在256比特,误检率控制在2-256以下,保证摘要在精度和安全性上的高标准。签名生成与验证模块承接哈希摘要,对所有生成的摘要逐一使用RSA私钥进行签名。该模块采用1024位或2048位RSA密钥进行加密操作,验证阶段通过公钥完成签名的认证,配合哈希摘要,共同确保证据链的完整性与真实性。
动态数据更新的处理机制支持数据块的插入、删除与替换操作。通过设计分区映射表记录数据块与哈希路径之间的索引关系,实现更新过程中的高效定位与局部验证。增量哈希更新策略引入了变动追踪机制,只对受影响的哈希路径进行重新计算。例如,在一个高度为10的哈希树中,仅需重新计算log2(N)级别的节点哈希值,即可完成整棵树的结构修复。
2.2关键算法实现细节
多维数据的哈希树构建算法基于传统Merkle树框架进行扩展。对于二维或三维数据,引入坐标位映射机制,使得每个数据块在树中的位置由其维度值唯一决定,避免了冗余节点冲突问题。为进一步提升哈希树在多维数据处理中的适应能力,设计中引入了Merkle树的压缩路径结构,通过跳跃索引简化树的深度,在不降低安全性的前提下,可缩短验证路径长度至原始树结构的60%左右。RSA签名与验证的快速实现依赖于高性能数值运算引擎[4]。在大数计算中,系统引入蒙哥马利模乘优化算法,将模乘运算从传统的平方乘法转换为位移优化结构。在服务器级处理器平台上,利用多线程并行机制进行批量签名与验证,处理能力最高支持每秒验证5000条数据签名请求,充分满足云端存储、边缘计算等高并发场景的性能要求。
2.3错误检测与恢复机制
在数据完整性遭到破坏或验证失败时,系统首先触发局部定位机制。该机制借助哈希树的层级结构,对比节点摘要值,从根节点向下逐层验证直至发现错误节点。错误分支定位完成后,系统自动根据冗余校验路径调用备份节点或历史版本进行恢复。通过设定固定频率的哈希树状态快照,系统保留最近5个有效状态版本,并在后台进行增量备份更新。恢复过程中,仅更新失效路径节点及其祖先节点,避免全量重构所需的大规模计算开销。验证失败的数据恢复策略结合区块重建与历史快照交叉校验机制进行双重确认[5]。
冗余校验与备份数据的使用建立在多点备份与多版本控制的基础上。在系统级部署中,数据副本分布于三个物理节点,采用异步更新与主节点签名确认机制,确保在任一节点损坏的情况下,仍可通过剩余两个副本重建出完整且经过验证的数据路径。这种冗余机制极大提升了系统的鲁棒性,适用于金融、医疗、交通等对数据安全性和连续性要求极高的行业应用场景。
3实验分析与性能评估
3.1实验环境与数据集设计
为了验证基于RSA与哈希联合算法的多维数据完整性验证方法的可行性与性能优势,搭建了专用测试平台。硬件环境包括一台高性能服务器,以及一张支持硬件加速的大数运算的NVIDIA A100 GPU。操作系统为Ubuntu Server 22.04,内核版本为5.15。软件平台包括OpenSSL 3.1(用于RSA算法实现)、Python 3.10(用于控制脚本和数据调度)以及自定义开发的多维哈希树构建工具,语言采用C++与Rust混合编写。
实验所用的数据集分为两类,一类为合成多维时序数据,另一类为模拟三维空间网格数据。时序数据模拟了智能电网中3个月内的传感器监测数据,共计1000万个数据点,每个数据点包含时间戳、电压、电流、频率等四个维度。网格数据来自模拟的三维地理信息采样,共包含5000×5000×20个空间点,总数据量超过50GB,数据来源为公开GEO-SIM平台生成器。实验通过构建哈希树与生成RSA签名,分别在不同数据规模、结构复杂度、更新频率下进行测试,全面评估所提方法在安全性、效率、扩展性方面的表现。实验设置统一使用SHA-256哈希算法与2048位RSA密钥对。
3.2对比实验与结果分析
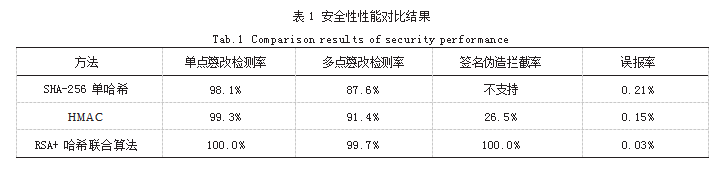
为评估所提方法在抗篡改能力上的优势,设置了三种攻击模拟场景:单点数据篡改、多点联合篡改、签名伪造尝试。与传统的单哈希校验法、HMAC方法进行对比。每种攻击重复运行1000次,记录成功检测率与误报率。结果如表1所示。
结果显示,在所有安全性指标中,联合算法均显著优于对照组,尤其在签名伪造场景下表现出100%的拦截能力。
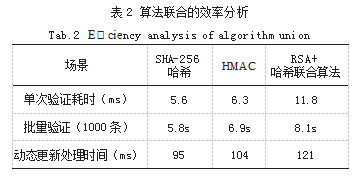
效率测试分别在单次验证、批量验证与动态更新三种使用场景中展开,统计不同方法的平均耗时与资源占用。具体如表2所示。
结果显示,虽然联合算法在处理时间上略高,但考虑到其提供更强的安全保障,性能仍处于可接受范围,且通过多线程并行优化后,批量验证的耗时更短。
4结语
多维数据在大数据、云计算和物联网等复杂环境中的持续增长,对其完整性验证提出了更高的安全性与高效性要求。以RSA与哈希算法联合构建的数据验证机制,在保障抗篡改性与签名不可伪造性的基础上,实现了对大规模、多维、动态数据的快速识别与精准校验。该方法不仅构建了可信数据交换的技术底座,也为数据流动与共享建立了更加稳固的信任机制。随着计算资源的进一步普及和轻量化算法部署的成熟,该类验证技术将在分布式数据安全治理体系中发挥更加核心的作用,为关键行业的数字基础设施安全提供可靠支撑。
参考文献
[1]张艳硕,隋吉达,严梓洋,等.基于ISRSAC-PSS算法的可证安全分组顺序聚合签名算法[J].信息网络安全,2025,25(2):215-227.
[2]谭涛,张黎明,闫浩文,等.基于RSA的矢量地图非对称无损加密算法[J].地理与地理信息科学,2024,40(6):45-50.
[3]杜建明,董国芳.基于自适应Merkle哈希树的动态数据流审计方案[J].计算机工程与设计,2024,45(8):2263-2271.
[4]张莉芸,谢晓宇.基于哈希算法的云存储数据完整性检验算法[J].计算机仿真,2024,41(8):423-427.
[5]洪文圳,李冬睿,沈阳.基于双哈希模糊布隆滤波器云存储数据融合[J].计算机工程与设计,2021,42(8):2152-2158.
文章出自SCI论文网转载请注明出处:https://www.lunwensci.com/jisuanjilunwen/82851.html