一种融合文件及内容分块的重复数据删除算法论文

SCI论文（www.lunwensci.com）:
 
   摘   要 ：重复数据删除对于文件增量同步、云存储和容灾备份等研究具有十分重要的作用和意义,能够大大地提高磁盘存 储的效率。结合现有的文件级和块级去重算法的优势,并针对基于内容的分块算法 CDC 容易因超大块而导致块大小方差变化 大的问题, 提出了一种融合文件及内容分块的重复数据删除算法 DMix。DMix 采用了面向文件级和块级的两阶段重复数据检 测及删除方法,并在快速双极值分块算法 RDE 的基础上,提出包含最大块阈值的内容分块算法 RDEL,使得 RDEL 在保持良 好的低熵字符串处理能力和抗字节偏移能力的同时,进一步降低了块大小方差。算法分析及实验结果表示, DMix 及 RDEL 能 够有效提升重复数据删除的效率,并能有效地降低 CDC 算法的块大小方差。

       关键词 ：内容分块 ；文件存储 ；重复数据删除


       【Abstract】：Data deduplication plays a very important role and significance in research such as file incremental synchronization, cloud storage, and disaster recovery backup, which can greatly improve the efficiency of disk storage. Combining the advantages of existing file level and block level deduplication algorithms, and addressing the problem of large block size variance caused by super large blocks in content based blocking algorithm CDC, a deduplication algorithm DMix that integrates file and content blocking is proposed. DMix adopts a two-stage duplicate data detection and deletion method for file level and block level, and proposes a content partitioning algorithm RDEL that includes the maximum block threshold based on the fast bipolar partitioning algorithm RDE. This allows RDEL to maintain good low-entropy string processing ability and anti-byte-offset ability, while further reducing block size variance. Algorithm analysis and experimental results indicate that DMix and RDEL can effectively improve the efficiency of deduplication and reduce the block size variance of the CDC algorithm.

       【Key words】：content chunking;file storage;data deduplication

       重复数据删除 [1-4] 是存储领域中用于消除冗余数据 和缓解数据爆炸式增长问题的一个热门研究课题,可以 有效地消除存储系统中的冗余数据和减少网络中传输的 数据量,大大地提升磁盘的存储效率,并节约存储成本 和网络带宽。NetApp 的研究 [5] 表明,重复数据删除可 以减少 95% 的备份系统存储空间, 72% 的 VMware 空 间, 30% 的 E-mail 和 35% 的文件服务。微软的报告 [1] 指出文件级的重复数据删除在 Windows 桌面机器的文 件系统中能节省 75% 的存储空间,数据块级的重复数 据删除能进一步节约 32% 的存储空间。在备份和归档系统中,数据冗余量甚至可能高达 80%-90%。重复数 据删除作为一种典型的消除冗余技术,主要通过删除存 储系统或传输数据流中重复的数据块或文件减少存储系 统中实际数据存储量。

       为了删除重复的数据,目前采用的数据去重策略主 要可分为 ：文件去重（File Deduplication, FD） 和分 块去重（Chunking Deduplication, CD）。其中, 文件 去重是将文件作为重复数据检测及数据去重的最小单位, 其优点是具备较大的检测和删除粒度,但缺点是无法解 决同一文件中的内部冗余数据问题,而且对于文件内容的局部变化非常敏感 ；而分块去重是以块为最小的单 位,将文件按照一定的策略分为不同的数据块,并进行 重复数据检测及删除。相对于文件级去重来说,分块去 重具有更好的灵活性和更高的去重效率,因此被广泛地 应用于各种海量数据存储系统中,如面向海量日志文件 及监控视频文件的云存储备份系统。

       目前,数据分块算法可分为基于固定长度分块算法 （Fixed-Size Chunking, FSC）和内容分块算法（Content- Defined Chunking, CDC） [6]。固定长度分块是按照 预先先义好的块大小对文件进行平均切分后,进行弱校 验值和 MD5 强校验值。由于分块长度固定,因此 FSC 的优点是简单、性能高,但对数据插入和删除非常敏 感,处理低效,无法根据内容变化进行调整和优化,即 面临因文件内容变化而导致的字节偏移问题 [7,8]。CDC 算法则采用可变的分块长度,将文件视为输入字符流,  通过一定的规则（特殊标志或算法）来寻找文件内容中 合适的切点进行分块切分。由于 CDC 算法能够较好地 解决 FSC 中的字节偏移问题,并提高冗余数据去重的 效率,因此成为目前重复数据检测及去重的主流方法。 但 CDC 算法面临的主要问题是如何合理地确定数据块 的切分,避免块大小的分差太大而影响吞吐率。

       为了提高 CDC 算法的效率,国内外不少人提出了许多 CDC 算法 [9]。例如,美国哈佛大学教授拉宾（Rabin）提 出了著名的 Rabin 分块算法 [9],其主要思想是将文件 视为字节流,通过计算滑动窗口中的 Rabin 指纹是否 等于预定值来确定切点的位置。Rabin 算法具有计算效 率高、结果对任意数据呈现出均匀分布的特点,常用于 进行快速比较并识别出重复数据。但 Rabin 指纹的计 算是一个较为耗时的过程,导致分块算法吞吐率较低而 影响系统的性能。Bjørner 等人 [10] 提出基于局部最大值 的 LMC（Local Maximum Chunking）算法,其主要 思想是在一个字节两边设置两个固定长度的窗口,通过 不断地移动字节和滑动窗口,当字节值为两个窗口的最 大值时,则以该字节作为切点进行切分。LMC 优点是 不需要计算哈希值,但需要额外的空间来存储固定窗口 内的字节值,且需要大量的比较。Zhang 等人 [11,12] 提 出基于非对称极大值的 AE（Asymmetric Extremum） 分块算法。AE 算法在字节后设置一个固定长度的滑动 窗口,字节前为可变长窗口,并通过字节值是否为固定 窗口的极大值来判断切点的位置。与 LMC 相比, AE 只 需要使用一个固定长度的窗口且将切点选择在固定长度 的末尾,因此减少了字节的比较次数。在 AE 的基础上,  Widodo 等提出一种快速非对称最大值 RAM 算法 [13]。

       与 AE 类似, RAM 同样使用了一个固定长度的窗口和 一个可变长度的窗口,将固定长度的窗口置于输入字节 流的开始,而可变长度窗口则置于固定窗口之后,极大 值则位于变长窗口之后,因此能够进一步减少了字节的 比较次数。在上述工作的基础,文献 [8] 和文献 [14] 中 也提出了一种快速双极值 RDE 分块算法,通过采用双 极值的判断策略来提升算法对低熵字符串的处理能力, 同时使用多字节的滑动窗口以控制窗口滑动速度和极值 计算粒度的方式,进一步缓解了分块算法吞吐量过低的 问题。RDE 本质上是在 RAM 的基础上进一步增加了极 小值。

       总的来说, 目前 Rabin、LMC、AE 和 RAM 等 CDC 算法已得到广泛的应用,并取得良好的效果。但仍面临 一些问题和不足,具体有如下几点 ：

       （1） FD 和 CDC 算法各有优缺点,大部分研究只考 虑单一算法, 难以满足实际应用场景的需要。CDC 容 易在文件重复率较高的数据中浪费大量的时间进行内容 分块。

       （2）RDE 算法能够有效解决 FSC 算法中的字节偏 移问题,但是无法避免因超大块而导致的块大小方差变 化大的问题。

       针对上述研究工作及存在的问题,本文的主要贡献 包括以下几点 ：

       （1）结合 FD 和 CDC 算法各自的优点,提出一种 融合文件及内容分块的重复数据删除算法 DMix,较好 地解决了实际应用场景中同时存在文件级及块级的不同 粒度重复数据问题。

       （2）针对 RAM 和 RDE 等算法中可能因超大块而 导致方差变化大的问题,结合块阈值提出一种改进的 RDEL 算法,在保持低熵字符串处理能力和抗字节偏移 能力的同时,通过一定的额外存储空间和计算量有效地 解决块大小方差过大的问题。

       （3）最后,通过算法分析以及在数据集上的实验, 证明了 DMix 及 RDEL 的有效性。

       1 重复数据删除算法 DMix

       下面提出一种融合 FD 和 CDC 的重复数据删除算 法 DMix（Deduplication by Mixing FD and CDC）, 首 先介绍方法的总体结构和流程,接着再具体介绍 DMix 中 内容分块算法 RDEL。

       1.1 总体流程

       由于在实际应用场景中,大量的数据主要以文件的 形式存在,其中既包含文件级的重复数据,同时也包含 块级的重复数据,因此 DMix 采用两阶段的方式 ：

      （1）第一阶段 ：文件级重复数据判断。

       具体包括 ：

       1）生成文件指纹。利用指纹技术为目标文件生成 唯一的指纹,并判断指纹是否已存在文件指纹库中。

       2）重复文件判断。若已存在相应的文件指纹,则 不存储文件,只需要从文件指纹库中返回相应的存储位 置索引信息,而不存储目标文件 ；若未存在相应的文件 指纹,则进入第二阶段的块级重复数据判断。

       （2）第二阶段 ：块级重复数据判断。

       具体包括 ：

       1）文件分块。使用 CDC 分块算法将文件切分成数 据块。

       2）生成数据块指纹。用指纹技术为各数据块生成 唯一的指纹,并判断指纹是否已经存在块指纹库中。

       3）重复块数据判断。若已存在相应的块数据指纹, 则不存储块数据文件,只需要存储指向相应块数据位置 的指针 ；若未存在相应的块数据指纹,则存储该数据块 并同时更新块数据及文件指纹库。

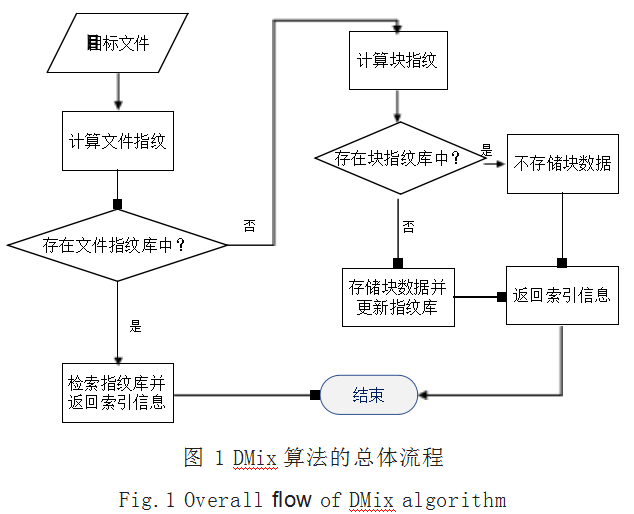
       DMix 算法的总体流程如图 1 所示。        常见的指纹生成算法包括 SM3、MD5 和 SHA-1 等。 在本文中主要采用了国产密码哈希算法 SM3。与单纯 的文件级或块数据级重复数据删除方法相比, DMix 算 法通过增加文件指纹库并存储每一个文件中各块数据信 息的方式,提供了一种粗粒度的重复数据检测判断方 法,从而避免一般 CDC 算法在文件级重复的情况下仍 然需要对文件进行分块和判断,大大地提升了重复数据 检测的效率。DMix 算法的伪代码如算法 1 所示。

       算法 1 DMix 算法

       输入 ：文件 file,固定窗口长度W,滑动窗口大小 N, 阈值 T

       输出 ：文件数据块索引信息 chunk_indexs function DMixChunking(file,W, T)

       fprint = HashDigest(file) // 生成文件指纹 if lookup(fprint, file_hash_table) then

       // 存在文件指纹则直接返回索引

       return file_hash_table[fprint]

       endif

       // 采用 CDC 算法分块,并返回各数据块索引 chunk_index =RDEChunking(file)

       // 更新指纹库中的索引信息

       update(file_hash_table, fprint, chunk_index) return chunk_index

       end function

       虽然 DMix 需要增加额外的文件指纹存储空间,但 由于文件和块数据的哈希指纹均为固定长度（如 SM3 为 256 位,而 MD5 为 128 位）,因此其存储空间只随 文件和块数据的数量增加而线性增长。

       1.2 DEL 算法

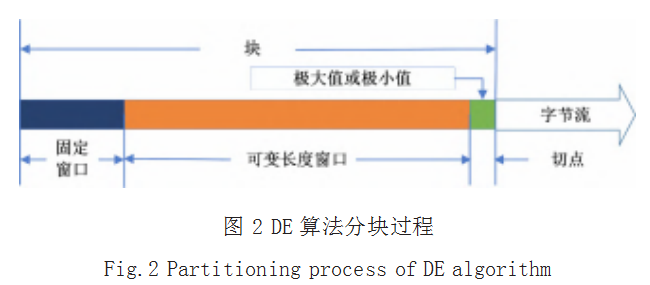
       文献 [8] 指出 RAM 算法中当固定窗口出现类似于 0xFF 这样的字节时,算法将难以发现极大值满足大于 等于 0xFF 的条件,从而导致块大小过大和块方差变大 的问题,并因此提出了 DE 分块算法,其分块过程如图 2 所示。        DE 由三部分组成 ：（1）长度为 W 的固定窗口 ； （2）可变长度窗口 ；（3）一个字节长度的滑动窗口。首  先, DE 将要分块的文件读取成字节流,并在字节流的  开始处设置一个固定长度为 W 的窗口。然后,按顺序  依次读入一个字节并进行比较,计算出固定窗口中的  极大值 Vmax  和极小值 Vmin。当滑动窗口中的值 X 满足  Vmax
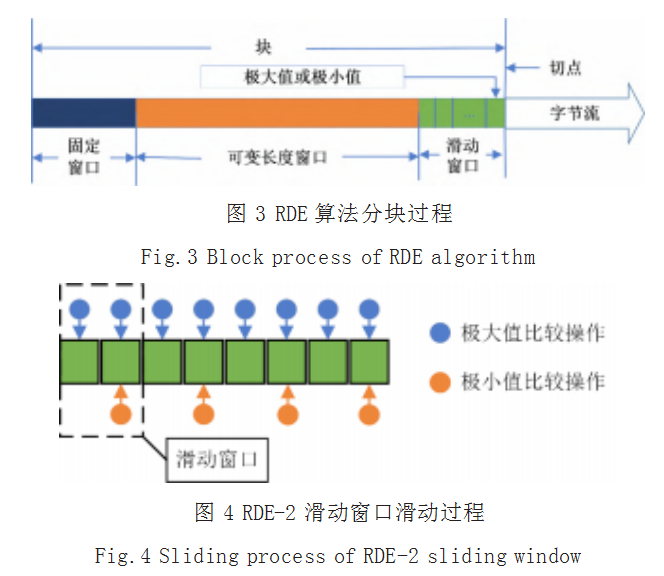
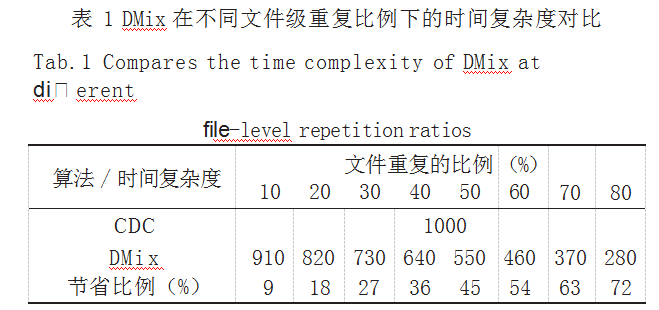
       在 DE 算法的基础上, 文献 [8] 还进一步提出了基 于多字节滑动窗口的 RDE 算法,即滑动窗口由 DE 中 的一个字节扩展为多个字节,其分块过程如图 3 和图 4 所示。

 

       显然, DE 和 RDE 本质上与 RAM 类似,只是通过 增加极小值的方式进一步提升了算法对低熵字符的处理 能力,进而缓解了块方差较大的问题。但 RDE 和 RAM 均无法完全避免超大块的出现,即当可变窗口中的字节 流出现大量重复内容且不满足切分条件时,将可能导致 超大块的出现,从而严重地影响了块方差的大小。

       以字节流 0x0B0AFF890E1278AEC2180E1278AEC2180 E1278AEC218 为例,假设固定窗口大小初始值为 4 个 字节,则 RAM 在固定窗口中的极大值为 0xFF,而 DE 的极大值和极小值分别为 0xFF 和 0x0A。显然, 如图 5 所示, 在整个后续滑动过程中, RAM 和 DE 都将无法 找到满足条件的切点,从而使得块大小过大甚至造成算 法失效无法分块。即 RAM 和 DE 及 RDE 均无法完全 避免超大块的出现和完全解决块大小方差过大的问题。

 

       针对上述问题, DMix 算法借鉴 RAML 的做法,在 DE 中引入块大小阈值,并提出相应的 DEL 算法。DEL 在 DE 的滑动窗口中同时保存一个全局的块大小阈值 T,并在滑动窗口过程中同时比较固定窗口和可变长度 窗口的总长度与 T 的大小。当总长度超过 T 时,即仍 未发现合适的切点,则以该位置作为切点位置。DEL 算 法的伪代码如算法 2 所示。

       算法 2 DEL 算法

       输入 ：文件 file,固定窗口长度 W,阈值 T

       输出 ：分块切点位置 I

       function DELChunking(file,W, T)

       i=1;// 初始比较位置

       chunk_index = [] // 切点位置列表 w_len=0

       while (X=readByte(file)) // 读取一个字节

       if w_len>=T then // 最大块阈值判断 w_len=0 // 重置窗口总长度

       chunk_index.append(i)

       continue

       end if

       if X>=Vmax then // 极大值判断

       if i>W then

       w_len=0

       chunk_index.append(i)

       continue

       // 极大值位置在固定窗口外,返回切点 end if

       Vmax=X // 更新极大值

       Vmax_pos =i // 更新极大值位置

       end if

       if X<= Vmin then // 极小值判断逻辑 if i>W then

       w_len=0 // 重置窗口总长度

       chunk_index.append(i)

       continue

       // 极小值位置在固定窗口外,返回切点 end if

       Vmin =X // 更新极小值

       Vmin_pos =i // 更新极小值位置

       end if

       i=i+1 // 更新比较位置

       w_len=w_len+1 // 更新窗口总长度 end while

       return chunk_index

       end function

       显然, DEL 具备与 DE 一样的低熵字符串处理能力, 且能有效地避免了超大块的出现,但代价是增加了计算 的次数,且需要事先指定块大小阈值。但我们认为这种 代价是必要的,因此超级块的出现不仅可能导致分块算 法失效,且严重影响了块方差的大小和存储效率。

       1.3 RDEL 算法

       类似地,参照上述 DEL 算法的思路,对 RDE 进行同样的扩展, 并提出相应的 RDEL（Rapid Double Extreme with Maximum Length） 分块算法。RDE 算法的伪代 码如算法 3 所示。

       算法 3 RDEL 算法

       输入 ：文件 file,固定窗口长度W,滑动窗口大小 N, 阈值 T

       输出 ：分块切点位置 I

       function RDELChunking(file,W,N,T)

       i=1 // 初始位置

       w_len=0 // 窗口初始长度

       chunk_index = []

       while (byte[N]=readNByte(file,N)) // 批量 读取 N 个字节

       if w_len+N>=T then // 最大块阈值判断 w_len=0 // 重置窗口总长度

       chunk_index.append(T-W+i)

       continue

       end if

       for j=0 to N-1 // 循环比较滑动窗口内极大值

       if byte[j]>=Vmax then

       if i>W then

       w_len=0 // 重置窗口总长度

       // 极大值位置在固定窗口外,返回切点 chunk_index.append(i)

       continue

       end if

       Vmax =byte[j] // 更新极大值

       Vmax_pos =i // 更新极大值位置

       i=i+1 // 更新比较位置

       w_len=w_len+1 // 更新窗口总长度 end for.

       // 滑动窗口最末尾字节与极小值比较

       if byte[N-1]<=Vmin then

       if i>W then

       w_len=0 // 重置窗口总长度

       // 极小值位置在固定窗口外,返回切点 chunk_index.append(i)

       continue

       end if

       Vmin = byte[N-1] // 更新极小值

       Vmin_pos =i // 更新极小值位置

       w_len=w_len+1 // 更新窗口总长度 end if

       end while

       return chunk_index

       end function

       显然, DEL 算法为 RDEL 算法中滑动窗口 N 为 1 的 特殊情况。

       2 DMix 算法分析

       2.1 总体分析

       与单纯基于 FD 或 CDC 的算法相比, DMix 需要 增加额外的文件存储空间用于存储文件指纹及文件对应 的块数据索引信息。假设采用 SM3 作为文件及数据块 的哈希指纹函数,则其每一个指纹均为 256 位,即 36 个字节。由于每一个目标文件均采用了 DEL 或 RDEL 算法进行分块,因此其块的数量是有限的,即存储空间 的大小只与文件的总数及每一个文件的块数量有关,且 为线性相关。这意味着 DMix 中所增加的额外存储空间 是可以忽略的。

       下面进一步对比分析 DMix 在同时出现文件级和 块级重复数据时的效率。简单假设共有 100 个目标文 件,且每一个文件级的重复数据比较及处理的平均时 间复杂度为 O(t),每一个文件中数据块的平均时间复 杂度为 O(r)。只考虑 CDC 算法时, 总时间复杂度约为 100×O(t)。不失一般性,假设 CDC 算法的平时时间复 杂度为 FSC 的 10 倍, 即 t=10×r 且 r=1。则当文件重 复的比例依次从 10% 到 80% 变化时,如表 1 所示给出 了 DMix 和 CDC 的时间复杂度对比及节省的时间比例。

 

       显然,从表 1 中的简单对比可以看出,随着文件级 重复数据的比例依次增加时, DMix 与单纯的 CDC 相比 所节省的时间开销也随之增加。特别是在海量数据存储 过程中,文件级的重复数据往往占据较大的比重,因此 DMix 可以明显地节省重复数据检测和删除的时间开销。

       2.2 字节偏移分析

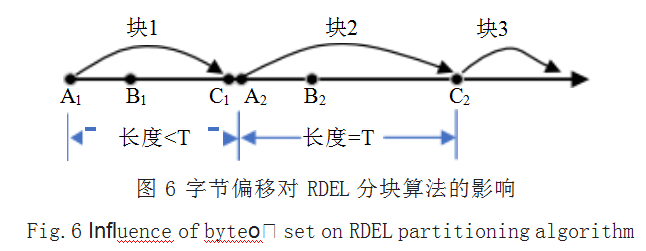
       分块时产生字节偏移问题是 CDC 算法中的一个核 心问题 [15], 即当前面的块插入、删除或者修改部分字 节时,后面块的边界也发生了变化。RDE 和 RDEL 均 将目标文件视作字节流,并主要根据字节的内容值来确 定切点的位置。与 RDE 相比, DMix 较 RDEL 虽然增加了块大小的阈值限制,但块内部字节的改变仅有很小的 概率会对之后的块造成影响。如图 6 所示说明了字节偏 移对 RDEL 算法的影响。

 

       图中 Ai 表示固定窗口的开始位置, Bi 表示固定窗 口的结束位置以及可变长度窗口的开始位置, Ci 表示块 的切点即块的结束位置,其中 i=1,2。区间 [Ai, Bi] 表示 固定窗口,区间 [Bi, Ci] 表示可变长度窗口。本文通过 块 1 和块 2 的字节发生变化的位置进行分析。

       （1）块 1（记为 [A1, C1]）

       由于块 1 的长度小于块长度阈值 T,因此在块 1 中 的删除不影响块长度边界的变化。对于修改或插入的字 节X, 设固定窗口 [A1, B1] 的极大值为 Vmax, 极小值为 Vmin,只要X 满足关于 Vmin

       （2）块 2（记为 [A2, C2]）

       与块 1 相同,块 2 中的删除不影响块长度边界的变 化,而修改操作只有当X ≥ Vmax  或X ≤ Vmin  时才有可 能影响 C2 的位置发生变化。而对于插入操作,由于块 2 的长度已经为最大块长度阈值 T,因此必然导致 C2 的 切点位置和块 3 的起点位置发生变化。考虑到在分块算 法中,超大块的出现概率本身非常小,因此只要阈值 T 的取值合理, RDEL 是能够最大程度上避免字节偏移问 题的影响,从而达到较高的重复数据删除率。

       2.3 块大小方差分析

       当分块算法划分的块大小越接近平均块大小时,块 大小的方差值越小,其存储效率越高。

       与文献 [8] 及 Bjørner 等的证明类似, 设 h 为区间的 长度,平均块大小为 2h+1,取一个大于 0 但不太大的乘 子M, RDEL 采用长度为 1 的滑动窗口,计算 RDEL 分 块算法在区间 [1, 2h×M] 上出现超大块（长度大于 T）的 概率。设 RDE 采用长度为 W 的固定窗口,则最小块的 大小为 W+1。由于块上每一个字节在概率上都是独立的, 块中的每一个字节都可能成为极大值也都可能成为极小 值。对于第 i个字节,若 W+i = T,则在区间 [1, W+i] 为 极大值和极小值的概率均为 1/(W+i), 没有极大和极小值的概率均为 1-1/(W+i)。取常数 c,在区间 [c×h+W+1, c×h+W+h] 均没有极大值和极小值的概率为 Π1 ≤ i ≤ h(1-1/ (W+i))=W/(W+h),那么在该区间内至少有一个极大值或 极小值的概率为 2h/(W+h)。将区间 [1, 2h×M] 分解为 h 大小的区间一共 M 个,则在第j 个区间 [(j-1)×h+1,j×h] 内没有极大值的概率为 1/j。最终在区间 [1, 2h×M] 上没 有极大值的概率为 Πi ≤j ≤ 2M(1/j)=1/2M!,同理,没有极小 值的概率也为 1/2M!。显然,当M 的值较大时,仅有极低 的概率会使得 RDEL 算法同时无法找到极大值和极小值。

       当 W+i=T 时, 第 i 个字节在区间 [1, T] 为极大值和 极小值的概率均为 1/T,则出现极大值或极小值的概率 为 2/T, 而没有出现极大值和极小值的概率为 1-2/T。显 然, 当 T足够大时,例如,在 Hadoop 2.0 中取其存储 块大小 128MB 作为阈值 T, 则同时不出现极大值和极 小值的概率接近无穷小。

       2.4 吞吐量

       下面从分块算法中滑动一个字节所需的最多操作数的 角度对各分块算法的吞吐量进行对比。参照文献 [8] 中的表 述,用 ADD 表示加法操作, MO 表示取模操作, HA 表示 哈希操作, C 表示比较操作, AS 表示赋值操作。RDE-N 和 RDEL-N 分别表示滑动窗口长度为N 的 RDE 和 RDEL 算法,(2+1/N)C 表示共有 (2+1/N) 次比较操作。如表 2 所示给出了各分块算法滑动一个字节所需要的最多运算 操作,其中 DEL 和 RDEL 暂时忽略索引数组的相关操作。

 

       从上面表 2 可以看出, DEL 和 RDEL 算法与其他 算法相比,其操作数均有所增加,意味着吞吐量下降, 主要原因是增加了 1 次块长度与阈值 T 的比较操作,以 及 1 次块长度的加法或重置操作以及 1 次长度的初始化 赋值操作。总体上来看, DEL 与 LMC 的吞吐量接近。

       3 实验与分析

       为了验证 DMix 及其 RDEL 算法的有效性,下面在 公开数据集的基础上与其他 CDC 分块算法进行对比。

       实验中使用 SM3 哈希算法进行块指纹的生成, 一个标 准布隆过滤器和两个哈希表进行文件指纹库和块指纹库 的构建以及重复数据的检测。

       实验采用 1 个公开的数据集和 1 个真实应用场景中 的数据集进行对比 ：

       （1）MOV 数据集。该数据集由人工拍摄的 9 个 4K 60FPS MOV 视频文件组成。数据集中也包含了部分视 频的剪辑版本,存在大量的重复数据,几乎不包含低熵 字符串,数据集总大小为 12.4GB。

       （2）日志文件数据集 LOG。该数据集为智慧化工 科研安全监管一体化平台中采集的一个时间段内的日志 文件,数据集总大小为 1023.7GB。

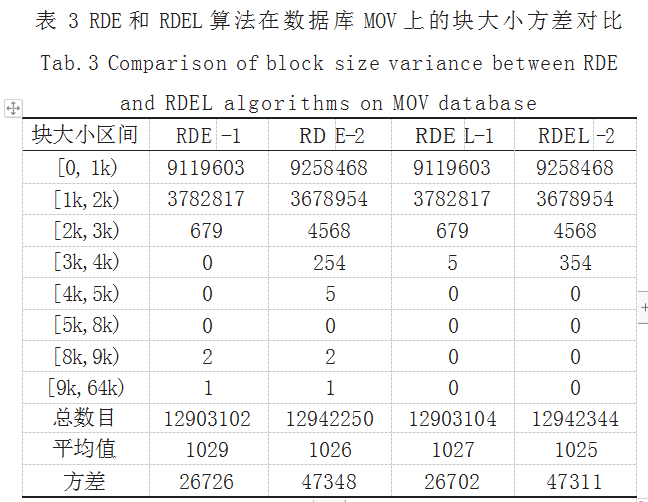
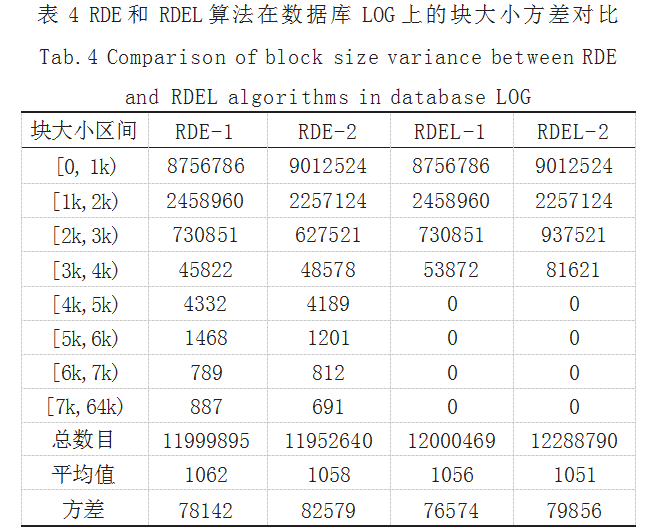
       因实验条件和篇幅限制,本实验只重点比较 RDE 和 RDEL 算法在这两个数据集上的块大小方差。考虑到 MOV 和 LOG 数据集中最大的块不超过 64000 个字节 （记为 64k）,因此为了便于对比,块大小阈值 T 取 3k。 实验结果如表 3 和表 4 所示。

 

       从表 3 和表 4 中的结果可以看出, RDEL-1 和 RDEL-2 在两个数据集上的块大小方差表现均优于相应的 RDE-1 和 RDE-2,都具有优秀的处理低熵字符串的能力,分块 稳定性受低熵字符串影响较小。由于受阈值 T 的影响, RDEL 中没有出现超大块（大于 3k 字节）,因此其块大 小方差也因此下降。显然,随着 T 值的下降,块大小方 差也相应下降,因此,合理的阈值 T 可以有效地优化块 大小方差。

       4 结语

       针对单一的文件级和块级去重算法所存在的不足, 以及内容分块算法容易因超大块而导致块大小方差变化 大的问题,本文提出了一种融合文件及内容分块的重复 数据删除算法 DMix,通过采用面向文件级和块级的两 阶段重复数据检测及删除方法,并在快速双极值分块算 法 RDE 的基础上,提出包含最大块阈值的内容分块算 法 RDEL,使得 RDEL 在保持良好的低熵字符串处理 能力和抗字节偏移能力的同时,进一步降低了块大小 方差。算法分析及实验结果也证明了 DMix 及 RDEL 能够有效提升重复数据删除的效率,并有效地降低了 CDC 算法的块大小方差。

       下一步将继续研究基于内容的分块算法中字节偏移 问题带来的各种影响,进一步研究如何更好地提高分块 算法的吞吐量,并扩展到分布式环境中。

       参考文献

       [1] MEYER D T,BOLOSKY W J.A Study of Practical Deduplication [J].ACM Transactions on Storage(ToS), 2012,7(4):1-20.
       [2] XIA W,JIANG H,FENG D,et al.A Comprehensive Study of the Past,Present,and Future of Data Deduplication[J]. Proceedings ofthe IEEE,2016,104(9):1681-1710.
       [3] 朱江,冀鸣,杨志成,等.基于重复数据删除技术的存储系统分 析[J].信息系统工程,2017(04):70-72+74.
       [4] KIM W B,LEE I Y.Survey on Data Deduplication in Cloud Storage Environments[J].Journal of Information Processing Systems,2021,17(3):658-673.
       [5] BADIA JM,NVE E,JIMENO J,et al.NetApp Deduplication for FAS and V-Series deployment and Implementation Guide[J].Technical Reporttr,2011,2009(1):141753-141753. 
       [6] PRATHIMA C,REDDY L S S.A Survey on Efficient Data Deduplication in Data Analytics[M].Soft Computing and Medical Bioinformatics.Springer,Singapore,2019:103-113. 
       [7] BJRNER N,BLASS A,GUREVICH Y.Gurevich.Content-Dependent Chunking for Differential Compression,the Local Maximum Approach[J].Journal of Computer and System Sciences,2010,76(3-4):154-203.
       [8] 巢赟.基于RDE分块算法的面向Spark平台重复数据删除技 术研究[D].广州:华南理工大学,2022.
       [9] RABIN M O.Fingerprinting by Random Polynomials [R].Technical Report,1981.
       [10] BJRNER N,BLASS A,GUREVICH Y.Gurevich.Content- dependent Chunking for Differential Compression,the Local Maximum Approach[J].Journal of Computer and System Sciences,2010,76(3-4):154-203.
       [11] ZHANG Y C,JIANG H,FENG D,et al.AE:An Asymmetric Extremum Content Defined Chunking Algorithm for Fast and Bandwidth-efficient Data Deduplication[C]// 2015 IEEE Conference on Computer Communications (INFOCOM).IEEE,2015:1337-1345.
       [12] ZHANG Y C,FENG D,JIANG H,et al.A Fast Asymmetric Extremum Content Defined Chunking Algorithm for Data Deduplication in Backup Storage Systems[J].IEEE Transactions on Computers,2016,66(2):199-211.
       [13] IDODO R NS,LIM H,ATIQUZZAMAN M.A New Content- Defined Chunking Algorithm for Data Deduplication in Cloud Storage[J].Future Generation Computer Systems, 2017(71):145-156.
       [14] YUN C,JINDIAN S.An Effective Way to Reduce Network Transmission in Backup System[C]//Proceedings-IEEE International Conference on Mobile Data Management, 2022:125-127.
       [15] ZHANG C J,QI D Y,LI W L,et al.Function of Content Defined Chunking Algorithms in Incremental Synchronization[J]. IEEE Access,2020(8):5316-5330.

关注SCI论文创作发表，寻求SCI论文修改润色、SCI论文代发表等服务支撑，请锁定SCI论文网！


文章出自SCI论文网转载请注明出处：https://www.lunwensci.com/jisuanjilunwen/76032.html