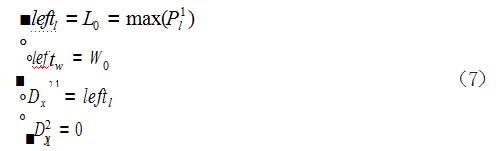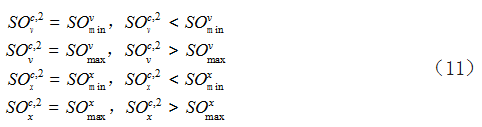SCI论文(www.lunwensci.com):
摘 要 :随着生活水平的提高,人们日常生活中使用的平面材料种类和大小越发丰富,在加工这些材料时,若采取订单顺 序的方式裁剪将产生大量的浪费。因此,个性化定制服务成为智能制造的主要竞争点,由此, 一种经过平面加工组装的矩形件 产品应运而生,此类产品要求多品种,订单批量小。为了满足合批要求的同时提高板材的利用率,本文分别使用贪心算法和粒 子群算法对平面排样进行优化和订单合批。
关键词 :矩形件 ;贪心算法 ;粒子群算法
Algorithm Optimization of Rectangular Layout and Combination
MAO Longwei, HOU Nanjian
(Chengdu Guoxin'an Information Industry Base Co., Ltd, Chengdu Sichuan 610041)
【Abstract】:With the improvement of living standards, the types and sizes of flat materials used in people's daily lives have become increasingly diverse. When processing these materials, cutting in order of orders will generate a lot of waste. Therefore, personalized customization services have become the main competitive point of intelligent manufacturing, giving rise to a type of rectangular product that has undergone flat processing and assembly. This type of product requires multiple varieties and small order batches. In order to meet the requirements of batch production and improve the utilization rate of sheet metal, this paper uses greedy algorithm and particle swarm optimization algorithm to optimize the planar layout and order batch production, respectively.
【Key words】:rectangular products;greedy algorithm;particle swarm optimization algorithm
0 引言
针对排样优化问题,在不考虑批次和材质的情况下 进行平面样板优化,需要满足一刀切原则 [1],在堆放的 过程中,严格按照从下到上,从左到右的顺序,合理选 择放入每个矩形件并完成堆积达到较高的板材利用率。 针对订单合批问题,需要考虑项目材质和所属批次,因 为同一订单下存在多个项目,批次设置的初心是提高时 间的响应性,因此同一订单必须放入同一批次中。在这 一约束下,从项目到堆的过程需要考虑批次和堆的一致 性,从堆放置到原片的过程中,需要保证同一原片下的 堆批次和材质保持一致,求得较优的平面排样方案使得 板材的利用率最高 [2]。
1 排样优化问题算法建模与求解
1.1 贪心算法建模与求解
以宽度为分类依据,经 Lingo 编程计算数据集中不 同宽度数量,将相同宽度的项目拼接并计算拼接后总长 度,根据总长度对宽度尺寸分类, 一类是总长度超过原 片长度的,另一类是不超过原片长度的。对于总长度超 过原片长度的宽度尺寸,我们将这一类的项目优先进行 二阶排样 ;对于总长度不超过原片长度的宽度尺寸,我 们将这一类项目优先进行三阶排样 [3]。
编写 Lingo 程序对不同宽度 wn 求解排样最优组合, 即宽度最优解 wα ,最优宽度下长度最优解 lα ,最优宽度 下长度其次最优解 lαn 进行迭代,采用相同的方法,依次对不同宽度 ln 进行长度优化,至此得出第一块模板的 最优解,然后将剩余矩形件按照以上思想继续进行优化 排列,最终可得到矩形件最优化排版。但该方法的自动 化程度较低,优化步骤较为复杂,实现效率较低。
1.2 粒子群算法建模与求解
模型假设与符号说明如表 1 所示, 其中涉及长度和 宽度单位为 mm、面积单位为 m2、比率单位为 %。
为每个项目设定三个决策变量,分别决定该项目是 否旋转,该项目与哪个项目成堆,该项目的堆放优先级。 首先是旋转,对于每个项目的x1i 而言,若x1i>0.5, 则进行 旋转,否则不旋转,旋转后项目的长与宽如式(1)所示 :
对于某个项目而言,与其成堆的项目序号 indexp 如 式(2)所示进行计算,式(2)中, x2i 为 0~1 之间的数。
堆的堆放过程采取从 ID 为 1 的序号开始,逐步进 行判定,若 indexp 的长或宽与该项目一致,且尚未成堆, 则该项目与 indexp 项目成堆, 若它们的长度一致则在宽 度上堆加,否则在长度上堆加。使用如式(3)、式 (4) 所示的公式 :
若 indexp 已经成堆,则该项目对 indexp 所属的堆的Ml 与Mw 进行比较。除了考虑长宽一致的条件外,还需满足 该堆或项目已有的长度或宽度在增加该项目后不超出原片 的大小。在堆放入原片的过程中,若该原片无堆, 则该堆 可直接放入,并使用如式(5)所示的公式设置堆的坐标 :
此时堆的堆放 X 轴为 0,因此可堆放的剩余长度与 原片长度一致 leftl=L0,可堆放的剩余宽度为 leftw=W0-Dw。 按照优先级的顺序寻找满足 {Pl ≤ leftl,Pw ≤ leftw} 的堆, 若 存在该堆,则由如式(6)所示的公式设置该堆的坐标 :
更新可堆放的剩余宽度 leftw=leftw-Pw1,2,再次按照 优先级的顺序寻找满足 {Pl ≤ leftl,Pw ≤ leftw} 的堆,若 不存在这样的堆,则向右开始堆积,由如式(7)所示 的公式设置剩余原片的长度与下一堆的起点 :
重复上述步骤,直到所有堆放入原片,板材利用率总目标函数 [4] 如式(8)所示 :
粒子群算法使用协同进化策略更新每一代粒子的位置,具体过程如式(9)、式(10)所示 :
式中,{c1, c2, c3} 分别为权重、个体学习因子和群 体学习因子, 取 0.7、0.5、0.5, 使用如式(11) 所示的公式进行边界调整。
同时减少早熟的概率 [5],使用如式(12)所示的公式进行变异操作 :
重复使用式(9)、式(10)、式(11) 与式(12), 直到迭代次数达到设定的上限,输出最优解。粒子群算 法收敛曲线如图 1 所示,板材的利用率稳定在 0.8439、 0.8370、0.8544、0.8438。
板材利用率直方图如图 2 所示,使用粒子群算法对板 材进行优化后,每块板材的利用都达到了较高的使用需求。
2 订单合批问题算法建模与求解
订单合批与排样优化相比,仅在堆的判定和原片的 判定上存在差异,为每一个订单设置堆的所属批次,当 项目开始成堆时,除了判断该项目与对应项目或堆的长 或宽相同,叠加后不超出原片大小约束外再添加材质与 批次相同的约束,原片在放入第一个堆时,该原片便 具备了材质和批次的属性,仅可放入材质和批次相同的堆。使用如式(13)所示的罚函数对批次的面积和数量进行约束,第二、三项为惩罚项。
板材的利用率稳定在 0.6141、0.585、0.5855、0.5895、 0.5854。加了合批次后,当某批次内的项目消耗殆尽 时,容易出现较大板材浪费,这属于合批次生产中无法避免的现象,除此情况外的板材中,板材的利用率较为 可观,绘制部分板材缩略图如图 3 所示。
3 模型评价
对于数据较大的模型,贪心算法模型的计算效率不 足,难以实现最优模型的优化,通过粒子群算法改进板 材堆积的计算过程,对该平面模型进行排样优化,大幅 度提高了板材的利用率,灵活解决了订单合批问题,满 足了实际生产加工需求。
参考文献
[1] 宋连超,朱建良,张彤.矩形件排样优化贪婪算法及系统开发 [J].哈尔滨理工大学学报,2007(01):29-31+35.
[2] 邓文浩.满足“一刀切”约束的矩形件排样问题研究[D].大 连:大连海事大学,2019.
[3] 张子成.基于矩形拼接的“一刀切”矩形排样优化设计[J]. 现代制造工程,2018(04):103-107+157.
[4] 陈钊.离散粒子群算法在矩形排样问题上的应用研究[J].安 徽职业技术学院学报,2018,17(02):19-21+28.
[5] 张浩.面向板式产品定制生产的组批与排样协同优化方法 [D].广州:广东工业大学,2019.
关注SCI论文创作发表,寻求SCI论文修改润色、SCI论文代发表等服务支撑,请锁定SCI论文网!
文章出自SCI论文网转载请注明出处:https://www.lunwensci.com/jisuanjilunwen/74912.html