大规模 MIMO 系统能量效率优化问题论文

SCI论文（www.lunwensci.com）
 

　　摘要：本文分析讨论了导频发射功率对能量效率的影响,以天线数目、导频功率和数据功率作为待优化变量的能效函数,采用交替优化来得到最大值。针对天线数目优化,运用LambertW函数推导出最优天线数目的闭式表达式,然后采用黄金分割法交替迭代目标函数。

　　关键词：能量效率；大规模MIMO；功率分配；LambertW函数

　　Optimization Problem of Energy Efficiency for Massive MIMO Systems

　　【Abstract】：The influence of pilot transmission power on energy efficiency is analyzed and discussed.The number of antennas,pilot power and data power are taken as the energy rate function of the variables to be optimized,and the maximum value is obtained by alternating optimization.In order to optimize the number of antennas,the closed-form expression of the optimal number of antennas is derived by using the LambertW function.Then the golden section method is used to alternately iterate the objective function.

　　【Key words】：energy efficiency;massive MIMO;power distribution;LambertW function

　　0引言

　　近年来随着无线通信的发展,业务需求量不断增加,随之而来的能耗问题也逐渐成为专家和学者研究的对象[1]。

　　文献[2]从能量效率的角度比较了大规模MIMO下行链路模型下最大比传输预编码与迫零预编码的系统性能。文献[3]通过用户选择的方式降低了能量损耗,提高了系统效率。文献[4]通过多点传输与波束成型等方式实现了频谱效率的优化,间接提升了能量效率。

　　本文在信道状态未知的单小区多用户上行链路大规模MIMO系统下对大规模MIMO系统上行链路的有效速率[5]和能耗模型[6]分别建模,考虑一种新的与天线数目、导频发射功率和数据发射功率有关的能量效率函数,并且引入LambertW函数推导出了使能量效率最大化的最优天线数目的闭式表达式,最后采用迭代的方式达到最大化能量效率的目标。

　　1系统模型

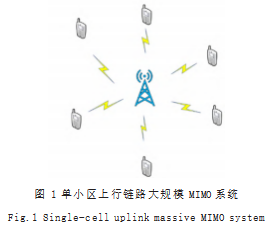
　　本文的系统模型考虑一个单小区多用户上行链路大规模MIMO系统。小区的中央配备一个具有M根发射天线的基站,在小区的内部,基站的四周随机分布了K个用户,这些用户都只有一根接收天线,并且满足M>>K,如图1所示。

　　定义T为一个相干间隔长度,τ是每个相干间隔中的导频长度数。所有用户同时发送长度为τ的相互正交的导频序列。假设K个用户所组成的导频矩阵为Ψ,当K个用户同时发射导频信号时,基站处接收的信号可以写成如式（1）所示的形式：

　　pu表示每个用户在用户端发送的数据功率,n为信道噪声矩阵,H是基站与用户之间的瑞利衰落信道矩阵,H的列表示为hk,hk满足均值为0,方差为1的复高斯分布,方差表示大规模衰落系数。根据文献[5],在基站处采用最小均方误差信道估计。

　　2能效问题的描述

　　2.1可实现的上行链路有效速率

　　为了消除接收信号之间的干扰,本文采用最大比合并信道检测技术[5]来获得上行链路传输的信号。

　　考虑到信道估计导频,采用类似文献[7]中的Jenson不等式的方法,在文献[5]中给出了运用MRC检测技术得到的可实现有效速率的下限如式（2）所示,其中(1−r/T)为传输中有效载荷在整个时隙中的占比。

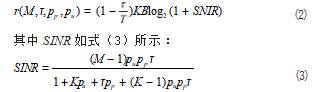
　　SINR表示分离的信噪比,B表示系统带宽,T表示一个相干间隔长度,M为基站处的天线数目。

　　2.2能耗模型

　　能耗模型的建立是通过测量无线通信网络各个节点的能耗并进行线性叠加[6],这种情况下的能耗模型可以写为如式（4）所示的形式：

　　2.3目标能效函数描述

　　根据上文推导出的模型,结合文献[7]中的定义,即大规模MIMO系统的能量效率可以表示为有效和速率与系统能耗的比值,可以推导出能量效率的优化表达式如式（5）所示：

　　反证法的思想证明了当时能量效率达到最大。

　　3天线数优化

　　由优化问题式（6）的目标函数可知,大规模MIMO系统的能量效率函数是一个多变量优化问题。本文引入LambertW函数并求解出能量效率最大化条件下的最优天线数目的解。

　　其中M为变量,p1,p2,p3,p4,a为常数,并且均为正数。由于天线数为整数,所以最终的最优天线数可以表示为如式（7）所示：

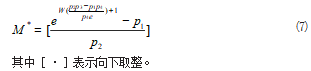
　　4数据功率与导频功率优化算法

　　由于本文的能效函数关于天线数、导频发射功率和数据发射功率均为凸函数,考虑采用交替优化算法对目标函数的子问题进行迭代优化。

　　具体算法过程如下：

　　5仿真结果

　　如图2和图3所示,揭示了本文所采用的能效函数以及文献[7]和文献[8]所提出的能效函数用户数量和最大能量效率、最优天线数之间的关系。从图2中可以明显看出本文提出的算法与文献[7]和文献[8]提出的能效函数算法相比可以获得更大的能量效率。

　　如图4所示为数据功率与导频功率之比和相干间隔长度之间的变化关系图,从图4中可以发现数据功率与导频功率之比先快速减小,再逐渐减小速度变慢,相干间隔短的情况对应于高速移动的场景。

　　6总结与展望

　　本文研究了大规模MIMO系统上行链路在信道未知的情况下的能量效率优化问题,仿真结果表明,与现有的算法相比,本文采用的算法能够获得更高的能量效率,并且需要的天线数也比现有模型少,在提高系统性能的同时降低了成本。

　　参考文献

　　[1]JIANG B,QU L,HUANG Y,et al.Energy Efficiency Optimization in Massive MIMO Secure Multicast Transmission[J].Entropy,2020,22(10):1145.

　　[2]NANGIR M,GHARAGEZLOU A S,IMANI N.Comparison of the MRT and ZF Precoding in Massive MIMO Systems from Energy Efficiency Viewpoint[C]//2022 30th International Conference on Electrical Engineering(ICEE).IEEE,2022:803-807.

　　[3]周好生,韩韧,占庆杰.多用户MIMO系统上行链路的用户分组选择[J].软件,2019,40(06):81-87.

　　[4]任天昊.FD Massive MIMO协作多点传输场景下提升系统频谱效率的算法研究[J].软件,2019,40(9):115-119.

　　[5]CHENG H V,BJÖRNSON E,LARSSON E G.Uplink Pilot and Data Power Control for Single Cell Massive MIMO Systems with MRC[C]//2015 International Symposium on Wireless Communication Systems(ISWCS).IEEE,2015:396-400.

　　[6]NANGIR M,GHARAGEZLOU A S,IMANI N.Comparison of the MRT and ZF precoding in Massive MIMO Systems from Energy Efficiency Viewpoint[C]//2022 30th International Conference on Electrical Engineering(ICEE).IEEE,2022:803-807.

　　[7]NGO H Q,LARSSON E G,MARZETTA T L.Energy and Spectral Efficiency of Very Large Multiuser MIMO Systems[J].IEEE Transactions on Communications,2013,61(4):1436-1449.

　　[8]TIAN G,GUOMIN L.Energy-Efficient Power Control Optimization Algorithm in Massive MIMO Systems[C]//2020 IEEE 6th International Conference on Computer and Communications(ICCC).IEEE,2020:251-255.

关注SCI论文创作发表，寻求SCI论文修改润色、SCI论文代发表等服务支撑，请锁定SCI论文网！

文章出自SCI论文网转载请注明出处：https://www.lunwensci.com/jisuanjilunwen/74801.html