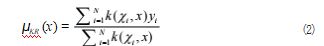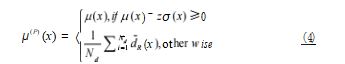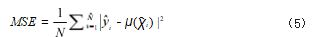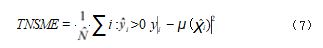SCI论文(www.lunwensci.com)
摘 要 :估计能源动力机器人在不可预测环境中的碰撞安全距离对保障其安全性极为关键。然而,机器人运动距离的估计 通常是个时间成本高的过程,且要求传感器必须具备高精度。为此,我们采用了一种结合高斯过程回归与正向运动学核方法的 策略,此方法能够更有效且准确地估量碰撞距离。通过实验验证,此策略即便在噪声较多的复杂环境中训练,其性能相较于传 统标准几何方法在距离估计方面的效率提高了近 70 倍,准确度也提升了 13 倍,证明了其显著的优势。
Modeling, Simulation and Experimental Research on Energy Powered Robot System
ZHAO Tian1. QIAN Jing1.2. ZENGYun1.2
(1.School of Metallurgy and Energy Engineering, Kunming University of Science and Technology, Kunming Yunnan 650093;2.Yunnan University Hydraulic Machinery Intelligent Testing Engineering Research Center, Kunming Yunnan 650093)
【Abstract】:Calculating the collision distance of energy powered robots is crucial for evaluating their safety in unpredictable environments. The estimation of robot motion distance is a time-consuming operation, and the accuracy requirements of the sensors used to measure the distance are strict. Therefore, a Gaussian process regression and forward kinematics kernel method is proposed to effectively and accurately estimate collision distance. Experimental verification shows that even if Gaussian process regression is trained in a noisy and complex environment, the proposed method can still shorten the distance by 70 times and improve accuracy by 13 times compared to traditional standard geometric methods.
【Key words】:gaussian process;distance calculation;kinematics
0 引言
为了确定机器人操作臂在碰撞或安全状态下是否处于 可行位置,需要分析碰撞检测器所产生的二进制信号 [1]。 并且为保证机器人在不可预测环境中的安全运动,机器 人的安全操作依赖于精确设定碰撞警戒距离 [2]。此外, 为了确保机器人之间能有效避免相互碰撞,模拟环境中 需要准确反映若干参数,如物体间的距离 [3]、接触的分 辨率 [4] 以及触觉反馈力度 [5]。这些因素共同作用于机器 人运动的控制与安全性。
能源动力机器人碰撞规划方法可分为以下两大类方法 :
(1)几何方法 :计算碰撞距离的典型方法是利用几 何模型。刘劲松等研究人员提出了一种表示机器人手臂各个部分的方法,将其抽象为圆柱体和关节节点。这种 方法首先通过深度相机收集点云数据,并将其分解为多 个较小的点云群组, 继而应用 GJK(Gilbert-Johnson- Keerthi)算法进行碰撞距离的精确计算 [6]。
(2)基于感知的距离字段方法 :段帅帅等人创建基 于深度传感器的机器人碰撞距离估计方法 [7]。在工作空 间、距离方程使用深度图定义,其中包含每个像素的深 度值,以此来计算碰撞。
我们提出一种使用高斯过程回归和正向运动学核方 法来有效地准确估计碰撞距离。所提出方法相比几何方 法及基于感知的距离字段方法都具有优势,利用其中的 轨迹优化技术,可实现时间优化。
1 方法
1.1 回归模型
在数据的多维输入下,回归模型可以产生多维向量 进行输出 [8]。在复杂背景下评估时,设定被测量传感器的 碰撞距离是真实距离和偏差距离的总和,如式 (1) 所示 :
核回归模型的高斯过程允许环境复杂性随着时间的 推移不断变化,回归模型如表 1 所示。
使用概率分布,选取预测输出的所有训练数据点的 加权和查询点的值。单次预报方程查询点如式 (2) 所示 :
其中, k 是内核函数。KR 不需要训练任何权重来估计 预期值。通过均值和协方差定义内核函数。使用平均值和 内核函数 k,计算空间所有可能的先验分布如式 (3) 所示 :
η2 是测量值中的测量噪声方差。该噪声项可以看作 是一个可以训练数超参数的数据集。
1.2 快速路径并行化策略
在本节中,我们定义了一个模型f: RD 喻 R,精确 估计机器人配置。通过 dR(x)估算潜在不确定性。定 义了一个混合距离,使用 GP 平均值作为预测值估计无 碰撞区域的距离如式 (4) 所示 :
其中 P 表示相关置信水平, z 代表标准偏差数, Nd 代表要采集的样本数, dR (.)可以降低传感器噪声的影响 来增强模型健壮性。
2 实验结果分析
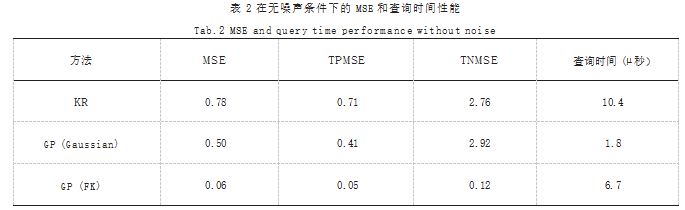
2.1 准确性和查询时间
在本节中,我们将评估 GP 模型的性能并通过精度 和计算时间进行分析。均方误差错误(MSE)和模型查 询时间来评估模型鲁棒性。MSE 定义如式 (5) 所示 :
若测试集 χ(ˆ)有 N( ˆ)个元素,则是真值集 χ(ˆ)标签,以及 µ( · ) 提供预测距离。对模型进行噪声距离评估训 练,使用无噪声距离评估来获得计算 MSE。若为 正(无碰撞)或负(碰撞中),我们称之为真正 MSE (TPMSE) 和真正 MSE 负 MSE(TNMSE)。TPMSE 和TNMSE 定义如式 (6)、(7) 所示 :
如表 2 所示显示了模型的性能以及每个方法的 MSE 和查询时间,其平均相撞距离为 1.7.GP 方法与 FK 内 核一起使用时的 MSE 显著降低,且由于 FK 内核与工作 区中位置的先验性关系,内核在建模精度上有了很大的 提高。
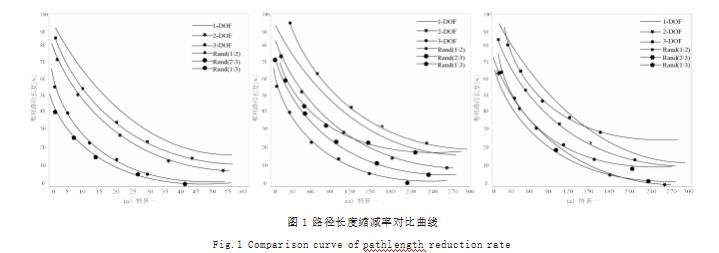
2.2 收敛速度的比较
首先,由于有必要预先确定机器人数量, 运行模拟 时仅提出方法使用, 用于缩短路径的接头,并对其进行 性能比较来确定算法的最佳情况。如图 1 所示显示了每 个迭代步骤路径长度缩减率对比。
3 结语
在本文中,提出了一种高斯过程回归和正向运动学 核方法来有效准确地估计能源动力机器人碰撞距离。提 出方法利用 GP 回归和 FK,进行轨迹预测,并且使用 FK 核查询 GP 模型距离估计比几何方法快 70 倍。模型 的精确度大大超过了其他回归技术。还引入了一个基于 置信度混合模型使用 GP 平均值作为以下区域的预测距离,提出方法在狭窄通道环境中的性能优越。
参考文献
[1] 司国斌,王春霞.农业采摘机械手路径规划—基于云平台 和Q学习算法[J].农机化研究,2021.43(10):23-27.
[2] 刘侃,陈琳,喻欣.基于遗传算法的机械手路径规划优化[J].内 蒙古科技与经济,2020(22):114-115.
[3] 李振浩,管声启,肖旭,等.一种新型的仿生机械手结构设计与 运动学仿真[J].西安工程大学学报,2020.34(5):56-62.
[4] 李伟峰,张久昌,宁林祥,等.基于数据手套的仿生机械手控制 与示教再现[J].铸造技术,2020.41(9):861-866.
[5] 汪琳.基于SCARA机械手的采茶机器人研究[D].合肥:中国 科学技术大学,2021.
[6] 刘劲松.基于时间最优的六轴关节机械手轨迹规划研究[D]. 武汉:湖北工业大学,2020.
[7] 段帅帅.基于多爪机械手的不规则物体抓取技术[D].太原:中 北大学,2020.
[8] 吴国洋.基于GRN模型精密机械手末端映射关系[J].重庆理 工大学学报(自然科学),2020.34(6):154-159.
关注SCI论文创作发表,寻求SCI论文修改润色、SCI论文代发表等服务支撑,请锁定SCI论文网!
文章出自SCI论文网转载请注明出处:https://www.lunwensci.com/jisuanjilunwen/74213.html