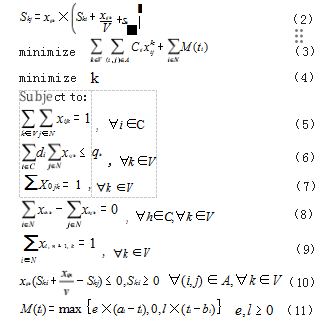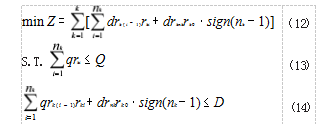SCI论文(www.lunwensci.com)
摘 要 :近年来, 随着现代物流业的发展, 车辆、传统批发模式和仓储空间发生了变化。特别是采用不同的配送方式, 有效控 制运输时间和成本,成为城市车辆布局的重要目标。因此,为确保最大限度地降低成本,使车辆行程路径最合理, 本文以最小化成 本为目标,研究带时间窗的车辆路径问题,分别采用软硬时间窗建立数学模型,为了加快遗传算法的收敛速度和寻优能力, 采用局部 搜索算法和遗传算法相融合的混合遗传算法,同时通过实例论证了改进遗传算法在求解带时间窗的车辆路径优化问题方面的有效性。
关键词 :遗传算法,带时间窗,车辆路径优化
Research on Vehicle Path Optimization Method with Time Window Based onImproved GeneticAlgorithm
SONG Yu
(Guangzhou University of Business and Technology, Guangzhou Guangdong 510850)
【Abstract】:In recent years, with the development of modern logistics industry, vehicles, traditional wholesale models, and storage spaces have undergone changes. Especially adopting different delivery methods to effectively control transportation time and costs has become an important goal of urban vehicle layout. Therefore, in order to ensure maximum cost reduction, making the vehicle travel path the most reasonable, this article aims to minimize cost and study the vehicle routing problem with time windows, using both soft and hard time windows to establish mathematical models, in order to accelerate the rate of convergence and optimization ability of the genetic algorithm, a hybrid genetic algorithm combining local search algorithm and genetic algorithm is used. At the same time, an example is given to demonstrate the effectiveness of the improved genetic algorithm in solving the vehicle routing optimization problem with time windows.
【Key words】:genetic algorithm;with time window;vehicle path optimization
遗传算法是用于研究人工系统的自然遗传现象和适 应性行为的全局并行搜索算法,基于生物进化和“优胜 劣汰”的遗传思维。遗传算法为解决不依赖于特定领域 的复杂系统优化问题提供了一个通用框架。改进遗传算 法,采用交叉算子,结合点交叉算子和段交叉算子,参 照精英保留策略提出允许延时的链接概念,然后利用局 部搜索策略进一步提高求解质量。与简单的遗传算法相 比,改进的遗传算法具有更好的全局优势搜索能力和更 快的收敛率 [1]。
1 问题描述及数学模型
1.1 带软时间窗车辆路径问题
带软时间窗车辆路径问题可以表示为 :假设中心仓库有车辆载重为 q,车辆数量用集合表示为 V={x}, x= 1.2.…,k,负责配送 n 名客户的货物,客户数量用集合表 示为C={i}, i=0.1. …, n,(i=0 时代表中心仓库)。客户的 货物需求量计作g(g < q), i 的时间窗表示为 [ai,bi](ai 表 示最早时间 , 更早则需要等 ;bi 表示最迟时间,晚了则有违 约费用)。客户 i 与客户j 的距离用xij 表示。 Ski(Ski ∈ [ai, bi])表示 k 车辆到达客户 i 的时间。车辆在客户 i 处的 服务时间表示为 sti。在这种情况下要保证用尽可能少的 车辆走尽量短的路,应该如何规划行车路线 [2]。下面给 出多目标优化模型,函数公式如式(1) - 式(11)所示 :
说明 :函数(3)、函数(4)保证在成本最少的基 础上所用车辆尽量少 ;函数(5)保证每名客户有且仅 有一辆车辆服务 ;函数(6)保证每辆车的货物不超过 车辆容量和重量限制 ;函数(7)、函数(8)、函数(9) 保证车辆运输系统处于闭环状态,每辆车只离开仓库一 次且服务完客户后才会返回 ;函数(10)保证当车辆不早 于到达下一客户 ;函数(11)保证车辆尽量满足所有客 户的时间窗要求。
1.2 带硬时间窗车辆路径问题
带硬时间窗车辆路径问题可以表述为 :当库中可用 车辆为 k,每辆车载重为 Q 时,假设每辆车的最远行程 都是 D,且需要向 n 和地点配送货物,配送点货物需求 量为 qi (i=1.2.…,n),要求货物在时间窗 [Ei,Li]( 分别表示 配送点可接受的最早以及最迟送达时间)内送达,如何 在满足约束条件的情况下使总里程数最短。可将各点位 之间的距离表示为 dij (i,j=1.2.…,n), 仓库到客户的距离 用 d0ij 表示, nk 代表 k 车辆运送 rki 的顾客数,集合 Rk 表 示 k 车辆的路径, rk0=0 表示中心仓库,其中的元素表示 点位 i 在路径 k 中的顺序为 i 且不包含中心仓库。drk(i-1)rki 用来表示 k 路径中客户 i=1 与客户 i之间的距离, drknkrk0 表示 k 路径中第 nk 名顾客与中心仓库的距离, k 路径中 i 顾客的需求量表示为 qrki, Sk(i-1) 则是 k 路径中点位 i-1 所 等待的时间 [3]。数学模型如式(12) - 式(21)所示。
说明 :函数(1)作为目标函数要求总里程最短 ;函 数(2)保证每条路径上各客户的货物需求量之和不超过 配送车辆的载重量 ;函数(3)保证每条配送路径的长度 不超过配送车辆一次配送的最大行驶距离 ;函数(4)保 证每条路径上的客户数不超过总客户数 ;函数(5)保证 每个客户都得到配送服务 ;函数(6)代表每条路径的客 户的组成 ;函数(7)限制每个客户仅能由一台配送车辆 送货 ;函数(8)表示当第 k 辆车服务的客户数≥ 1 时, 说明该台车参加了配送, 则取 sigm(nk)=1. 当第 k 辆 车服务的客户数 <1 时,表示未使用该台车辆,因此取 sign(nk)=0 ;函数(9)、函数(10)为时间窗约束。
2 带软时间窗车辆路径问题改进遗传算法
启发式算法是目前解决复杂优化问题的有效方法, 不需要或只需要较少先验问题信息。该算法具有通用 性,可以适应不同领域的优化问题,并经常获得较为满 意的解决方案。
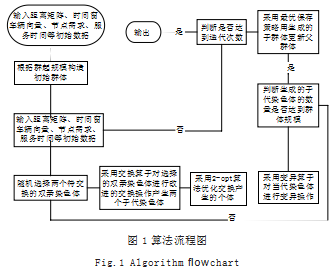
2.1 算法流程
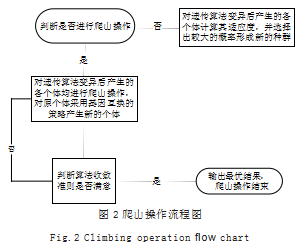
启发式算法流程图如图 1 所示, 在算法结束最后一 个群体的最优个体即为可行解。
2.2 算法分析
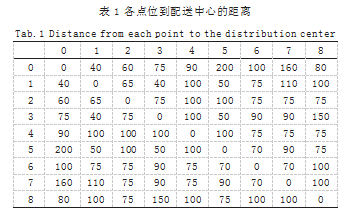
求解验证以某物供中心的 1 个中心仓库以及 8 个点位需求为例, 各点位需求量为 qi(单位 :t)。这些点位 由容量为 8t 的车辆进行服务,各点位到配送中心的距 离如表 1 所示。
客户服务时间 si (单位 :h)以及点位要求时间窗 如表 2 所示。同时给出任务特征及要求,要求合理安排 车辆路线缩短总路程,减少使用车辆。
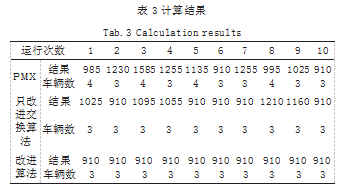
固定车辆能力时,算法参数为 :组数 40.代数 200.组收敛阈值平均值设置为 0.85.组偏差阈值设置 为 0.05.交换概率设置为 0.8.突变概率设置为 0.02. 早到惩罚设置为 10.迟到惩罚设置为 50.车辆的固 定成本设定为 500(时间惩罚和车辆固定成本的确定 应根据行驶路程数量级确定)。如表 3 所示显示了几种 不同遗传算法结果的比较。如果交换算子使用部分映 射(PMX),则表示只有改进的交换算法仅对文本使用 改进的交换算法,改进的算法是添加改进的交换算子 2-opt 算子后的算法。
2.3 结论
(1) 在使用改进的交换算子获得的优化结果中, 50% 得到了最优解,远好于只有 20% 的交换算子使用 PMX 获得的最优解。
(2) 增加了改进的 2-opt 运算遗传算法,通过交换 操作后个体的局部搜索,搜索到更完善的能力,在实验 过程中得到 100% 的最优解 [4]。通过进一步观察, 加入 局部寻优操作的改进遗传算法一般在 20 次迭代后得到 最优解。可以看出,改进后的算法在解的质量沉降时间 方面有所改进。
(3) 由于文本适配功能增加了对车辆固定成本的处 罚,因此该实验的三种方法都能够优化车辆数量,在 最差的 PMX 实验中,也有 60% 达到了最佳车辆数量。 车辆固定成本惩罚点可以纳入自适应功能,以降低总体 成本并解决问题。
3 带硬时间窗车辆路径问题改进遗传算法
3.1 算法的设计
3.1.1 构造染色体,产生初始种群
3.1.2 确定适应度函数
遗传算法的一个特点是,它们只能通过仅应用给定 问题的目标函数来获得以下搜索信息,该函数保留在爬 山遗传算法中,目标函数的使用表示为个体适应评估。 过程如下 :
(1)对个体编码串进行解码处理后,可以得到个体 的表现性 ;
(2) 由个体的表现性可计算出对应个体的目标函数值;
(3)根据最优化问题的类型,由目标函数值按一定 的转换规则求出个体的适应度。
因此,对于目标函数为 Z 到搜索空间对应的个体适 应度函数可以取为如式(22)所示 :
3.1.3 选择操作
采用自适应比例法,该方法选择的个体大小取决
3.1.4 染色体的交叉重组
本文以局部映射交叉法(PMX)为例,基于 PC 交 叉概率进行交叉重组, PMX 的步骤如下 :(1) 随机选 择父代个体的交配区域 ;(2) 在配接区域中,随机选择 交叉点X 和 Y ;(3) 确定映射关系 ;(4) 根据映射关系 恢复非交换部分。
3.1.5 爬山操作
具体的爬山操作流程图如图 2 所示。
3.1.6 停止准则
确定迭代代数是否为给定代数,如果是, 则停止进 化 ;相反,循环则仍继续进行。
3.2 算法的应用及结果分析
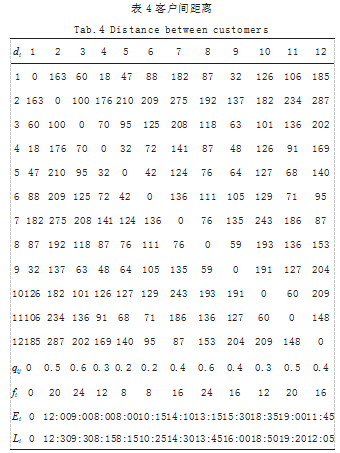
以某配送中心为例。目前,配送中心拥有 13 辆车, 40 个配送点位,包括两种车型。5 辆货车用于从上游供 应商批发货品,容量为 5t,最远行驶里程 800km。8 辆 商务车辆设计用于向零售和终端客户运输货品,负载能 力为 1.5t,车速为 40km/h(平均车速),最大运输距离 为 600km。目前,根据配送中心的实际情况,正在优化 下游县区市的配送路线,优化车辆行驶路线使总路线最 短。如表 4 所示为该中心仓库各客户之间的距离 dij (其 中客户 1 为配送中心)、各客户的药品需求量 qij(i, j=1. 2. 3. …, 11)(各客户的平均需求量)、各客户 服务时间fi 分钟、各客户货物需求时间窗 [Ei,Li]。
结合实际,种群规模取值 M=30.迭代次数 200. pc=0.7. pm=0.01. 基因变异时的换位次数为 5.爬山时 操作次数 20.不可行路径的惩罚权重为 800km, 以此 数据随机求解十次后,得到最优解 1190.3km。该最优解对应路线分别为 :(1)1-3-2-9-1 ;(2)1-4-6-10-8-1 ; (3)1-5-12-7-11-1.
4 结语
目前,电子商务的快速发展带动了快递业的发展, 影响快递服务质量的重要因素之一是快递的交货时间。 本文的目的是尽量减少快递服务的交付时间,并探索一 种具有时间窗口的运输方式。为了克服遗传算法收敛缓 慢和初始缺陷,开发并采用了基于分段交叉算子和延迟 时间的局部搜索策略。与简单的遗传算法相比,改进的 混合遗传算法在全球范围内具有优越的搜索能力,证明 了该算法的有效性。
参考文献
[1] 周景欣.遗传算法求解带时间窗的车辆路径问题[J].中国储 运,2023(1):100-101.
[2] 何小年.带软时间窗约束的多车场车辆路径问题及其禁忌搜 索算法研究[J].信息记录材料,2023.24(1):97-99+103.
[3] 赵家儒,谭代伦.改进遗传算法求解带时间窗的外卖配送车 辆路径规划[J].绵阳师范学院学报,2022.41(2):9-17.
[4] 胡小建,周琼,宋旭东,等.基于时间窗约束的多人多储位拣选 路径优化模型及改进遗传算法应用研究[J].计算机集成制造系 统,2022.28(11):3354-3364.
关注SCI论文创作发表,寻求SCI论文修改润色、SCI论文代发表等服务支撑,请锁定SCI论文网!
文章出自SCI论文网转载请注明出处:https://www.lunwensci.com/jisuanjilunwen/74008.html