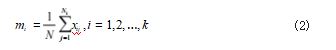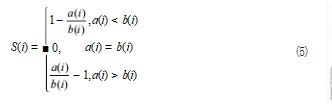SCI论文(www.lunwensci.com)
摘 要 :计算机网络技术日益成熟完善,大数据时代日新月异。每时每刻产生的大量数据信息也逐渐复杂,因此数据分析 也越来越受到广大学者的关注。而聚类分析是数据挖掘中划分和分组的重要方法之一,在生物、医疗、机器学习、市场营销等 诸多领域都得到广泛应用。K-means 聚类算法作为一种可扩展性、高效性的聚类算法,在解决大规模数据聚类处理问题时有着 独到的优势。基于此,该研究提出了一种针对 K-means 聚类算法肘点法中的先验性 K 值不准确的 K 值纠正优化算法。该算法 结合了 ISO-DATA 算法原理,实现了在先验性 K 值的一定范围内根据数据集的特征利用多参数实现 K 值更准确的选择。
Optimization Research of K-means ClusteringAlgorithm
HANYu1. WANG Qing2. LIU Li'na2
(1.Department of Artificial Intelligence,Jinhua Advanced Research Institute,Jinhua Zhejiang 321013;
2.School of Electronic and Information Engineering, Soochow University, Suzhou Jiangsu 215006)
【Abstract】:Computer network technology is becoming more and more mature, and the era of big data is changing. A large amount of data information generated at all times is gradually complex, so data analysis has attracted more and more attention . Clustering analysis is one of the important methods of partitioning and grouping in data mining, which is widely used in many fields such as biology, medicine, machine learning, marketing and so on. As a scalable and efficient clustering algorithm, K-means clustering algorithm has unique advantages in solving big data clustering problems. Based on the above, this study proposes a K value correction optimization algorithm for the inaccurate prior K value in the elbow method of K-means clustering algorithm. The algorithm combines the principle of ISO-DATA algorithm, and realizes more accurate selection of K value by using multiple parameters according to the characteristics of the data set within a certain range of the prior K value.
【Key words】:cluster analysis;K-means algorithm;ISO-DATA algorithm;elbow point method;parameter selection
数据挖掘是当前计算机研究的热点之一,而聚类分 析是数据挖掘中数据划分和数据分组的重要方法, 一直 以来受到众多研究者的关注,在生物学和医学、市场营 销、文本分类、机器学习等各个领域都得到广泛应用。
聚类分析是一种无监督机器学习方法,是指一组数 据对象,研究如何自动将数据对象划分到不同的聚类中, 让同一聚类的对象在某种程度上具有较高的相似度,而 不同聚类中的数据对象具有较低的相似度 [1]。
K-means 算法作为一种基于分区的聚类算法,算法复杂度很低,聚类效果优异。但是聚类结果随机性大, 易受其他因素的影响,例如,孤立点、初始聚类中心的 选取、K 值等。
为提高 K-means 算法聚类结果的稳定性和计算速度, 邹臣嵩等提出一种基于最大距离积与最小距离之和的协同 K 聚类改进算法 [2]。靳雁霞等提出了一种改进的简化均值 粒子群 K-means 优化聚类算法(ISMPSO-AKM) [3]。徐 慧君等提出一种改进的 Mini Batch K-means 时间权重 推荐算法 [4]。王义武等将空间投影应用于 K-means 算法中,准确度和计算时间方面都得到了大幅提升 [5]。
为消除传统 K-means 算法对孤立点及初始聚类中 心敏感问题,袁方等提出一种优化初始聚类中心的方法, 以提高聚类的效果 [6]。刘洋利用基于精英反向学习的萤 火虫寻找初始聚类中心,在一定程度上减少了聚类的迭 代次数 [7]。李艳等将粗糙集中的约简方法与 K-means 算 法相结合,提出一种基于多粒度聚类的属性约简方法 [8]。 马福明等发现新增数据点会导致类簇结构发生变化,提 出对类簇进行分裂或合并操作,让聚类中心自适应调整 [9]。
而在 K 值选择上,可以利用肘点法得到经验性 K 值,但“肘点”位置却不明确 [10]。贾瑞玉等重新定义 数据点的局部密度,通过残差分析自动确定类簇数目和 初始聚类中心,将新算法命名为 CNACS-K-means 算 法 [11]。王建仁等利用指数函数的指数爆炸性质, 改进 “肘点”值 [12]。王子龙等提出一种以维度加权的欧氏距 离计算样本的密度和权重的方法,它可以自动获取初始 聚类中心以及聚类数目。杨红等考虑到类间差异性,改 进准则函数,从而放大了聚类效果 [13]。
肘点法本质上是通过数据本身的轮廓系数的梯度选 择出肘点附近的 K 值,但是如果数据内聚度不大,或者 簇数过多时,往往不能选择出准确的 K 值。该研究提出 利用数据集之外的参数阈值来实现迭代,从而实现 K 值 修正,进而优化 K-means 算法。
1 相关知识
假设原始数据集X={x1.x2. … ,xn} 具有 n 个样本, K- means 算法将数据集划分为 K 个类,不能存在空的类 且各样本只有唯一归属。在每个类中各选择一个数据点 作为初始聚类中心。根据距离划分各个样本,把样本划 分到最近的类中。接着重复之前的过程,更新聚类中心 和样本到聚类中心点的距离,重新分配样本,直到聚类 中心不再发生变化,输出聚类结果。
以下是 K-means 算法具体流程 :
Step1 :确定分组数量 K ;
Step2 :随机选取 K 个点作为初始聚类中心 mi ;
Step3 :按照公式 (1) 计算各样本xi 到聚类中心的欧氏 距离,即 SSE(Sum of the Squared Errors,简称 SSE) :
Step4 :根据距离,把各样本划分到最近的聚类中 ;
Step5 :更新聚类中心 mi,如公式 (2) 所示 ;
其中 Ni 是隶属于第 i 个聚类的样本数量。
Step6 :判断聚类中心是否发生变化,若无变化,则 算法终止。否则,转回 step3.
由此可见, K-means 算法的特点是每次迭代都需 要重新判断各个样本是否被分配到正确的类中。如果分 类结果不满足要求,就进行修正,在所有样本分类修正 后,就认为各个样本被正确地划分到对应类中,再更新 聚类中心,开始新一次的迭代。
对于 K-means 算法,首先要注意的是 K 值的选择, 一般来说,研究者会根据对数据的先验经验选择一个合 适的 K 值。先验性 K 值的选择使用到肘点法,其核心指 标 SSE 见式 (2),其核心思想可以简要概括为随着聚类 数 K 的增大,样本划分会更加精细,每个簇的聚合程度 会逐渐提高,那么误差平方和 SSE 自然会逐渐变小。当 K 小于真实聚类数时,由于 K 的增大会大幅增加每个簇 的聚合程度,故 SSE 的下降幅度会很大,而当 K 到达真 实聚类数时,再增加 K 所得到的聚合程度回报会迅速变 小,所以 SSE 的下降幅度会骤减,然后随着 K 值的继续 增大而趋于平缓。这就会形成 SSE 图像会以真实的 K 值 为分界, 从陡峭变得平缓形成一个手肘的形状。但当数 据集的复杂度变大时,通过手肘法往往只能选择出一个 区间,无法准确地选择一个确切的值。
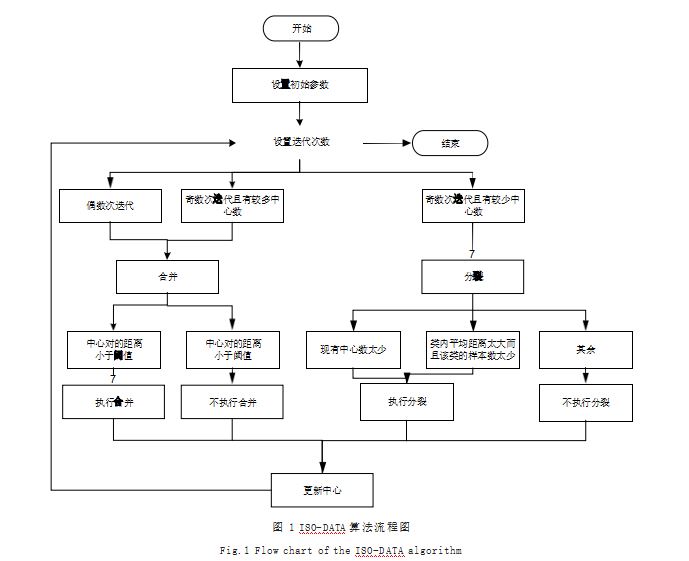
2 K-means 算法改进思路为修正 K 值,该研究使用到 ISO-DATA 算法,其 定义基本与 K-means 聚类算法相同,这里便不做赘述。 该算法的基本思路图如图 1 所示 :算法核心只有分裂、 合并和更新中心三个步骤,当目前的聚类数太少的时候 进行分裂,当聚类数过多则进行合并,如果是奇数次迭 代,尝试分裂,如果是偶数次迭代尝试合并,通过更新 中心选择出最佳的中心数目。
在流程图中, “合并”步骤并不一定执行了合并, 只有满足在所有的中心中,存在一些中心的距离低于了 设定的阈值才会真正地执行合并的操作,其余不执行合 并的操作。而在分裂中,只有现有的中心数太少或者满 足类内的距离太大而且样本数太少进行分裂的操作。其 中类内的距离太大则表示了这个聚类太过于松散,再加 上类的数量太少的话,才进行分裂。通过迭代,最终确 定出符合参数的 K 值,这属于一种多参数的 K 值选择。
为衡量聚类算法的准确性,该研究使用轮廓系数作 为衡量指标。轮廓系数计算公式如公式 (3) 所示 :
其中, a(i) 代表样本点的内聚度,如公式 (4) 所示 :
其中j 代表与样本 i 在同一个类内的其他样本点 ; a(i) 越小说明该类越紧密。
b(i) 的计算方式与 a(i) 类似,只不过需要遍历其他 类簇得到多个值 {b1(i),b(i)} 从中选择最小的值作为最终 的结果。
所以 S(i) 可分类为如公式 (5) 所示 :
由式 (5) 可以发现 :
当 a(i)
当 a(i)>b(i) 时,类内的距离大于类间距离,说明聚 类的结果很松散, S 的值会趋近于 -1.
由此可得 :轮廓系数 S 的取值范围为 [-1.1],轮廓
系数越大聚类效果越好。
3 实验结果
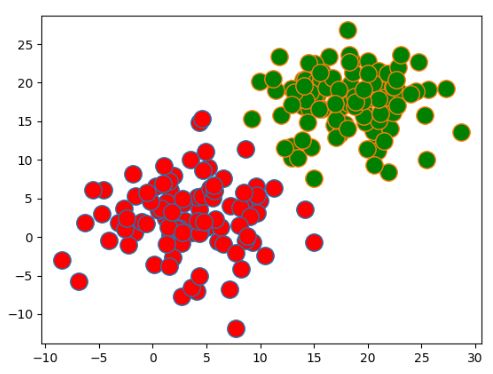
为验证优化算法是否能修正 K值,该研究使用 make_ blobs 函数产生数据集,按照 8 个数据中心,样本数为 50000 个产生数据集, 随机种子设置为 170.接着使用 肘点法得到先验的 K 值的区间,选取数值进行聚类 ;再利用改进算法对 K 值进行修正后,接着对数据进行聚类。 利用肘点法得到的轮廓系数图如图 2 所示。
图中肘点不明显,经验性 K 值区间为 [3.4] 或者 [6.8]。 按照 K=4 进行 K-means 聚类,结果如图 3 所示。可以 发现聚类结果中出现了孤立点,而且有边缘点被划分到 错误的类别中,这都是 K 值选取有误导致的。
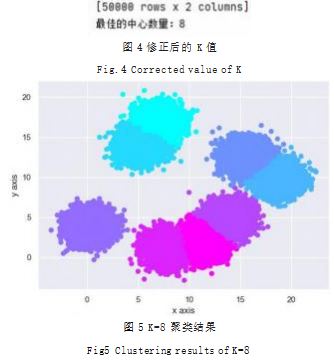
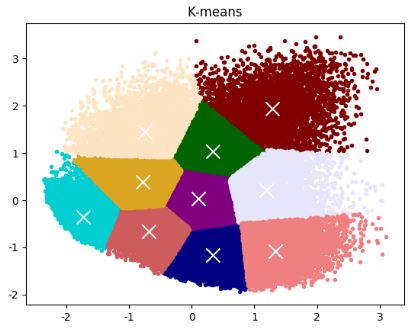
利用改进算法对 K 值进行纠正,如图 4 所示,修正 后 K 值为 8.修正后的 K 值聚类结果如图 5 所示。这 说明改进算法是比肘点法更为准确, 有效地找到了 K 值,验证了算法的准确性。
该研究提出了一种基于 K-means 的聚类优化算法,该算法将 ISO-DATA 聚类算法、K-means 聚类算法与 肘方法相结合,实现了 K 值的选择和多参数对 K 值的 修正,从而对 K-means 的先验性 K 值起到了修正作 用,提高了 K 值选择的准确性。通过实验仿真,可以发 现,优化算法能够为数据集提供更准确的 K 值,证明了 算法的可行性和准确性。
未来的研究可以从以下两方面展开 :
(1)进一步探究算法的具体参数,例如主要参数阈 值与数据的特征值之间的最佳关系。
(2)对于随机程度较大的数据集,本算法往往无法 准确纠正 K 值,因此需要更多的实验数据以改进算法。
参考文献
[1] KANUNGO T,MOUNT D M,NETANYAHU N S,et al.An Efficient K-means Clustering Algorithm:Analysis and Implementation[J].IEEE Transactions on Pattern Analysis & Machine Intelligence,2002.24(7):881-892.
[2] 邹臣嵩,杨宇.基于最大距离积与最小距离和协同K聚类算法 [J].计算机应用与软件,2018.35(5):297-301+327.
[3] 靳雁霞,齐欣,张晋瑞,等.一种改进的简化均值粒子群K-means 聚类算法[J].微电子学与计算机,2020.37(5):69-74.
[4] 徐慧君,王忠,马丽萍,等.改进Mini Batch K-Means时间权 重推荐算法[J].计算机工程,2020.46(3):73-78+86.
[5] 王义武,杨余旺.空间投影在K-means算法中的研究与应用 [J].计算机工程与应用,2020.56(7):200-204.
[6] 袁方,周志勇,宋鑫.初始聚类中心优化的K-means算法[J]. 计算机工程,2007(3):65-66.
[7] 刘洋,王慧琴,张小红.结合蚁群算法的改进粗糙K均值聚类 算法[J].数据采集与处理,2019.34(2):341-348.
[8] 李艳,范斌,郭劼,等.基于K-原型聚类和粗糙集的属性约简方 法[J].计算机科学,2021.48(增刊1):342-348.
[9] 马福民,孙静勇,张腾飞.考虑边界样本邻域归属信息的粗糙 K-means增量聚类算法[J].控制与决策,2022.37(11):2968-2976.
[10] REZAEE M R,LELIEVELDT B P,REIBER J H.A New Cluster Validity Index for the Fuzzy C-means[J].Pattern Recognition Letters,1998.19(3/4):237-246.
[11] 贾瑞玉,李玉功.类簇数目和初始中心点自确定的K-means 算法[J].计算机工程与应用,2018.54(7):152-158.
[12] 王建仁,马鑫,段刚龙.改进的K-means聚类K值选择算法 [J].计算机工程与应用,2019.55(8):27-33.
[13] 王子龙,李进,宋亚飞.基于距离和权重改进的K-means算 法[J].计算机工程与应用,2020.56(23):87-94.
关注SCI论文创作发表,寻求SCI论文修改润色、SCI论文代发表等服务支撑,请锁定SCI论文网!
文章出自SCI论文网转载请注明出处:https://www.lunwensci.com/jisuanjilunwen/73541.html