一种基于曲面拟合的图像压缩方法论文

SCI论文（www.lunwensci.com）

　　摘 要 ：针对使用固定大小图像块和固定模型的曲面拟合图像压缩方法存在的还原图像质量问题,提出了一种多层次多模 型的图像数据拟合算法,即首先依据图像区域的平坦度对图像进行多层级的错位分块,然后进一步依据分块的数据平坦度选择 不同模型拟合达到压缩数据的目的 ;在图像还原时,依据分块之间的错位信息进行边界融合,较好消除了分块间的拼接痕迹, 有效提高了还原后的图像质量。本文所提算法与经典的多项式拟合算法、标准图像压缩算法(JPEG)以及 JPEG2000 算法实验 对比分析,本文算法有效提高了图像的压缩比,较好消除了还原图像的块效应,且在相同峰值信噪比下,所提算法图像质量与 结构相似性指数高于 JPEG 和 JPEG2000 算法。

　　【Abstract】：A multi-level, multi-model image data fitting algorithm is proposed to address the issue of image quality in the existing image compression methods that use fixed-size image blocks and fixed models for surface fitting. Firstly, the image is divided into multiple hierarchical displaced blocks based on the flatness of image regions. Then, different models are selected for fitting the blocks based on their data flatness, aiming to achieve data compression. During image reconstruction, boundary fusion is performed using the displacement information between blocks, effectively reducing artifacts at block boundaries and improving the quality of the reconstructed image. The proposed algorithm is compared and analyzed against classical polynomial fitting algorithms, standard image compression algorithms, and JPEG2000. The results show that the proposed algorithm achieves improved compression ratio, effectively mitigates block artifacts in the reconstructed image, and exhibits higher image quality and structural similarity index compared to JPEG and JPEG2000 algorithms under the same peak signal-to-noise ratio.

　　【Key words】：image compression;surface fitting;block effects;misaligned chunking;flatness judgments

　　0 引言

　　图像压缩一直是计算机应用领域的重要研究方向, 特别是随着图像传感器技术的发展,从各类成像设备中 所能获得的图像分辨率越来越高,图像数据量也就越来 越大,高分辨率的图像虽然能够较好地满足相关应用的 需求,但其在传输和存储上的花销也就越来越大。如何 能用较小的空间成本获得较高分辨率和品质的图像便是 图像压缩领域的重要课题。在图像压缩领域,人们通过几十年的研究,分别提出了基于 DCT 变换的 JPEG 标 准和基于 DWT 变换的 JPEG2000 标准等,并且这些标 准都分别在不同领域得到了广泛应用 [1]。然而,随着各 类成像设备所获得的图像分辨率越来越高,图像数据量 越来越大,能否探索出一种能用更小空间成本来存储更 高分辨率和品质的图像压缩方法一直也是广大学者所追 求的目标 [2]。正因为如此,近十几年,人们在如何利用 曲面拟合方法实现图像压缩方面开展了不少研究,并取得了一定效果 [3-8]。

　　基于曲面拟合的图像压缩算法,它本质上是将图像 颜色值转换为简单的数学方程(线性或非线性),进而 通过数学方程系数代替图像颜色值来表征和保存图像信 息来达到图像压缩之目的。而这种拟合往往又是先将图 像分割成像素块来进行,例如,文献 [9] 通过平面拟合 进行图像压缩,文献 [10] 使用基于块的曲面三角剖分的 分段线性图像编码,文献 [11] 使用基于曲线特征驱动的 细分曲面创建和表示图像等。

　　依据基于曲面拟合图像压缩的机理不难发现,该压 缩方法在处理有明显几何结构或表面特征的图像时往往 会表现较好,例如,地理信息或医疗图像等,可以有效 提高压缩图像的保真度,并且在高压缩比下将产生较少 的质量损失和压缩伪影 [12]。然而,由于基于曲面拟合的 图像压缩方法往往是基于图像块来实现,势必就会在图 像重构时产生块间过度突兀的块效应,目前,虽然有些 文献通过引入一些较为复杂或计算量较大的预处理或后 处理来消除块效应,但效果并不理想 [11.17]。正因如此, 本文设计了一种多层次多模型的图像数据拟合算法,旨 在改进图像的分割方法以及消除重建图像的块效应问题, 并充分考虑并利用图像像素之间的相关性来灵活的选取 拟合函数,进一步提高图像的压缩比。与以往的工作相 比,本文所提算法在较小计算量和复杂度下较好地改善 了块效应问题并且进一步提高了图像的压缩比和质量。

　　1 相关工作

　　依据基于曲面拟合图像压缩的机理不难发现,该压 缩方法在处理有明显几何结构或表面特征的图像时往往 会表现较好,正因为如此,目前,基于曲面拟合的图像 压缩方法已经在不少应用领域应用并取得了不俗的效 果。例如,在文献 [13] 中介绍了基于曲面拟合的图像 压缩方法在无线多媒体传感器网络中的应用,其效果优 于基于 DCT 和 DWT 的图像压缩方法。而在文献 [14] 中则提出了利用 Savitzky-Golay 平滑滤波器和曲面拟 合模型进行高光谱图像压缩的方法,效果比使用 DCT、 DWT 和 PCA 更好。同样, Wang 等人在文献 [15] 中提 出一种基于自适应分类的曲线拟合算法,高效的压缩了 干涉多光谱图像, 较好地解决了使用 JPEG2000 对干涉 多光谱图像压缩时所产生的数据分析不足问题。

　　然而就目前的研究工作而言,其大部分工作都集中 在拟合曲线(面)模型的选择和块间融合方面。例如, Shaimaa M. Othman 等人提出一种利用多项式曲线拟 合实现图像压缩的方法,并分析得出使用 8 阶像素块分 割时获得的效果最佳 [16]。Ameer 和 Basir 则首先将图像划分为不重叠的块,然后引入一种平面拟合实现可伸 缩的图像压缩,在此基础上采用简单的量化和编码方案 以降低成本 [17]。Sajikumar 和 Anilkumar 提出了用于 图像压缩的二元多项式表面拟合方法,即使用第一类切 比雪夫多项式生成每个块的曲面,而块的大小由预定义 确定 [18]。Al-Bahadili 则提出了一种基于像素块方差值 来选择两个自适应多项式拟合进行图像压缩方法,并结 合均匀量化器和霍夫曼编码实现图像压缩 [19]。Butt 和 Sattar 提出了一种用于图像压缩的曲线拟合模型, 研究 探讨了在不同阶像素块上使用不同阶曲线拟合,实验表 明,在相同曲线拟合函数下,使用较小像素块可以获得 更好的图像质量,但压缩比较低 [20]。Walaa Khalaf等 人提出了利用双曲函数增强曲面拟合图像压缩的方法,该 方法加强图像的边缘,消除遮挡效应,提高结构相似性指 数,对重建图像的客观和主观质量有着显著的提高 [21]。 以上研究分别从不同视角或用不同模型对图像像素值进 行了数学模型化,并取得了较好压缩效果,然而上述研 究并没有充分利用图像不同部分之间的信息相关性,这 在一定程度上影响了其最终的压缩效果。

　　由于使用曲面拟合的图像压缩方法都是基于图像块 来实现,在较高的压缩比下重建图像时通常会产生较为 严重的块间效应,进而影响了图像的再现品质。正因为 如此,在一些研究工作中提出增加预处理或后处理方法 来减少块间效应。例如, Zhou 和 Zheng 等人提出了 一种基于细分的矢量图形的图像表示和创建,图形表示 是由三角形网格定义的细分曲面,在顶点处添加颜色属 性,在边处添加特征属性,在此基础上引入了一种特殊 的三次 b 样条来描述图像的曲线特征,有效地处理具有 复杂边界或特征的图像并且能够忠实地重建曲线特征, 较好改善了块间效应 [11]。Ameer 和 Basir 则在解码器 上,引入一阶曲线拟合块边界的四个像素值,以找到更 好的估计边界像素来弱化块间效应 [14]。虽然上述方法 可以较好地消除了块效应和伪影,但其有着较大的计算 量和复杂度。

　　2 多层次多模型的图像数据拟合方法

　　对于不同的图像, 若按相同的大小进行分割, 其不 同块内块间的空间相关度是不同的,而如何利用图像不 同部分之间的信息相关性是获取高压缩比的关键。对图 像采取多层次分割,可提高像素块对空间相关性的契合 度,进而为提高压缩比提供可能。其中的关键是如何判 断空间相关性?本文引入像素块平坦度判断方法。

　　2.1 多层次图像分割

　　对图像多层次分割获取的不同阶数像素块采取平坦

　　其中f(x,y) 为原像素块像素点的值, N 为像素块阶 数 ;指定阈值 s,当 S ≤ s 时,则认定像素块平坦。对 于不同阶数的像素块,其阈值 s 是不同的。

　　由于人眼对色度信号的敏感程度比对亮度信号的敏 感程度低,利用这个特性可以去除图像中一部分颜色信 息。因此,实验将 RGB 图像转换为 YCbCr 图像,并 分离出 Y, Cb, Cr 三个通道。对于 Y, Cb, Cr 三个通 道进行有差别处理。对于亮度通道 Y,设置严格阈值 s。 对于颜色通道 Cb, Cr,设置宽松阈值 s。对于不同通 道及不同阶级像素块,其阈值也是不同的。本文所提 算法阈值设定为 ：sY4=50. sY8=30. sY16=10. sCbCr4=100. sCbCr8=70. sCbCr16=40. 例如, sY4=50 表示 Y 通道 4 阶像 素块的平坦判断阈值为 50. sCbCr4=100 表示 CB 和 CR 通道 4 阶像素块的平坦判断阈值为 100.

　　3 拟合函数选取

　　3.1 平面拟合

　　本文对于各阶平坦像素块, 采用平面拟合,保存像 素块大小及平均值,以较少的参数进一步提高图像压缩 比。具体而言,平坦像素块通常表示图像中比较平滑的 区域,如天空、水面等,这些区域内的像素值变化较 小,可以用一个平面函数进行拟合。平面拟合函数定义 如式(3)所示 ：

　　3.2 双曲正切函数拟合

　　本文对于四阶非平坦像素块采取一种双曲正切函数 拟合。非平坦像素块通常表示图像中的边缘、纹理等区 域,这些区域中的像素值变化较为复杂,需要用更复杂 的函数进行拟合。双曲正切函数是一种非线性函数,可以较好地拟合这些复杂的像素块,并且该函数对重建图 像的主客观质量有着显著的提高 [21]。双曲正切函数定 义如式(4)所示 ：

　　对于双曲正切函数来说, a 是像素块的基本值(最 小值), b 是增长参数, c 和 d 则控制着块中的边缘方向。 当系数 c 和 d 较大时,边缘方向变化缓慢,式 (5) 中的 条件是实现可感知的方向变化, tanh 函数的最大值为 0.964 (tanh (2)), 在 N×N 像素块的端角。这种情况将 缩小这些系数的值,并将系数的数量减少到 3.因此, 这将增加压缩比(CR)。

　　4 面向多层次图像分块的块效应消除方法

　　图像压缩中基于曲面拟合的方法在实现高压缩比的 同时,会出现块效应的问题。这是由于在压缩过程中, 像素被分块处理,每个像素块被曲面拟合并压缩成一个 单独的数据单元。当进行图像还原时,这些数据单元被 重新拼接成像素块,由于拟合曲面的复杂度有限,导致 块与块之间的边界不够平滑,从而产生了明显的块效应。

　　本文提出一种错位分块的方法。错位分块方法将使 得对于一般的像素块,其周边像素与其相邻像素块周边 像素相同,增加其与周边像素块的相关性。在进行曲面 拟合之后,该像素块拟合出来的曲面将与相邻像素块拟 合出来的曲面具有一定的连续性。图像还原时依据分 块之间的错位信息进行边界融合(块边界取其平均值), 从而使得还原出来的图像边界基本达到平滑过渡的效 果,继而解决了块效应的问题。

　　在图像多层次分块之前, 首先将其像素矩阵以 3 为 倍数进行行和列的复制扩充(像素矩阵首行首列下标为 0 ;例如, 扩充后 512×512 像素图像变为 682×682 像 素图像)。这样在进行非重叠分块时,各阶像素块就能 够实现错位分块的效果(最小为四阶)。在图像还原时, 依据分块之间的错位信息进行边界融合,消除因图像扩 充所产生的行和列。

　　假设原图像 I 的大小为 M×N,对其进行行和列的 扩充后得 M '×N ' ;再进行多层次分块,每个像素块大 小分别为 B1.B2. … ,Bl,其中 B1 ≤ B2 ≤ … ≤ Bl。为实现 像素块的均等分割,分块前将 M '×N ' 的像素矩阵进一 步扩充为 ceil(M '/Bl)×Bl ×ceil(N'/Bl)×Bl 的矩阵 I ',其 中 ceil(X) 表示X 向上取整。扩充方式以尾行尾列进行 复制扩充(图像还原时消除)。

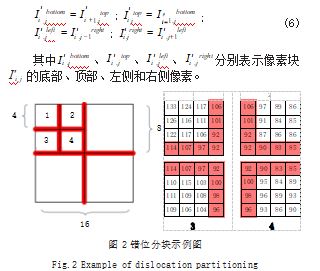
　　令 I 'i,j 表示 I ' 中第 i 行第j 列的像素块,其错位分块方式可以表示为如式(6)所示 ：

　　如图 2 所示中红色阴影部分为块错位部分像素, 8 阶和 16 阶像素块与之相似。边界融合时,错位部分像 素取其平均值。

　　5 实验结果与性能分析

　　本节中,将通过压缩比、均方误差、峰值信噪比 和结构相似性指数来讨论所提出算法的性能,即 CR、 MSE、PSNR 和 SSIM。本文所提算法将与多项式拟合 图像压缩算法、文献 [21] 中所提算法、JPEG 算法以 及 JPEG2000 算法进行对比,继而凸显本文所提算法 的优越性。本文选取实验图像为 LENA(雷安娜)图、 PEPPER(胡椒)图、HOUSE(房子)图和 SPLASH 图(溅上的液体),四图均为 512×512 像素。

　　其中 μx 为 x 的平均值, μy 为y 的平均值, σx2 为 x 的方差, σy2 为y 的方差, σxy 为 x 和y 的协方差, c1 和 c2 为常数。

　　5.1 多项式拟合实验

　　首先,对图像采用经典的多项式拟合实验。在多项 式拟合方法中,我们将一个图像分割成 4×4、8×8 或 16×16 的不重叠像素块, 然后采取多项式拟合压缩图 像。拟合函数一般有一阶多项式函数、二阶多项式函数 以及高阶多项式函数,综合考虑图像质量以及图像压缩 比,本文选取二阶多项式进行实验(多项式阶数越高, 图像质量越好,压缩比越低)。为方便进行方法间的对 比,实验均不采取量化和编码操作。

　　二阶多项式函数定义如式(11)所示 ：

　　为凸显多层次分块的优势,采取以下实验 ：

　　(1)将图像分割为四阶、八阶、十六阶的不重叠像 素块,采取二阶多项式拟合 ;

　　(2)对图像进行多层次分割,平坦像素块采取平面 拟合,非平坦像素块采取二阶多项式拟合。

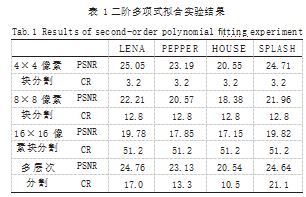
　　多项式拟合实验结果图如图 4 所示, 二阶多项式拟 合实验结果如表 1 所示。

　　从图 4 和表 1 数据分析对比,可以很明显地观察到 随着分割像素块大小的提高,图像质量逐步下降、压缩 比逐步提高以及愈发严重的块效应。结合以上三种分块 方式的优缺点,多层次分块充分利用了不同块内块间的 空间相关性,保证图像高压缩比的同时也兼顾图像的高 质量 ;其与使用四阶像素块分割的方法相比,压缩图像平均 PSNR 仅降低 0.07db, 平均 CR 却提高了 12.23. 并且有着使用四阶像素块分割方法相近的主观质量 ;与 使用八阶像素块分割的方法相比,平均 PSNR 提高了 2.49db,平均 CR 提高了 2.68.并有着远高于使用八 阶像素块分割方法的主观质量 ;与使用十六阶像素块分 割的方法相比,尽管后者有着更高的压缩比,但其主观 上,图像的结构和细节受到了极大的破坏和扭曲,导致 了不能接受的视觉体验。以上实验充分表明了多层次分 块的优越性能。

　　虽然多层次分块方法提高了图像的质量与压缩比, 但其产生的块效应依然无法避免。因此,对该方法采取 错位分块以消除块效应,进一步提高图像质量。

　　如图 5 和表 2 所示,根据数据分析对比,可以发现图像错位分块处理后,其 PSNR 和主观质量有了明显的提高 (平均 PSNR 提高了 3.35db),压缩图像显得更加的平滑, 其所产生的块效应也大幅度减少 ;并且由于采取错位分块 方法时增加了大量的像素值,这使得压缩图像的压缩比大 大降低。但该方法有效地处理了多层次分块所产生的块效 应问题 ;就目前业界学者所采取消除块效应的预处理或后 处理操作与本文方法对比, 前者计算及方法实现上更加复 杂一些,且大多适用于处理分割为固定块大小的图像。

　　5.2 本文所提算法实验

　　本文所提算法采取文献 [21] 中双曲正切函数拟合多 层次分块中的四阶非平坦像素块,该函数对划分为四阶 像素块拟合的图像在还原时有着较好的主客观质量,并 在一定程度上消除块效应。

　　实验首先复现了文献 [21] 中的图像压缩方法,然后 与本文所提算法进行对比。

　　从图 5、图 6、图 7 和表 3 数据对比来看,在本文所 提算法下重建图像的主观质量较文献 [21] 中算法重建图 像有着一个明显的提升,并且在文献 [21] 中算法重建图 像的基础上进一步消除了图像的块效应,使得块边界更 加的平滑。在客观质量上,所提算法的 PSNR 略高于文 献 [21] 中算法(平均 PSNR 提高 1.6db),并且所提算 法大大提高了图像的压缩比,且较文献 [21] 中算法相比, 平均 CR 提高了 6.3.再者,本文所提算法较多层次分割(错位分块)方法对比,前者主客观质量都优于后者并进 一步提高图像压缩比,体现出双曲正切函数的优良性能。 综上得出, 所提算法在压缩图像的主客观质量上都有很 好的特性。

　　5.3 对比 JPEG 和 JPEG2000

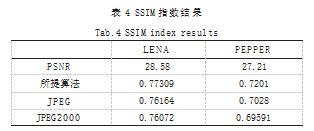
　　为了证明本文所提算法的优越性,实验与 JPEG 和 JPEG2000 进行对比。对比中,为更好地对比三者之间 的差距,本文引入结构相似性指数进行对比。结构相 似度指数(SSIM)测量了重建图像与原始图像的结构 变化范围。其值范围在 0.0 ～ 1.0 之间,值越大,表示 结构变化越小,反之亦然。本文 SSIM 采取三通道平均 值。如图 8 和表 4 所示显示了本文所提算法、JPEG 和 JPEG2000 对相同目标质量(PSNR)的结果图和 SSIM 结果,以 LENA 图与 PEPPER 图为例。

　　从表 4 中可以观察到所提算法与JPEG 和JPEG2000 相比,有着较好的 SSIM结果,尽管它们有着相同的 PSNR。 但是JPEG 和JPEG2000 的压缩比要高于所提算法,这 是因为它们使用了量化和编码,完成了大量的 CR。

　　如图 9 所示显示了本文所提算法、JPEG 和JPEG2000 的图像放大(×2)示例(同 PSNR 下)。结果表明,对 于同一 PSNR,所提算法与 JPEG 相比,该方法的图像 特征得到了很好的保存,有着较好的主观质量且大大降 低了阻塞效应 ;与 JPEG2000 相比,所提算法图像比 JPEG2000 更加清晰真实,更好地保留了图像的细节。

　　6 结论

　　本文提出了一种基于多层次多模型的图像数据拟合 的有损图像压缩方法。该方法利用分块图像不同块内块 间的空间相关性,对图像进行多层次分割,提高像素块 对空间相关性的契合度 ;采用多模型拟合多层次像素 块,以便于更好地适应不同的图像纹理特征和像素分布 情况,从而提高压缩效率和保留图像细节信息的能力。 并且本文所采取的面向多层次图像分块的块效应消除方 法,在较小计算复杂度下提高图像的精度和质量。

　　综上实验分析,可以得出结论, 本文所提算法比经 典的多项式拟合算法在兼顾图像质量的同时提供了更高 的图像压缩能力 ;与文献 [21] 中所提算法相比,本文所 提算法进一步提高了图像的压缩比以及大幅度消除了块

　　效应问题,使得重建图像更加的平滑 ;并且对于相同的 PSNR,在本文所提算法下的重建图像的纹理描述和主 客观质量与 JPEG 以及 JPEG2000 相比更加令人满意。

　　参考文献

　　[1] SINGH A,KIRAR K G.Review of Image Compression Techniques[C]//2017 International Conference on Recent Innovations in Signal Processing and Embedded Systems (RISE).Bhopal:IEEE,2017:172-174.
　　[2] HUANG C C,NGUYEN T P,LAI C T.Multi-channel Multi-loss Deep Learning Based Compression Model for Color Images[C]//2019 IEEE International Conference on Image Processing (ICIP).Taipei: IEEE,2019:4524-4528.
　　[3] BEITOLLAHI M,HOSSEINI S A.Using Curve Fitting for Spectral Reflectance Curves Intervals in Order to Hyperspectral Data Compression[C]//2016 10th International Symposium on Communication Systems, Networks and Digital Signal Processing (CSNDSP). Prague:IEEE,2016:1-5.
　　[4] ZHANG Y,WANG H,ZHAO J Y.Depth Map Compression Based on Platelet Coding and Quadratic Curve Fitting[C]// 2014 IEEE 27th Canadian Conference on Electrical and Computer Engineering (CCECE).Toronto:IEEE,2014:1-4.
　　[5] RONGCHUN S,DIANREN C,XINGGUANG L,et al.A Remote Sensing Image Compression Algorithm Based on Adaptive Threshold[C]//2009 Third International Symposium on Intelligent Information Technology Application Workshops.Nanchang:IEEE,2009:376-378.
　　[6] HOSSEINI S A,GHASSEMIAN H.A New Approach to Hyperspectral Data Compression Using Rational Function Approximation for Spectral Response Curve Fitting[C]//7'th International Symposium on Telecommunications(IST'2014). Tehran:IEEE,2014:844-848.
　　[7] SADANANDAN S,GOVINDAN V K.Image Compression with Modified Skipline Encoding and Curve Fitting[J]. International Journal of Computer Applications,2013. 74(5).
　　[8] LIU Y G,PENG S H.A New Image Compression Algorithm Base on Rotating Mapping and Curve Fitting[C]//2014 12th International Conference on Signal Processing (ICSP).Hangzhou:IEEE,2014:934-937.
　　[9] WATANABE T.Picture Coding Employing B‐spline Surfaces with Multiple Vertices[J].Electronics and Communications in Japan (Part I:Communications), 1997.80(2):55-65.
　　[10] LU T,LE Z,YUN D Y Y.Piecewise Linear Image Coding Using Surface Triangulation and Geometric Compression[C]// Proceedings DCC 2000.Data Compression Conference.Snowbird:IEEE,2000:410-419.
　　[11] ZHOU H,ZHENG J,WEI L.Representing Images Using Curvilinear Feature Driven Subdivision Surfaces[J].IEEE transactions on image processing,2014.23(8):3268-3280.
　　[12] ANANDAN P,SABEENIAN R S.Curvelet Based Image Compression Using Support Vector Machine and Core Vector Machine-A Review[J].International Journal of Advanced Computer Research,2014.4(15):675-681.
　　[13] BANERJEE R,BIT S D.An Energy Efficient Image Compression Scheme for Wireless Multimedia Sensor Network Using Curve Fitting Technique[J].Wireless Networks,2017.25(3):1-17.
　　[14] BEITOLLAHI M,HOSSEINI S A.Using Savitsky-golay Smoothing Filter in Hyperspectral Data Compression by Curve Fitting[C]//Electrical Engineering (ICEE),Iranian Conference on.Mashhad:IEEE,2018:452-457.
　　[15] 王柯俨,李云松,吴成柯,等.基于自适应分类曲线拟合的干涉多光谱图像压缩[J].光学学报,2009.29(1):78-85.
　　[16] OTHMAN S M,MOHAMED A E,NOSSAIR Z,et al. Image Compression Using Polynomial Fitting[C]// 2019 3rd International Conference on Electronics, Communication and Aerospace Technology (ICECA). Coimbatore:IEEE,2019:344-349.
　　[17] AMEER S,BASIR O.Image Compression Using Plane Fitting with Inter-block Prediction[J].Image and Vision Computing,2009.27(4):385-390.
　　[18] SAJIKUMAR S,ANILKUMAR A K.Image Compression Using Chebyshev Polynomial Surface Fit[J].Int.J.Pure Appl.Math.Sci,2017.10:15-27.
　　[19] AL-BAHADILI R J S.Adaptive Polynomial Fitting for Image Compression Based on Variance of Block Pixels[J].Engineering and Technology Journal,2015.33(8 Part (A) Engineering).
　　[20] BUTT A M,SATTAR R A.On Image Compression Using Curve Fitting[J].2010.
　　[21] KHALAF W,ZAGHAR D,HASHIM N.Enhancement of Curve-fitting Image Compression Using Hyperbolic Function[J].Symmetry,2019.11(2):291.

 
关注SCI论文创作发表，寻求SCI论文修改润色、SCI论文代发表等服务支撑，请锁定SCI论文网！

文章出自SCI论文网转载请注明出处：https://www.lunwensci.com/jisuanjilunwen/68795.html