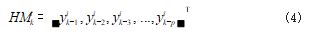SCI论文(www.lunwensci.com)
摘 要:本文针对发动机及控制系统并发故障的情况,设计一种基于决策级融合的单传感器自调整预测模型,提出一种基 于数据驱动算法 Meta-OSELM,用于构造发动机传感器的解析余度。并考虑多传感器发生故障时,基于信号融合传感器解析 余度算法失效问题,设计一种基于决策级融合的自调整预测模型,实现涡扇发动机的传感器自调整预测,并进行发动机及控制 系统并发故障下的故障监测与诊断验证。
Research on Monitoring Methods for Engine and Control System Status
CHEN Qianjing1. JIN Peng2. WANG Yawei2. PENG Ruixuan1. LU Feng2
(1. China Aeroengine Research Institute, Beijing 101399;2.State Key Laboratory of Mechanics and Control for
Aerospace Structural, Nanjing University of Aeronautics and Astronautics, Nanjing Jiangsu 210016)
【Abstract】: This article designs a single sensor self tuning prediction model based on decision level fusion for concurrent faults in engines and control systems, and proposes a data-driven algorithm Meta-OSELM for constructing analytical redundancy of engine sensors. And considering the problem of signal fusion sensor analysis redundancy algorithm failure when multiple sensors fail, a self adjusting prediction model based on decision level fusion is designed to achieve sensor self adjusting prediction for turbofan engines, and fault monitoring and diagnosis verification under concurrent faults in the engine and control system are carried out.
【Key words】: engine control system;fault monitoring;analytical redundancy;Meta-OSELM
0 引言
在航空发动机及控制系统单故障隔离方法中,传感 器故障隔离和定位对能否进行气路故障诊断来说至关 重要。基于模型的传感器故障诊断方法,主要分为三 种 :状态估计法 [1]、参数估计法 [2] 和等价空间法 [3],通 常需要计算量测参数与模型输出之间的残差信号,并且 确定阈值,根据一定的决策规则分析阈值和残差信号 的关系,判断故障是否存在并对故障进行定位。与此同 时,虽然同时发生两个或两个以上的多重传感器故障 的概率比较低,但对发动机控制与故障诊断系统可靠性 要求很高。为了进一步加强控制系统的可靠性,有必 要考虑到部件、执行机构以及多重传感器的并发故障 情况。
1 基于信号融合传感器解析余度方法
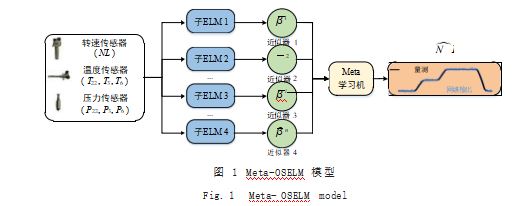
元学习是一种综合多种学习结果的通用技术,可以 大致定义为从学习者生成的信息中学习 [4]。本节提出一 种基于数据驱动算法 Meta-OSELM,用于构造发动机 传感器的解析余度 [5]。Meta-OSELM 模型是通过包括 子 ELM 单元和元学习器的基本配置实现,元学习器从 子 ELM 单元的输出中学习。高压转子转速参数的估计 值对应的元学习模型如图 1 所示。
每个子 ELM 单元为非线性拟合单元,元学习器为一 个单元拟合器,由一个监督 OSELM 组成。Meta-OSELM 为训练具有 ELM 隐藏节点的 OSELM 网络。每个子 ELM 单元利用数据集的不相交子集进行训练,然后在 整个数据集上训练监督 OSELM。元 OSELM 模型的最小化目标函数如式(1)所示 :
min : Lmeta −oselm = βk 2 +Emain ,k βk − Tk 2
其中 βk 为 k 时刻主 OSELM 网络的权值, βk = [βk1 ... βki ... βkn ]T , Tk = [tkmain,1 , ..., tkmain ,N0 ]T Emain ,k 是 k时刻由 n 个子 ELM 的输出组成,记为如式(2)所示 :
Emain ,k = [ELM1 (xk ) ... ELMi (xk ) ... ELMn (xk )]T
ELMi (xk ) = [gi (w1xk + b1 ) ... gi (wl xk + bb )]N1 *l * ■||βb1se ,i ■|| (2)|■βblase ,i ■|l *1
其 中 ELMi (xk ) 为 第 i 个 子 ELM 对 应 xk 的 输 出, gi ( ) 为第 i 个子 ELM 的隐含层非线性函数, βbase ,i 为第 i 个子 ELM 的隐含层的输出权值, βil,base 为第 i 个子 ELM中第 l 个输出权值。
Meta-OSELM 算法通过两阶段学习过程进行更新。 在第 1 阶段,初始数据被划分为 n 个不相交的子集,并 且利用子训练集离线训练子 ELM 单元。在第 2 阶段, 监督 OSELM 与第 1 阶段训练后的子 ELM 单元一起在 线训练。Meta-OSELM 算法如下 :
(1)Stage 1 ( 离线 ) :
第 i 个子 ELM 单元从Si 中计算βbase ,iendStep 3: 计算隐藏层输出矩阵Emain,0forj=1: l doEmain,0 (i, j) = ELMi (xj ) = gi (xj ) ⋅ βbase ,iendStep 4: 计算初始输出层权值β0
(2) Stage 2 ( 在线 )
输入 :ℵk = {(xi , ti )xi ∈ Rd ,ti ∈ R}// 新接收数据 输出 :βk+1 // 输出权值向量
Step 5: 计算隐藏层输出矩阵Emain ,k+1
Step 6: 更新输出权重Pk +1 , βk+1
2 发动机及控制系统故障监测系统仿真验证
当多传感器发生故障时,基于信号融合传感器解析 余度算法失效,因此本节调整了上节中的解析余度算 法,设计基于决策级融合的自调整预测模型,实现涡扇 发动机的传感器自调整预测,并进行发动机及控制系统 并发故障下的故障诊断验证。
2.1 基于决策级融合的自调整预测模型
用p 维的历史访问深度矩阵HMk(i)内的传感器信号 作为网络输入,如式(4)所示 :
其中, yk(i)表示 k 时刻的传感器 i 对应的信号,令预测向量作为神经网络输出。
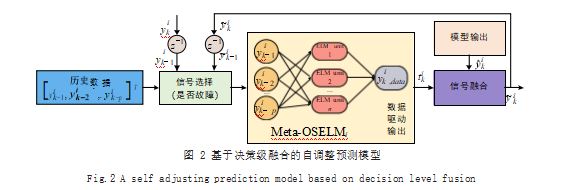
如图 2 所示,对于HMk(i)更新需要根据传感器是否故障进行信号选择,通过信号选择模块,尽可能保证信 号可靠。由第二节可知,首先根据接收的 k 时刻量测信 号进行控制系统故障诊断。若不存在传感器故障,那么 将利用其真实的量测信号更新下一时刻的历史数据 ;相 反,若诊断出传感器 i 发生故障,由于其故障信号不可 靠,因此需要对该传感器进行信号重构。传感器 i 对应的 Meta-OSLEMi 网络的输入HMk(i),基于数据驱动方法输出为 tk(i)。对于故障传感器信号重构部分,由第二节可知,通过融合决策级信号tk(i)与模型输出信号k(i) 计算出精度更高的融合结果k(i)。当前时刻k(i)和量测 yk(i) 用于下一时刻HMk(i)的更新。
NH本节在如图 3 所示的控制系统多重故障的基础上增加了轻度、中度、严重三种不同气路突变故障。
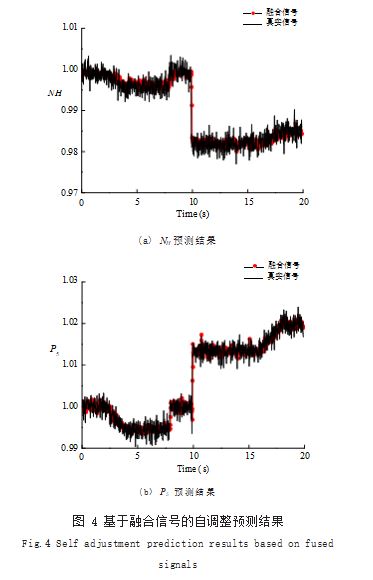
在图 3的多重控制系统时,在第 10s 注入压气机效率发生中等故 障, 即压气机效率 SE2-3%。Meta-OSELM 网络利用无故障的飞行数据进行离线训练,始终利用融合信号进行自调整预测,每次仿真模拟 20s,对各信号进行 50次仿真,结果如图 4 所示。
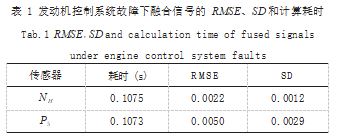
从图 4 中可以看出,在地面标况下,在 2s ~ 8s 和 10s ~ 18s 注入了燃油泵故障,因此各传感器均发生相 应的偏移,由于在第 10s 注入了气路故障,各传感器信 号均发生了突变。虽然在图 4(b) 结果中第 10s 的预测 结果有一定的偏差,并且由于本节设定的p 为 5.因此 整体的预测有滞后。但从信号的自调整预测结果可知, 各传感器的预测结果均能较好地跟踪真实信号。如表 1 所示显示了 50 次仿真具体 RMSE、SD 和计算耗时。
由表 1 结果可知,自调整预测模型计算传感器的 20s 仿真需要花费不到 0.11s。其中,P5 传感器对应的误差最大为 0.0050.保证提供精确的解析余度信号。各 传感器对应的 SD 也均低于 0.0029.预测结果均有一定 的稳定性。因此可以采用提出的基于决策级融合的自调 整预测模型提供解析余度。
2.2 发动机及控制系统故障诊断
由于自适应模型会根据传感器的偏差调整模型输 出,实现自适应模型与发动机输出相匹配的目的 [6]。因 此准确的故障定位信息对信号重构至关重要,若定位信 息错误,那么将会使用已故障的传感器信号进行状态监 测,这样将会导致模型阶段失效。考虑到故障诊断中出 现漂移故障以及微小偏置故障存在误诊的情况,采用定 位信息结合滑动窗口进行信号选择,如式(5)所示 :
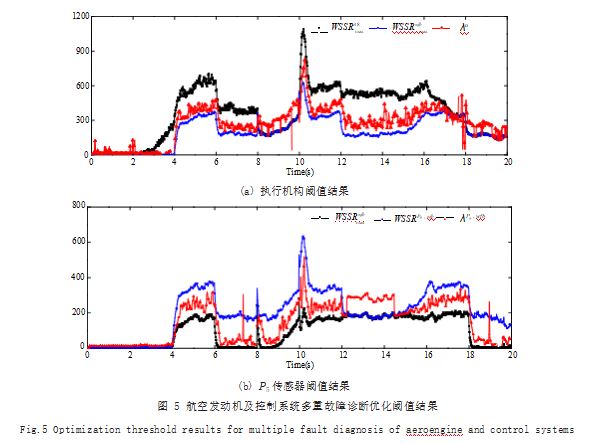
其中, n1k(c)为接收的 n1 传感器的故障状态,若诊断 出 n1 传感器发生故障,那么n1k(c)=1 ;否则, n1k(c)=0.结 合图 2 中的信号选择模块, 若式 (5) 成立, 那么选择预 测信号进行计算,否则选择传感器量测信号进行信号预 测。结合滑动窗口以及自调整预测模型的多重控制系统 故障诊断结果如图 5 所示。
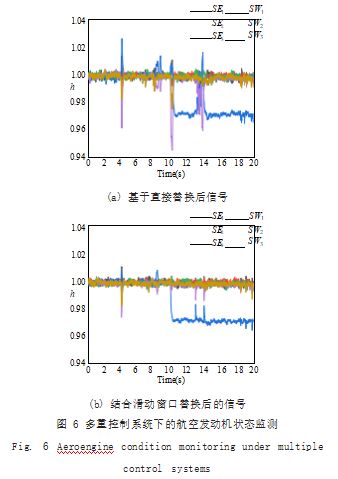
为了研究不同选择方式对重构信号的精度影响,重 构信息建立后,量测信号y 结合重构信息后产生的yK 与发动机模型的输出的偏差输入至 EKF 中,实现发动机的状态监测。为了进一步体现本节提出的航空发动 机及控制系统多重故障隔离方法的优越性,进行多重控 制系统故障下的航空发动机状态监测。如图 6 所示分别 展示了基于直接选择后信号以及结合滑动窗口替换后的 信号的状态监测结果。
从图 6 可知,无论是基于直接替换后信号,还是定 位信息结合滑动窗口替换后信号,压气机效率 SE2 均 能在第 19s 发生 -3% 的突变,并未被故障信号所影响。 图 6(a) 中基于直接替换的信号,在第 10s 和第 14s 的 诊断过程中, 分别出现 SE2 突变和 SE2 与 SE3 耦合现 象,这是由于直接替换信号在这些阶段错误的选择了故 障信号导致的,体现了控制系统多重故障诊断的重要 性。图 6(b) 中定位信息结合滑动窗口后,仅在第 4s、 13s、14s 和 20s 出现由传感器突变故障导致的较小单 次凸起,并很快将其消除,偏离的 SE2 与其他健康参数 完全分离,状态监测结果明显优于图 6(a) 的结果,较 好地实现了发动机的状态监测。
3 结语
本文针对发动机及控制系统故障问题,设计一种基 于决策级融合的发动机传感器自调整预测模型,可根据 传感器故障诊断结果调整解析余度输出。仿真结果表明, 自调整预测模型能够准确输出多个故障传感器的余度信号,此外,结合优化阈值与自调整解析余度信息,可提 升航空发动机及控制系统的多重故障诊断与隔离能力。
参考文献
[1] WILLERSRUD A,BLANKE M,IMSLAND L,et al.Fault Diagnosis of Downhole Drilling incidents Using Adaptive Observers and Statistical Change Detection[J]. Journal of Process Control, 2015.30:90-103.
[2] JIN P,LU F,HUANG J,et al.Life Cycle Gas Path Performance Monitoring with Control Loop Parameters Uncertainty for Aeroengine[J].Aerospace Science and Technology,2021.115:1-14.
[3] CHOW E,WILLSKY A.Analytical Redundancy and the Design of Robust Failure Detection Systems[J].IEEE Transactions on Automatic Control,1984.29(7):603-614.
[4] Zou W D,Yao F X,Zhang B H,et al.Improved Meta-ELM with error Feedback Incremental ELM as Hidden Nodes[J]. Neural Computing and Applications,2018.30:3363-3370.
[5] 李业波,蒋平国,田迪,等.航空发动机传感器解析余度模型的 建立方法[J].航空发动机,2018.44(4):67-71.
[6] 周浩文.基于核自适应滤波的航空发动机性能预测与故障诊 断研究[D].南京:南京航空航天大学,2020.
关注SCI论文创作发表,寻求SCI论文修改润色、SCI论文代发表等服务支撑,请锁定SCI论文网!
文章出自SCI论文网转载请注明出处:https://www.lunwensci.com/jisuanjilunwen/63582.html