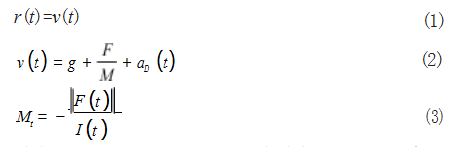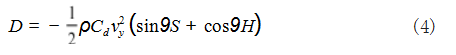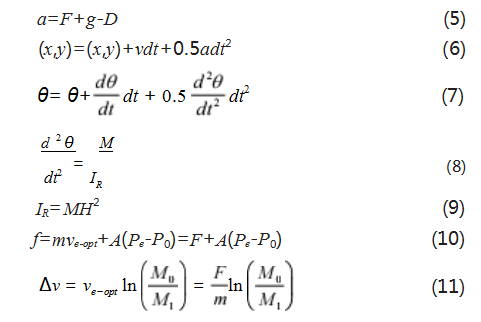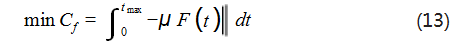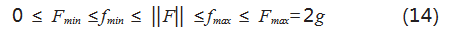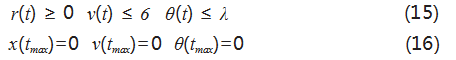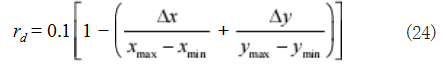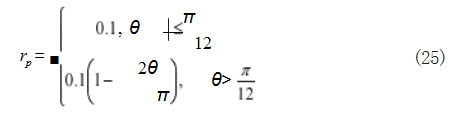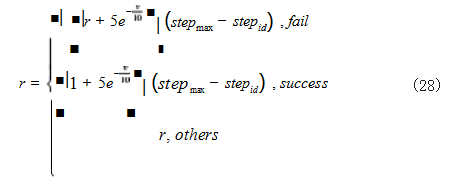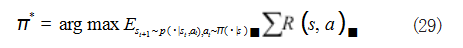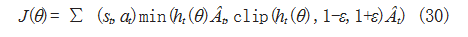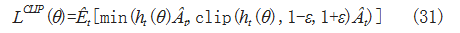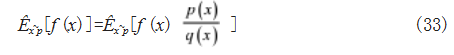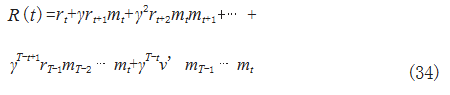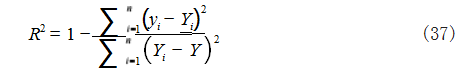SCI论文(www.lunwensci.com):
摘 要:运载火箭的制导回收实现对于航天发展具有重大意义, 在火箭回收任务中对回收精确制导、实时低时延的计算 能力有高标准,传统回收方法在解决该问题上表现出了一定的缺陷和局限性。本文对控制过程进行马尔可夫决策建模,通过构 造 PPO2 算法框架对整个回收过程进行实时求解,采用复合型奖励函数对位置、姿态、着陆阈值和燃料消耗进行相应约束,并 对其进行训练。实验表明,基于 PPO2 算法的回收制导模型可以较好地满足各项约束条件,并实现推力切换最优策略,证明了 PPO2 算法在处理该问题时可兼顾实时性和控制效果的优化性,对不同初始参数火箭型号和带有扰动的环境偏差均表现出较强 的适应能力,具有一定的泛化能力。
关键词:深度强化学习 ;PPO2 算法 ;决策制导
Sequential Decision Guidance Algorithm for Space Controller Based on PPO2
【Abstract】: The realization of guided recovery of carrier rocket is of great significance to aerospace development. In rocket recovery mission, high standards are set for precision guidance recovery and real-time low delay computing power. The traditional recovery method has some defects and limitations in solving this problem. In this paper, the Markov decision modeling of the control process is carried out. The PPO2 algorithm framework is constructed to solve the whole recovery process in real time. The compound reward function is used to constrain the position, attitude, landing threshold and fuel consumption, and the training is carried out. The experiment shows that the recovery guidance model based on PPO2 algorithm can better meet the constraints and achieve the optimal strategy of thrust switching, which proves that PPO2 algorithm can take into account the real-time and control effect optimization. It can realize strong adaptability to different initial parameter rocket models and environmental deviation with disturbance, and has a certain generalization ability.
【Key words】: deep reinforcement learning;PPO2 algorithm;decision guidance
0 引言
随着中国航天事业迅速发展, 空间站建设、地外行星探索以及轨道卫星部署任务加快推进,我国运载火箭发射进入繁密时期,而运载火箭作为空天往返任务的主 要运载器,在高频发射过程中的合理调度与重复发射显 得格外重要,运载火箭的成功回收和再次发射,对减少 发射成本和地外行星起降任务推进具有重要意义。我国 在火箭回收技术中,以群伞和缓冲气囊协同作用回收火 箭 [1],对火箭回收控制具有一定的效果,但可操作性不强。而现阶段,工程上一般采用气动力模型和动力学模 型,并通过不断调节矫正相关参数,使得能够完成运载 火箭的姿态调整,进而实现运载火箭的控制。但是该方 法兼容性较差、设计周期长、设计难度高,尽管具有较 高的可操作性,但却难以满足短期多型的实际需求。此 外, SpaceX 公司 [2] 应对火箭垂直回收采用凸优化方法, 面对制导问题,通过对多种问题进行优化以应对复杂的飞行环境,应用凸优化方法对于垂直返回的轨迹进行实 时规划、控制,成功在海陆均实现了火箭垂直回收。
而人工智能技术在解决类似的序列决策问题上获得了 较好的表现,随着人工智能技术在各领域的广泛应用,其 中以深度强化学习技术 (Deep Reinforcement Learing, DRL) 为基础的 DeepBlue 和 AlphaGo 展现出惊人水平, 也展现了深度强化学习算法在求解环境交互的决策问题 上具有较大优势。强化学习能够模拟实际情况与环境进 行不断交互,从而累计奖励求解最优策略。运载火箭的 回收控制实际上也是一个火箭在回收过程中的决策行为,因此本文应用深度强化学习对运载火箭回收问题进 行研究和模拟。本文的主要贡献如下:
(1)在传统回收方法中,实时优化 [3] 方法在实时 求解过程边值问题中的效果难以保证 ;而在凸优化方法 中,将参数优化问题构造为便于求解的二阶锥凸优化问 题这一过程的可操作性不强 ;以动力学模型为核心的回 收方法需优先得知环境约束和动力学建模,在回收情况 不确定时回收,难以具备兼容性。
(2)本文使用一个统一的深度强化学习框架对整个 回收过程进行实时求解,缓解了回收过程决策的割裂性 ; 利用 PPO2 算法使智能体与环境之间不断交互迭代,进 而得到回收过程的最优策略,仅需调整参数重新训练即 可获得新的策略,操作性较强 ;在非常规地区着陆或地 外行星探索等位置,以及在无法迅速构建环境模型的情 况下,具有环境自适应能力和泛化能力的本文模型,能 较好适应火箭、环境模型调整。
(3)本文利用深度强化学习有效实现了运载火箭回 收这一序列决策问题的实时全过程求解,在参数、模型 调整上也具有较高的可操作空间,能够完成在复杂、陌 生环境下的适应性回收着陆,与传统算法进行比较,验 证了本文方法的较强泛化能力。
1 相关工作
DRL 是融合了具有感知和决策能力的深度学习和 强化学习,而其在机器控制、机器视觉、工业制造、参 数优化等领域得到广泛应用 [4]。其中在机器控制领域, Levine 等人 [5] 利用深度学习模型,在机器手眼协调中 获得了较好效果, Lenz 等人 [6] 实现了动作控制的在线、 实时模型控制方法,在此基础上, Yahya 等人 [7] 实现多 模型的异步行为优化,再通过集中监督学习优化局部策略, 极大降低训练时间。在参数优化中, Hansen 等人 [8] 在 超参数优化控制上提出应用 Q 梯度下降方法,自动学 习不同任务的学习率。
而在运载火箭回收这一应用领域由于着陆过程中存 在大量不确定性,任务寻求者和设计人员一直在追求生 成可行或最佳在线轨迹的能力 [9]。当飞行任务须满足更严苛的要求时,通常需要解决具有路径约束及终端的轨 迹规划问题,例如载人任务。多项式制导起于 Apollo 计划,仍被用于火星着陆器。由于上述问题通常是非线 性的,因此很难解决,在过去的十年里只能离线求解。 为了简化这一系列问题,将 Apollo 登月舱的加速度设 计为关于时间的二次多项式。为了进一步提高航空航天 器制导的自主性,近些年计算制导这个新的研究方向得 到越来越多的关注 [10,11]。计算制导强调通过迭代优化计 算逐步取代传统的解析制导律, 并依靠鲁棒高效的计算方 法和先进的硬件计算平台, 来处理航空领域中针对非线性 动态系统的计算难题,突破传统方法的束缚 [10]。在计算 制导研究中,基于凸优化的在线轨迹优化是一个研究热 点,并得到了快速发展。美国实验室 JPL 的 Aç1kmeşe 和 Blackmore[12-14] 在对火星的着陆与控制领域做出了 巨大贡献,成功将之前未可靠求解的难题转换成凸优化 问题进行求解。
而现今,提升着陆轨迹优化的可靠性与计算制导效 率仍是学术界的研究难点,具有十分重要的学术价值和 潜在的应用价值。
2 问题描述
在运载火箭回收过程中,依据动力学原理建立如 式 (1)- 式 (3) 所示的运载火箭回收的动力学模型,由于 火箭在进行回收制动时,与水平地面的距离较近,由此可将地面视为平面,规定重力加速度g 在同一地理位置为常 量,并在惯性系下描述运载火箭回收过程中的质心运动。
其中 v(t) 和 Mt 分别表示运载火箭在 t 时刻的速度矢 量以及质量, I 表示火箭发动机比冲, aD (t) 表示空气阻 力加速度, r(t) 表示以目标着陆点为原点的火箭位置矢 量, F(t) 表示火箭的实时推力。
假定火箭回收环境中空气密度分布是均匀的,在运 载火箭着陆过程中,不同的倾角条件下火箭的竖直迎风 面积会发生变化,因此回收过程中的空气阻力表示为如 式(4)所示 :
ρ 表示为在当前高度的空气密度大小, S 为火箭横 截面积, H 表示火箭高度, Cd 为阻力系数。
根据以上动力学模型,可建立运载火箭在回收过程 中的运动模型,如式 (5)- 式 (11) 所示,用以具体描述火箭的运动指标数据变化:
其中 a 表示运载火箭实际加速度大小, g 为重力加 速度, f 表示实际推力, F 表示额定推力, (x,y) 表示火 箭的坐标, dθ/dt 表示火箭箭体角加速度, M 表示火箭 质量, IR 表示转动惯量, m 表示燃料质量流量, Pe 为发 动机喷嘴处的压强, P0 为外界环境压强, ve-opt 为火箭的 排气速度, A 为比例系数, M0、M1 表示火箭在不同时间的质量。
在运载火箭回收着陆过程中,需要遵循以下四种约束。
2.1 燃料分配
火箭燃料主要由煤油、液氢、液氧、片二甲肼等混 合构成,火箭的燃料成本昂贵,而运载火箭的燃料贮箱 空间有限,在航天火箭的垂直回收过程中,需要综合考 虑火箭每一时刻不同的工作状态,结合燃料的体积、类 型来进行正确合理的分配安排,以达到最优的火箭回 收。而火箭燃料消耗与发动机推力值呈正相关,表示为 如式 (12) 所示:
在运载火箭回收任务中,将连续动作的发动机推力 值按比例进行求和,得到燃料消耗优化的目标函数,如式 (13) 所示:
其中 Cf 表示燃料消耗量, μ 为比例系数。
2.2 发动机推力约束
航天运载火箭在各个飞行航段所需要的动力不同, 对火箭所需推力进行正确的模拟优化,对运载火箭回收 策略有效性和准确性具有重要意义,本文中设定火箭推 力约束如式(14)所示:
其中 Fmax 和 Fmin 为额定最大、最小推力, fmax 和fmin 为实际最大、最小推力。
2.3 着陆末状态约束
航天火箭在垂直回收的过程中,需要结合外界气 压、水平风阻以及火箭自身的质心偏移来对回收部分的 姿态落点进行调节,即找寻最优轨迹与最佳落点。为保 证运载火箭成功回收,综合考虑过程约束与终端约束, 选取如式 (15) 所示的约束形式 [15] ,结合深度强化学习 与火箭回收系统,将式 (16) 作为终端条件,以求找到 最小偏差点、最优轨迹曲线。
其中 6 和 λ 为着陆末状态的速度、箭体角度阈值。
2.4 陆支架设计
运载火箭的回收过程中,陆支架同样不可或缺。作 为垂直起降可重复使用运载器的关键部件之一,陆支架 的性能会直接决定运载器能否安全着陆和重复使用。陆 支架的设计主要涉及两个方面,分别是参数指标和功能 要求,前者主要是为了限制陆支架的结构和规模大小, 防止陆支架尺寸不合导致的不能很好地装配在运载火箭 上;后者的作用是使设计的陆支架能够满足使用火箭垂直回收的需求,避免出现回收着陆失败的可能。按照 贾山等人所设计的运载火箭着陆装置进行模型构建 [16], 对陆支架进行以下设计约束 [17] 要求,如式(17)所示 :
其中 S 为运载火箭缓冲装置的竖直方向距离, ∆ 为 火箭回收部分着陆结构最低点距地面的保障安全间隙, T 为陆支架底部高度。
3 MDP 设计与 DRL 算法
本文对运载火箭的回收过程进行建模,采用 DRL 方法求解最优策略和进行实验,整体架构如图 1 所示。
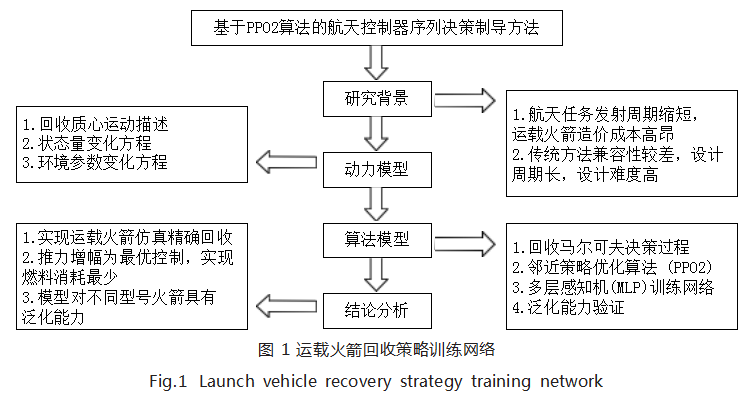
3.1 马尔可夫决策过程设计
深度强化学习过程通常可以抽象表示为一个马尔可 夫决策过程 (Markov Decision Process,MDP) 模型, 其中一个 MDP 模型由状态量、行为量、状态转移概率 和奖励函数组成,具体而言,一个马尔可夫决策过程可 以采用四元组形式表示,如式(18)所示 :
3.1.1 状态量 S
马尔可夫决策过程中 S 为状态量,本过程中使用水 平坐标、垂直坐标、水平速度、垂直速度、角速度、角 加速度、发动机角度以及运行时间等 8 种指标描述火箭在 回收过程中的状态,其中为简化空间条件、加快训练速度, 对操作空间的范围进行约束,具体表示为如式(19) 所示 :
3.1.2 行为量A
A 表示行为量,由推力加速度和发动机角速度两部 分组成,每时间步的推力加速度设定为介于 0.2g 和 2g 之间的稳定值,发动机角度可以 30° /s 的角速度进行调整,表示为如式(20)所示 :
由于具体行为表现为连续动作,需根据概率分布函 数得到行为的概率分布选择执行动作,而因为动作函数 表现为非连续型变量,难以准确选择密度分布函数,因 此在行为空间特征取样,对其进行离散化处理,将行为 量简化为推力加速度和发动机角速度等发动机离散控制信号组成的多维矢量集合,具体如式(21)所示 :
3.1.3 状态转移概率 P
结合状态量和行为量, 在某状态 st 下根据火箭回收模型和相应动作 at ,可计算得出转移的确定性状态 st+1, 即可得到相应状态转移函数,如式 (22) 所示 :
按照回收过程中的时间步周期 dt 对状态转移函数进行离散化,可得到状态转移概率,如式(23)所示 :
3.1.4 奖励函数 R
本问题中根据实际要求,对火箭着陆过程和回收是 否成功,需要做几点约束奖励条件。
在悬停任务中,箭模型需要遵守的奖励机制为 :
(1) 火箭与目标位置的距离 :距离越近,奖励越大 ;
(2) 火箭体的角度 :火箭体应尽可能保持竖直, 即 火箭体角度保持接近 0 ;
(3)燃料消耗 :火箭动作应尽可能执行燃料消耗小 的动作,以降低燃料能源消耗。
在着陆任务中,即火箭在着陆时也要遵循一种类似 的奖励机制 :
(1)着陆速度 :着陆速度小于安全阈值 ;
(2)着陆角度 :航天火箭角度接近数值 0 时,奖励 越大 ;
(3)距离偏差 :航天火箭着陆时与预定着陆点之间 的距离越小,奖励越大 ;
(4) 时间周期消耗 :火箭着陆过程末状态时, 消耗 的时间周期越少,奖励越大。
根据上述两点约束条件,仿真设计使用复合型奖励 函数,包括位置约束奖励、姿态约束奖励、燃料消耗奖 励和末状态约束奖励。在位置约束奖励函数 rd 中,通过 对火箭位置和目标位置的距离关系进行描述,使得火箭 位置越接近目标位置所获得的奖励越大,并且该形式奖 励函数在对火箭的回收运动方向训练引导上表现出较好的作用,具体表示为如式(24)所示 :
其中 ∆x、∆y 为当前位置与目标位置的坐标距离差, xmax、xmin 表示试验检测区域左右区域坐标, ymax、ymin 表 示试验检测区域上下区域坐标。
在姿态约束奖励函数 rp 中,主要侧重于对火箭体垂 直倾角情况进行评价,从而给出相应的奖励,表示为如 式(25)所示 :
在燃料消耗奖励函数 re 中,将燃料消耗作为惩罚项,用于引导火箭在每时间周期采取燃料消耗最优的动 作,而在实际过程中,燃料消耗通常与推力值大小呈现正相关,因此函数表示如式(26)所示 :
结合式 (24)、 式 (25)、 式 (26) 可得, 火箭 回收着 陆过程中的奖励函数如式(27)所示 :
对于末状态约束而言,针对于火箭回收着陆过程的末状态,对火箭是否成功回收两种情况,分别应用不同策 略计算奖励,并根据所消耗的时间周期数多少,对状态奖励进行放大,加快深度强化学习的进程,具体表示为如式(28)所示 :
其中 stepmax 表示一次回收过程的最大时间步, stepid 表示当前时间步。
在奖励函数中,分别对位置、姿态和燃料消耗进行约束,在末状态和中间状态采用不同策略生成奖励,使用深度强化学习对火箭回收着陆策略进行训练,从而得到最优策略。
3.2 DRL 算法选择
本文需要解决运载火箭回收这一序列决策问题的最 优策略,而在传统方法中,实时求解过程边值问题中的 效果难以保证,无法对全过程进行更优求解。而在强化 学习算法中,尽管采用了重要性采样,但缺陷在于采样 分布不能相差太大,会导致算法难以收敛,而且同一批 次数据仅能进行单次训练,极大限制了参数的更新速度 与训练进程。而 PPO2 算法实现了使用一个统一框架 实时求解火箭回收全过程最优策略,兼顾了求解该问 题的实时性和控制效果的优化性。除此之外, PPO2 算 法在离线环境下的限幅处理解决了重要性采样的缺陷, 能对收集到的数据进行重复使用,限制网络更新幅度, 实现小批次数据的多次训练,提高了参数的更新速度。 因此,本文选择使用邻近策略优化 (Proximal Policy Optimization ,PPO) 算 法,PPO2 算 法 为 PPO 算 法 的一类,基于 Actor-Critic 框架,算法中智能体与环境 不断进行交互,按照式 (29) 作为目标函数,以奖励期望最大为目标,求解火箭回收过程中的最优策略。
PPO2 算法中包含 Actor 策略网络和 Critic 评价网络, 其中策略网络输出行为量下对应的概率分布,并通过采 样获取执行动作,而评价网络则输出对输入状态的奖励。 PPO2 算法按照如式(30)所示进行网络参数更新 :
PPO2 算法引入超参数 ε ,使用截断函数来控制网络 参数 θ 的梯度更新,其中 Clip 为限幅函数,将重要性权 值限制在 1-Ε 和 1+Ε 之间,防止网络更新速度过慢或过 快而导致的难以收敛,使用 Pytorch 库中的 Clamp 函 数,截断函数表示如式(31)所示 :
其中 ht (θ) 为重要性权值,是通过重要性采样计算 得出,定义为网络不同状态下的概率分布比值,本文中使用网络不同状态为相邻态,表示如式 (32) 所示 :
由于网络不同状态具有不同的策略 πθ 和 πθ ',从而 获取不同的概率分布p 和 q,通过 πθ ' 策略收集数据, 得到一系列概率分布p 序列,而使用 πθ 策略进行计算 梯度反向传播。因此算法使用了重要性采样,对不同策 略之间进行修正处理,将无法从p 中采样的情况,转换为从 q 中采样,采样公式如式 (33) 所示 :
PPO2 算法的运载火箭回收的仿真模拟算法流程如下 :
步骤 1 :将 8 维初始状态量 s 作为输入量输入使用 πθ ' 策略的 Actor 网络,输出动作分布概率和动作抽样 结果,经过火箭回收运动模型计算得到下一状态 s', 并 将其输入使用 πθ ' 策略的 Critic 网络, 输出状态的 vs' 和 相应奖励 Reward,再将 s' 状态输入 Actor 网络,重复 过程直到一次回收过程结束,并记录过程状态序列 [s]、 动作序列 [a] 和概率序列 [p]。
步骤 2 :将步骤 1 中得到的末状态 sT 的 vs' 作为 v', 计算累计奖励期望,并引入衰减因子 γ,防止未来奖励对 结果影响较大,在本文中额外引入状态判断量 mt 对运载 火箭各状态回收是否完成进行判断, 奖励函数如式(34) 所示 :
对回收过程中各状态计算得到累计奖励列表 [R[0], R[1]⋯R[T]],其中 T 代表回收过程中的末状态计数。
步骤 3 :将步骤 1 所得状态 [s] 输入使用 πθ 策略的 Critic 网络, 输出 [vθ] 序列, 结合步骤 2 所得累计奖励 列表 [R],依据公式 (35) 计算得出优势函数 Ât ,用以表 示实际奖励和理论奖励的差距。
步骤 4 :计算 Critic 的损失函数,对步骤 3 所得优势取均方误差,并将损失进行反向传播更新 Critic 网络, 如式(36)所示 :
步骤 5 :将步骤 1 所得的状态序列 [s] 输入使用 πθ 策略的 Actor 网络,并按照动作序列 [a] 获取相应动作 概率pθ (at |st),按公式 (32) 计算重要性权值 Ratio。
步骤 6 :根据步骤 3 和步骤 5 得到的优势函数和重 要性权值,根据公式 (36) 计算 lossactor ,并对其进行反 向传播更新 Actor 网络。
步骤 7 :循环步骤 1 至步骤 6,直至训练结束或累 计奖励期望收敛。
4 训练与实验分析
根据前文构架的运载火箭回收模型及 PPO2 算法,本 文设计带有映射层的多层感知机 (Multi Layer Perceptron, MLP) 形式的神经网络,使用拟定的 MDP 对火箭回收 策略进行训练。
4.1 训练网络设计
回收策略训练网络由输入层、映射层、隐藏层和输 出层组成,在输入层中,按照火箭回收 MDP 中的 8 维 状态量作为输入,在经过映射层时,将连续输入的 8 维状态数据映射到 120 维高维空间,使得预测可以更加逼 近高维函数,中间包含多层含有 128 个节点的隐藏层, 隐藏层间使用 LeakyReLU 作为激活函数,最后输出层 输出动作分布概率和状态评价 vt 值, 网络优化算法选择 Adam 算法。以运载火箭回收过程中各状态累计奖励作 为评价标准,从而对火箭回收策略模型进行训练。
4.2 训练结果分析
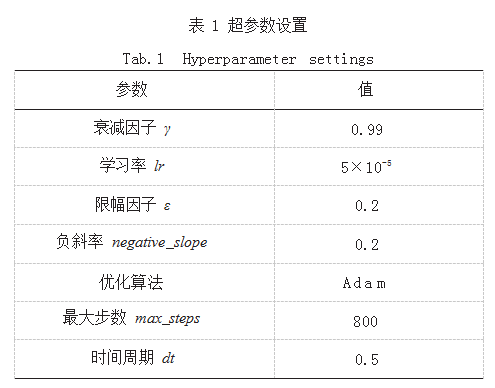
按照运载火箭回收过程中各状态的累计奖励作为评价标准,基于火箭回收过程 MDP 和训练网络,对火箭 回收策略进行训练。通过智能体与环境的交互,获取 k 组过程数据,计算该 k 组过程的平均累计奖励,若平均累计奖励相较前状态单调增加,则按照这 Epochs 组数据依次对策略网络 πθ 进行更新 ;若平均累计奖励不及之前,则依旧采用历史最优策略 πθ '。本文中使用 PPO2 算法和 A2C 算法两种算法分别对火箭回收策略模型进 行训练,网络的超参数设置如表 1 所示。
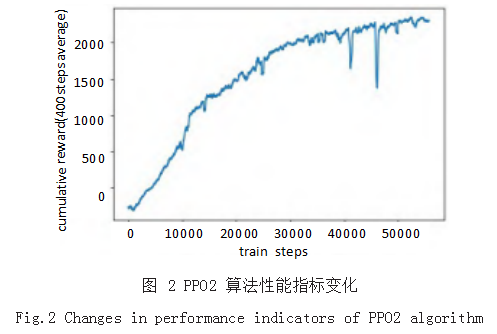
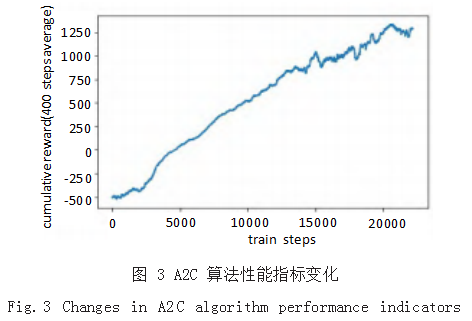
PPO2 算法和 A2C 算法两种算法分别在经过 56000 次和 23000 次训练后,累计奖励达到收敛,如图 2 和图 3 所示,累计奖励分别由 -457.07 提升到 2156.84, -507.39 提升到 1291.14,性能指标提升百分比绝对值 分 别 为 571.88% 和 354.47%, 其 中 PPO2 算 法 相 较 于 A2C 算法性能提升达 67.04% , 表明 PPO2 算法和 A2C 算法均可以实现对运载火箭回收策略的训练,但在 由累计奖励组成的性能指标表现上, PPO2 算法较 A2C 算法表现更佳。
在训练过程中, PPO2 算法和 A2C 算法均呈现上升 趋势,在训练达 10000 次时,两种算法累计奖励分别为417.53 和 452.23,A2C 算法较 PPO2 算法提升 8.31% ;在 训练达 2000 次时, 累计奖励分别为 1300.25 和 943.47, 此时 PPO2 算法较 A2C 算法提升 37.82%,由此可以认为,在训练初始阶段两种算法对运载火箭回收策略训练效果类似,但随着训练地进行, PPO2 算法的效果更优。
4.3 仿真模拟实验
4.3.1 实验目的及内容
为验证 PPO2 算法与 A2C 算法对同一类型运载火 箭在回收着陆过程中的性能好坏,根据对运载火箭回收 策略训练结果, 固定网络参数为 πPPO 和 πA2C, 按构建的 MDP 分别对同一状态的同型火箭进行仿真回收,按照 与策略训练过程中类似的初始条件,对运载火箭的状态 量 s 进行设置,以回收过程末状态 s' 是否满足回收的末 状态约束作为判断是否成功回收的条件,结果如图 4、 图 5 所示 :
4.3.2 实验结果
由图 4、图 5 可以看出两种算法均可以实现在仿真 环境下的运载火箭回收决策,末状态均满足着陆约束条 件,在回收过程中, PPO2 算法的速度变化时刻较为集 中, 表现为 250 至 300 时间周期中由 87.13m/s 减小至 18.71m/s, 而 A2C 算法的速度变化在全过程中较为均 匀 ;在箭体角度变化过程中,两种算法表现较为接近,均可将角度控制在较小范围内。
根据速度和角度的变化趋势可以看出两种算法在 推力加速度输出策略上具有明显差异,如图 6、图 7 所 示, PPO2 算法在回收过程的前期,保持最小推力输出 对运载火箭姿态进行调整,在回收后期使用较大推力 将火箭调整至满足着陆约束条件,该推力切换方式满 足 Bang-Bang 最优控制 ;而 A2C 算法在回收过程的 大多时刻均采用较大推力,在后期大部分时刻使用最大 推力。其中 PPO2 算法、A2C 算法在回收过程中的平 均推力加速度为 5.83 和 6.51,由于燃料消耗与运载火 箭推力值呈正相关,因此可以认为在回收过程中 A2C 算法较 PPO2 算法多消耗 36.93% 的燃料。由此可知, PPO2 算法不仅能较好地实现运载火箭回收,还可以将 回收过程的燃料消耗控制在较低水平。
4.4 泛化能力验证实验
4.4.1 实验目的及内容
为验证运载火箭回收模型的泛化能力,本文采用型 号不同于训练火箭 α 型的火箭 β 型,两种火箭在各运载 火箭物理参数上均具有差异,且具有不同数值的动作方 式,由于气动阻力等部分环境因素受火箭物理参数的影 响,因此不再引入环境参数扰动,再次进行仿真实验。
4.4.2 实验结果
两种型号的火箭回收过程结果如图 8、图 9 所示, 此两种类型的火箭在回收过程中的数据变化大致相同, 根据公式 (37) 计算火箭 β 型对于火箭 α 型的拟合优度R2 :
经计算得,两种型号火箭在回收过程的速度变化 中拟合优度为 0.9970, 在运载火箭箭体角度变化中为 0.9974, 表现出不同型号火箭在回收过程中的数据变化 拟合度较高,并且推力增幅均满足 Bang-Bang 最优控 制,由此可见基于 PPO2 算法的火箭回收策略模型具有 对不同参数输入的泛化能力。
5 结论
本文研究了运载火箭的回收方案,构建了运载火 箭回收模型及其 MDP,设计带有映射层的 MLP 网络, 分别利用 PPO2 算法和 A2C 算法对回收模型进行训练, PPO2 算法的性能指标最终达到 2156.84,较 A2C 算法 提升到 67.04%,能够满足着陆阈值条件约束实现较为 精确的回收,并在推力增幅控制上满足最优控制条件, 实现较少的燃料消耗。该模型在应对不同型参数输入 时,能取得较好的回收效果,得到与训练型号相比较高的拟合优度,具备对不同参数输入的泛化能力。本文提 出的基于 PPO2 算法的运载火箭回收方案可实现在运载 火箭边缘端的火箭自主控制回收或远程控制,具有一定 程度上的现实价值和工程价值。目前,现有航天发动机 推力值大,但存在调节能力较弱的问题,未来在推力切 换及交接班条件上还有待进一步探索,除此以外,加大 算法更新迭代力度和计算硬件化也是推进工程实践的重要手段。
参考文献
[1] 高朝辉,张普卓,刘宇,等.垂直返回重复使用运载火箭技术分 析[J].宇航学报,2016,37(2):145-152.
[2] 宋雨,张伟,苗新元,等.可回收火箭动力着陆段在线制导算法 [J].清华大学学报(自然科学版),2021,61(3):230-239.
[3] LU P.Propellant-optimal Powered Descent Guidance[J]. Jour-nal of Guidance,Control,and Dynamics, 2018,41(4):813-826.
[4] 刘全,翟建伟,章宗长,等.深度强化学习综述[J].计算机学报, 2018,41(1):1-27.
[5] LEVINE S,PASTOR P,KRIZHEVSKY A,et al.Learning Hand-Eye Coordination for Robotic Grasping with Deep Learning and Large-Scale Data Collection[J]. International Journal of Robotics Research,2016,37(4-5): 421-436.
[6] LENZ I,KNEPPER R,SAXENA A.Deepmpc:Learning Deeplatent Features for Model Predictive Control[C]// Proceedings ofthe Robotics Science and Systems.Rome, Italy,2015:201-209.
[7] YAHYA A,LI A,KALAKRISHNAN M,et al. Collective Robotreinforcement Learning with Distributed asynchronous Guidedpolicy Search[C]//IEEE International Conference on Robotics and Automation,2016.
[8] HANSEN S.Using Deep Q-learning to Control Optimiz ationhyperparameters[J].2016
[9] YU Z S,CUI P Y,CRASSIDISJ L.Design and Optimization of Navigation and Guidance Techniques for Mars Pinpointlanding:Review and Prospect[J].Progress in Aerospace Sciences,2017,94:82-94.
[10] LU P.Introducing Computational Guidance and Control[J].Journal of Guidance,Control,and Dynamics, 2017,40(2):193.
[11] TSIOTRAS P,MESBAHI M.Toward an Algorithmic Control Theory[J].Journal of Guidance,Control,andDynamics,2017,40(2):194-196.
[12] AÇI KMEŞE B,PLOEN S R.Convex Programming Approach to Powered Descent Guidance for Mars Landing[J].Journal of Guidance,Control,and Dynamics, 2007,30(5):1353-1366.
[13] BLACKMORE L,AÇIKMEŞE B,SCHARF D P.Minimum- landing-error Powered-descent Guidance for Mars lan- ding Using Convex Optimization[J].Journal of Gui-dance, Control,and Dynamics,2010,33(4):1161-1171.
[14] AÇIKMEŞE B,CARSON J M,BLACKMORE L.Lossless Convexification of Nonconvex Control Bound andPointing Constraints of the Soft Landing Optimal Control Pro- blem[J].IEEE Transactions on Control Systems Technology, 2013,21(6):2104-2113.
[15] 程光辉.火箭垂直回收轨迹优化与制导技术研究[D].哈尔 滨:哈尔滨工业大学,2020.
[16] 贾山,赵建华,陈金宝,等.可复用运载火箭着陆装置展开与 着陆分析[J].航天返回与遥感,2022,43(5):11-23.
[17] 肖杰.重复使用运载器着陆支架展开锁定机构设计与性能 分析[D].南京:南京航空航天大学,2017.
关注SCI论文创作发表,寻求SCI论文修改润色、SCI论文代发表等服务支撑,请锁定SCI论文网!
文章出自SCI论文网转载请注明出处:https://www.lunwensci.com/jisuanjilunwen/63437.html