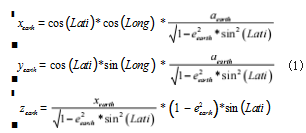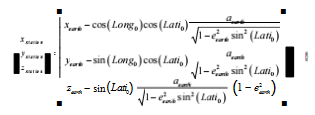SCI论文(www.lunwensci.com)
摘 要:针对有源探测定位方法存在的隐蔽性差的问题,本文设计了基于多源电子数据的目标测向定位算法。该算法基于 二维平面直角坐标系,首先进行经纬度转换,再以求出的定位点到各个测向线的距离作为判断基准,采用最小二乘法求解,然 后利用求出的定位点到各个测向线的距离对 x 轴和y 轴上定位点方差进行估计,最后基于方差得到误差椭圆的长轴、短轴和偏 角数据。实验结果表明,在平台点数量和位置发生动态变化的情况下,该方法仍然可以基于测向数据准确地对目标进行定位, 具有一定的鲁棒性。
Target Location Algorithm Based on Multi-source Electronic Data
ZHAO Jingzhe1. TIAN Han1. ZHAO Liqing2. WANG Yuan2.3
(1 .The 27th Research Institute of China Electronics Technology Group Corporation, Zhengzhou Henan 450047;
2.State Key Laboratory of Networking and Switching Technology, Beijing University of Posts and Telecommunications,
Beijing 100876;3.School of Systems Science, Beijing Normal University, Beijing 100875)
【Abstract】:Aiming at the problem of poor concealment of active detection and location methods, a bearing- only target location algorithm based on multi-source electronic data is designed in this paper. The algorithm is based on the two-dimensional plane rectangular coordinate system. Firstly, the longitude and latitude are transformed, and the distance from the positioning point to each direction-finding line is used as the judgment benchmark, which is solved by the least square method. Then, the variance of the positioning point on the x-axis and y-axis is estimated by using the distance from the positioning point to each direction-finding line. Finally, the major axis, minor axis and deflection angle of the error ellipse are obtained based on the variance. The experimental results show that when the number and position of platform points change dynamically, the proposed method can still locate the target accurately based on direction-finding data, and has certain robustness.
【Key words】:multi-source;target location;error ellipse;electronic data
0 引言
传统的有源探测定位方法需要定位平台向外发射电 磁波,因此容易受到外界干扰、隐蔽性较差。而无源探 测定位方法接收目标的辐射,通过提取电磁波中所含的 信息而获取目标的位置信息,不需要定位平台向外发射 电磁波,具有隐蔽性好、作用距离远等优点。
测向定位是无源探测定位中最常用的定位技术。测向定位技术适用于多种传感设备对目标进行定位,例如 红外成像设备、声呐、星载相位干涉仪等 [1-3]。现阶段 存在一些对测向定位技术的研究,例如,单站测向定位 算法对不定时辐射目标具有强的适用性 [3]。针对无源双 站测向交叉定位算法的精度进行分析,并对测向站位 置的部署给出了合理化建议 [4]。为了解决传统测向交叉 定位产生虚假定位点的问题,一种多点联合测向定位算法,可以对多个干扰源进行准确定位 [5]。文献 [6.7] 则 提出了一种新的基于改进 K-means 的聚类融合定位算 法,结果证明该方法在进行多站交叉定位时具有更好的 定位效果和鲁棒性。
本文基于现有的理论成果,设计了基于多源电子数 据的目标测向定位算法,该算法可以通过无源测向数据 实现对空中静态目标的定位和误差椭圆估计,并且支持 平台点数量和位置的动态变化。
1 目标定位算法
1.1 算法流程
基于测向数据,通过坐标转换和最小二乘法实现对 目标的定位,并且当平台点数量和位置发生动态变化 时,本文提出的算法仍然可以对目标进行准确定位,具 有一定的鲁棒性。该算法基于二维平面直角坐标系,首 先进行经纬度转换,再以求出的定位点到各个测向线的 距离作为判断基准,进行最小二乘法的求解,然后利用 求出的定位点到各个测向线的距离进行对 x 轴和y 轴上 定位点方差的估计,最后利用得到的方差,同时根据误 差椭圆的定义得到误差椭圆的长轴、短轴和偏角数据。
1.2 经纬度转换
由于经纬度是地球上的球体坐标,这里需要将其转换成平面直角坐标系。首先要得知地球的 3 个参数 :aearth 地球赤道半径, bearth 地球极半径, eearth 地球第一偏心率。
在进行坐标转换时将所有点向海拔高度为 0 的位置进 行投影,这样能够减少一个维度。首先将经纬度 Long、 Lati 转换成地心直角坐标系下的坐标 xearth , yearth , zearth, 如式(1)所示 :
这就构造了一个立体直角坐标系,以地心为原点, 实际 应用效果并不好,所以选择一个距离我们数据较近的点作为 原点,建立站心直角坐标系xstation , ystation , zstation ,选择点 的经纬度和高度为Long0. Lati0. Height0.如式(2)所示 :
而 x=xstation,y=ystation ,即算法需要的 x 和y。
1.3 求定位点
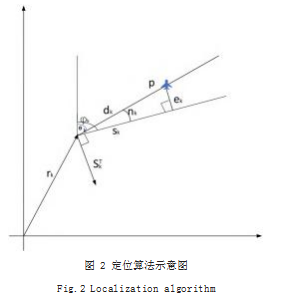
在单站多个时间测向交叉定位中,由于各个时间的 观测都存在一定的误差,因此,将会产生多个交点,如 图 1 所示。定位算法的目标是在这些交点区域内找到一 个最好评估位置p。首先建立直角坐标系,如图 2 所示。
其中 rk 为一个向量,代表从源点指向测向数据点的 向量, pk 代表向度,则 sk 为一条射线,是测向数据标识 的测向线。而p 点代表估计的定位点,则认为实际的示 向度应该是 θk ,此时的测量误差为 nk , dk 为测量点到定 位点的距离。从点p 做 sk 的垂线, 得到向量 ek , 而 sk(⊥)为 sk 的正交向量。
定义 ηk,其中 k=1 到 N, ηk=|ek | 表示p 到第 k 个观察 点检测到的 DF(Direction Finding) 的距离, 因此我 们可以利用最小二乘法来解决这个问题 :找到一个估算 位置p,使得p 到每一个 DF 的距离之和{ 插图 }最小。对点p 的位置,可以看做如式(3)所示 :
式 (3) 两边同时乘 sk(⊥),得到如式(4)所示 :
并采用最小二乘法求解。
最后得到结果p^ 即定位点。得到定位点后,如果 存在高度这一维度, 且知道俯仰角 β 的情况下, 可以得 到每个测向数据估计的高度,如式(7)所示 :
1.4 求误差椭圆
求误差椭圆的基本方法是根据目标位置在 X 轴方向 和 Y 轴方向的标准偏差来计算误差椭圆的旋转角度,短 轴和长轴。误差椭圆的长轴方向表示目标的位置具有最 大的不确定性,也就是精度最差方向 ;误差椭圆的短轴 方向表示目标的位置具有最小的不确定性,即精度最好 方向。而通过测向数据得到的定位点同样因为误差具有 偏差,因此可以利用这个特点求得定位点的误差椭圆。
ηk (其中 k=1 到 N)表示 P 到第 K 个的观察点检测 到的 DF 的距离。
RMS (Root Mean Square) 为观察站的测量结果的标 准差,由于本系统的观察站是基于 Radio-goniometry 系统, 根据 CS 公司的测试数据,Radio-goniometry 系 统的 RMS 为 0.5 度。 dk(^) (其中 k=1 到 N)表示根据定位 算法计算出来的目标源位置的估计值到观察站的距离。
pe 表示误差椭圆的概率特征。当pe=99% 的时候, 表示被检测的目标有 99% 的可能性落在误差椭圆里面,默认的时候系统采用的pe 值可以为 99%。
向量e = (∇x, ∇y )为目标位置误差的一个行向量。 再定义误差协方差矩阵 Q^,如式(8)所示 :
P 表示位置不确定性的误差协方差的实对称矩阵,如式(9)所示 :
e 服从正态分布,其密度函数如式(10)所示 :
误差椭圆的旋转角度计算过程如下 :
其中, λ1 是矩阵 P 的最高本征值 ,λ2 是矩阵 P 的最 低本征值。
则误差椭圆的计算公式如表 1 所示。根据表 1 我们 可以知道在一定的观察站情况下,主要有 3 个因数对定 位的精确度产生比较大得影响, (1)是观察站测量得到 的方位角的误差 nk ;(2) 是辐射源目标和观察站之间的相对距离 ;(3)是观察站和辐射源目标的相对角度。
2 仿真结果
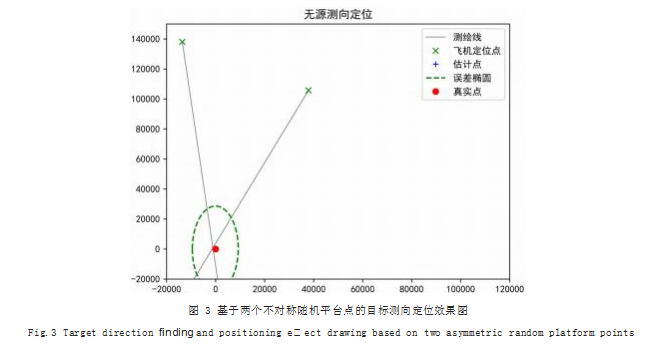
(1)基于两个不对称、随机平台点对目标进行测向 定位,平台点、目标点和估计点的详细信息如表 2 所 示,定位效果如图 3 所示。
通过表 2 和图 3 可知,在基于两个不对称随机平台 点进行目标测向定位时,估计点同样接近于目标点,定 位效果较好。经计算,其误差椭圆的长轴为 4478.12. 短轴为 994.461.偏角为 2.96.
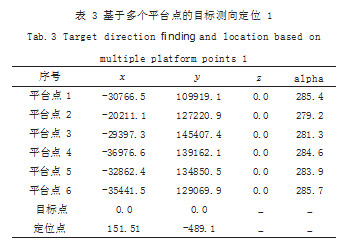
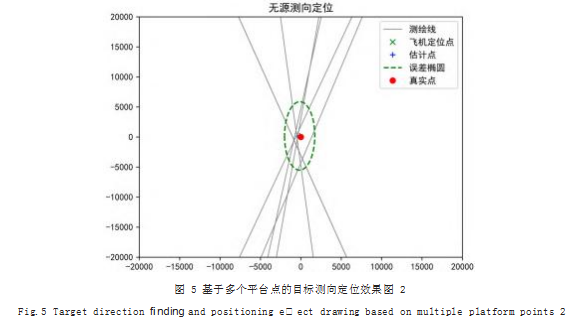
(2)基于多个平台点对目标进行测向定位,平台 点、目标点和估计点的详细信息如表 3、表 4 所示,定 位效果如图 4、图 5 所示。
通过表 3、表 4 和图 4、图 5 可知,在基于多个平台点进行目标测向定位时,同样可以获得较好的定位效 果。经计算,图 4 中的误差椭圆的长轴为 14644.3.短 轴为 619.489. 偏角为 3.37611 ;图 5 中的误差椭圆的 长轴为 2611.75.短轴 623.309.偏角为 3.09326.
综上所述,当平台点数量、相对位置以及绝对位置发生动态变化时,提出的算法仍然可以对目标进行较为 准确的定位,具有一定的鲁棒性。
3 总结与展望
本文借助于无源测向定位的理论成果设计了基于多 源电子数据的目标测向定位算法,算法通过经纬度转 换、最小二乘法等实现了对空中静态目标的定位和误差 椭圆估计。最后通过实验证明,提出的方法可以基于测 向数据较为准确地对目标进行定位,并且支持平台点数 量和位置的动态变化,具有一定的鲁棒性。未来还需要 对目标的连续定位问题展开研究。
参考文献
[1] 岳娟,高思莉,李范鸣,等.基于GPS的红外成像测向交叉定位方法[J].激光与红外,2019.49(12):1447-1454.
[2] 俞剑,王益乐.被动声呐多阵测向交叉定位的数据关联算法 [J].指挥信息系统与技术,2018.9(3):65-69.
[3] 冯永会,葛俊祥,李浩.无线测向定位算法及实现系统[J].电子 测量与仪器学报,2017.31(10):1602-1607.
[4] 谢鑫.测向交叉定位最优布站方案分析[J].电子科技,2014. 27(8):85-89.
[5] 陈圣哉,彭章友.基于无人机的多干扰源多点联合测向定位 算法研究[J].电子测量技术,2020.43(12):85-90.
[6] 张靖,段富.优化初始聚类中心的改进K-means算法[J].计算 机工程与设计,2013.34(5):1691-1694+1699.
[7] 孙鹏,熊伟.测向交叉定位系统中的K-means聚类融合算法 [J].电光与控制,2016.23(10):36-40.
关注SCI论文创作发表,寻求SCI论文修改润色、SCI论文代发表等服务支撑,请锁定SCI论文网!
文章出自SCI论文网转载请注明出处:https://www.lunwensci.com/jisuanjilunwen/62613.html