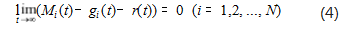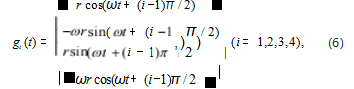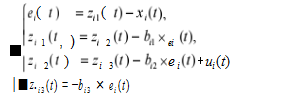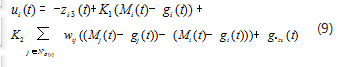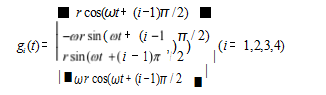SCI论文(www.lunwensci.com)
摘 要 :多智能体协同编队问题是多智能体研究的热点问题。本文主要研究了扰动环境下四旋翼无人机群的编队控制问 题。首先对不含扰动的时变编队控制算法进行学习仿真;然后由于扰动因素风的存在,提出自抗扰控制技术来抑制扰动;最后 将时变编队控制算法和自抗扰控制技术相结合,实现对扰动环境下无人机群的编队控制。通过仿真结果中的编队误差和编队轨 迹验证了基于一致性和自抗扰的控制器有着更强的鲁棒性和抗干扰能力。
Multi-agent Formation Control Method Based on Consensus and Active Disturbance Rejection
WANG Huan
(School of Electrical Engineering and Control Science, Nanjing University of Technology, Nanjing Jiangsu 211816)
【Abstract】: Multi-agent cooperative formation problem is a hot topic in multi-agent research . In this paper, the formation control of a quadrotor UAV swarm in a disturbed environment is studied . Firstly, the time-varying formation control algorithm without disturbance is simulated . Then the active disturbance rejection control technique is proposed to suppress the disturbance due to the presence of the disturbance factor wind. Finally, the time-varying formation control algorithm and active disturbance rejection control technology are combined to realize the formation control of UAV swarm under disturbance environment . The formation error and formation trajectory of the simulation results show that the controller based on consistency and active disturbance rejection has stronger robustness and anti-interference ability.
【Key words】: multi-agent formation;active disturbance rejection control technology;algorithm of consistency
0 引言
在目前的技术水平下单智能体性能有限, 而多智能体 系统有着更强的容错性和更高的效率。多智能体编队控制 的经典方法有 3 种:领航跟随者法 [1]、基于行为法 [2]、虚 拟结构法 [3]。这些编队控制方法往往忽略了多智能体编 队中各个智能体之间的信息交互会对编队效果产生影 响。因此近年来一些学者开始采用一致性算法来解决编 队问题。文献 [4] 提出了多机器人编队控制的分布式协 调架构。文献 [5] 给出了无人机编队的分散轨迹规划器 的设计方法。在研究通过一致性算法来解决编队控制问 题的学者中,董希旺和他的团队在近些年来获得了很多 成果。文献 [6] 给出了基于输出反馈的编队控制方法, 文献 [7] 和文献 [8] 分别针对有向通信网络和无向切换通信网络设计了基于一致性的编队控制器。
虽然基于一致性的算法已经在编队控制问题中得到 广泛应用,但在无人机飞行过程中常常会受到外界阵风 以及空气阻力等因素的扰动,而这些扰动往往又难以进 行精准的建模分析。因此,考虑扰动环境下多智能体编 队控制问题具有现实意义。
针对扰动问题学者们列举了多种控制方法,在这些 方法中线性控制方法有 PID 控制 [9]、二次线性调节器控 制等,非线性控制方法有反步法、反馈线性化。本文选 用自抗扰技术来对扰动进行抑制。该方法简单有效,不 要求被控对象有精确的数学模型。自抗扰控制把实际对 象和标准控制模型的差看作广义的扰动 , 通过估计来补 偿,解决了系统的不确定性问题。
1 编队控制问题描述
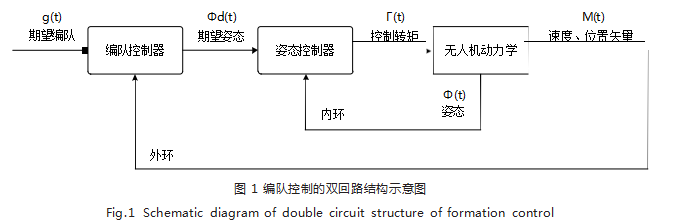
对于一个由多架无人机组成的无人机群系统,其中 每一架无人机的编队控制都可以分为两部分: 内环姿态 控制和外环轨迹控制。编队控制的双回路结构图如图 1 所示。
其中 g(t)、 Φd (t)、 Φ(t)、 Γ(t) 和 M(t) 分别 表示期 望 的编队、期望的姿态、编队中的姿态、控制转矩、位置 和速度矢量。本文主要研究的内容是外环轨迹控制结构 中的编队控制问题,内环姿态控制可以通过 PD 控制器 进行控制。对于无人机 i (i ∈ 1.2.… ,N)来说,它的外 环动力学方程可以近似描述为如式 (1) 所示:
其中xi (t) ∈ Rn , vi (t) ∈ Rn , ui (t) ∈ Rn 分别用于表示无人机的位置、速度和控制输入向量。如果在下文中没有特殊 说明,则 n=1.当 n ≠ 1 时可以用⊗符号表示 Kronecker 积直接推广到高维情况。N 架无人机之间的交换拓扑可以 用无向图G = {V, E, W} 表示,其中V = {v1 , v2 , ..., vN }表示节点 集, E ⊆ {(vi , vj ): vi , vj ∈V}是边缘集, W = [wij ] ∈ RN×N 是一个 具有非负元素的对称邻接矩阵。对于∀i, j ∈ {1.2. ..., N},无 人机 i,无人机j 可以用 V 中的 vi , vj 表示,无人机 i,无 人机j 之间的交互通道可以用 E 中的 eij=(vi,vj) 表示。如果 存在这么一条边 eji ,那么就可以称无人机j 是和无人机 i 相连的。定义拉普拉斯矩阵 L 为 L=D- W 来更好地描 述无人机群系统中各个无人机相互之间的邻居关系,其

中为度矩阵。对于一个无向图而言,如果每一个节点都有一条到任何其他节点的通 道,那么我们称这个无向图是连通的。文献 [10] 研究了 二阶连续时间多智能体系统一致性协议,如式(2)所示:
其中 γ 为协议参数,当通信拓扑图为无向连通图时,如果 γ > 0.则多智能体系统能够在协议的作用下达到 一致。
定义Mi (t) = [xi (t), vi (t)]T, B1 = [1.0]T 和B2 = [0.1]T ,那么无人机外环动力学方程(1)可以等价于如式(3) 所示:
M.i (t) = B1B2TMi (t)+B2ui (t) (3)
令g(t) = [g1T (t), g2T (t), ..., gNT ]T ∈ R2N 作为期望编队结果, 其中gi (t) = [gix (t), giv (t)]T (i ∈ 1.2. ..., N)作为分段连续可微向量。
多智能体协同控制的目标是使无人机群系统(3) 到达时变编队 g(t) 的状态。如果系统在控制量 ui (t) 的 作用下实现如式(4)所示的形式,令 r(t) 为编队中心, 那么就达成编队控制目标。
2 基于一致性的编队控制方法
文献 [8] 中提出了一种基于一致性方法的多智能体 编队控制方法:对于无人机群系统中的第 i 架飞机, 可 以考虑如(5)式所示的控制量:
其中K1 ∈ R1×2 和K2 ∈ R1×2 都是恒定增益矩阵, g.iv (t)是 目标编队的导数。增益矩阵 K1 的作用是指定时变编队 参考的运动模式。文献 [8] 中具体阐述了 K1 , K2 的值是 如何计算的。
通过 MATLAB R2019b 对以上控制律进行了模拟仿 真。选择四架无人机作为控制对象,通过控制律式(5) 实现如式(6)所示的时变编队控制。
其中r = 10m , ω = 0. 1rad/s。选择矩阵K1 = I2 ⊗[−1.−0.8] ,K2 = I2 ⊗[0.3535.0.6582] ,以确保无人机群系统能够达到 预期的编队,其中 I2 为 2 阶的单位矩阵。
选择四架无人机的初始状态为 [2.84.-2.11.2.19.2.07], [-2.41.-3.04.4.51.0.22],[-3.47.3.38.1.48.1.02],[-1.93.4 .08. 3.11.-2.25],同时在仿真中选取采样时间 T=0.05s。
通过如图 2 所示的编队位置仿真和如图 3 所示的编 队误差分析可以看出在没有扰动的情况下,无人机可以 通过式(5)中控制量 ui (t) 的作用使得误差趋于零,实 现编队。然而无人机编队过程中常常会面临风的扰动, 使得无人机位置发生瞬时的偏移,所以需要提高无人机 编队的系统的抗干扰能力。
3 基于自抗扰和一致性的多智能体编队方法
在没有扰动的情况下,外环动力学方程可以描述为 方程(1),但在实际情况下往往会存在扰动对控制量 ui 产生影响。因此建立在扰动下的外环动力学方程如 式(7)所示:
其中di (t) ∈ Rn 为实际情况中阵风对控制量产生影响的扰动。考虑到实际情况中风速等条件, di (t) 是一个可 微有界量。
因为误差难以建模且控制增益存在一定的不确定 性,文中采用自抗扰控制方法。自抗扰控制器的设计主 要包括 3 个部分 : 安排过渡过程、扩张状态观测器和状态误差反馈控制律。安排过渡过程目的降低初始误差 , 能降低初始阶段对系统的冲击。文中在编队控制初期选 择不采用误差较大的观测结果来对控制量 ui 进行调整, 这同样起到了降低误差的作用。
扩张状态观测器是自抗扰控制技术中最重要的一部 分,基于扩张状态观测器思想,我们可以利用一种特殊 的反馈机制将影响到系统最后被控输出的扰动扩张成一 种新的状态变量。对于本文中式(7)我们可以设计如 式(8)所示的扩张状态观测器:
其中 zi 1 (t) ∈ Rn , zi 2 (t) ∈ Rn , zi 3 (t) ∈ Rn , ei (t) ∈ Rn ,分 别为无人机 i (i ∈ 1.2.… ,N)当前状态的位置 x,速度 v,总扰动 d 的观测值, bi1.bi2.bi3 为可调增益。根据带宽 法,将 bi1.bi2.bi3 分别设为3ω0 ,3ω02 , ω03 。
通过扩张状态观测器对扰动进行估计之后,基于式(5)设计出对应的误差反馈控制律,如式(9)所示:
通过该控制律可以对扰动进行补偿。
通过 MATLAB R2019b 对以上观测器和控制律进 行了模拟仿真。用四架四旋翼无人机对扰动环境下的时 变编队进行模拟,期望达到的编队控制结果如式(10) 所示:
其中 r=10. ω=0.1.在仿真中选择四架四旋翼无 人 机 的 初 始 状 态 为 [2.84. -2.11. 2.19. 2.07],[-2.41.
-3 .04. 4 .51. 0 .22],[-3 .47. 3 .38. 1 .48. 1 .02],[-1 .93. 4.08. 3.11. -2.25], 选取采样时间 T=0.05s。同时假设 扰动di (t) = 2sin(t)。如图 4 所示无人机系统无法形成轨 迹圆编队,如图 5 所示无人机系统最终存在稳态误差。
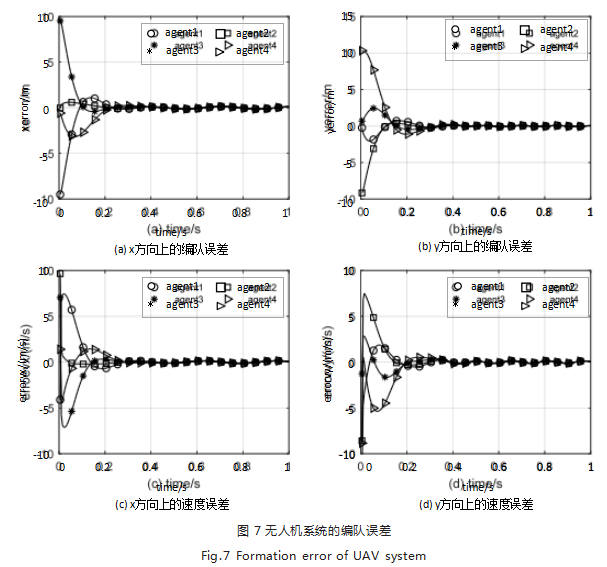
对于式(8), 将 bi1.bi2.bi3 的值分别设为3ω0 ,3ω02 , ω03 , 其中 ω0 的值设为 55.由编队位置曲线如图 6 所示可以 看出四架无人机最终收敛到轨迹圆上,由误差分析图 7可以看出无人机系统的编队误差最终收敛至有界。
4 总结
本文研究了四旋翼无人机编队控制问题,针对编队 过程中存在的阵风扰动,提出了基于一致性算法和自抗扰控制技术的编队控制方法。在一致性编队控制算法的 基础上,基于无人机动力学方程设计扩张状态观测器对 扰动进行估计并在控制器中对扰动进行抑制。仿真结果 表明,本文提出的控制方法能够使无人机系统实现规定 的编队轨迹,最终误差收敛至有界。由于设计的扩张状 态观测器能够实现对于系统扰动的有效估计,从而提高 了系统了抗干扰能力。针对于无人机的编队控制问题, 未来的研究工作将主要集中于提高无人机系统避障避碰 能力和轨迹规划能力。
参考文献
[1] 王晶,顾维博,窦立亚 .基于Leader-Follower的多无人机编 队轨迹跟踪设计[J].航空学报,2020.41(S1):88-98.
[2] 安永跃,李淑琴 .基于行为规划的多机器鱼编队策略的研究 [J].计算机仿真,2013.30(11):369-373.
[3] 李正平,鲜斌 .基于虚拟结构法的分布式多无人机鲁棒编队 控制[J].控制理论与应用,2020.37(11):2423-2431.
[4] WEI R,SORENSEN N . Distributed Coordination Architecture for Multi-robot Formation Control[J].Robotics & Autonomous Systems,2008.56(4):324-333.
[5] TURPIN M,MICHAEL N,KUMAR V.Decentralized Formation Control with Variable Shapes for Aerial Robots[C]//IEEE International Conference on Robotics & Automation.IEEE, 2012:23-30.
[6] DONG X,HU G .Time-varying Output Formation for Linear Multiagent Systems Via dynamic Output Feedback Control[J].IEEE Transactions on Control of Network Systems, 2015.4(2):236-245.
[7] DONG X,YU B,SHI Z,et al .Time-Varying Formation Control for Unmanned Aerial Vehicles:Theories andApplications[J].IEEE Transactions on Control Systems Technology,2014.23(1):340-348.
[8] A X D,B Y Z,A Z R,et al.Time-varying Formation Control for Unmanned Aerial Vehicles with Switching Interaction Topologies - ScienceDirect[J].Control Engineering Practice, 2016(46):26-36.
[9] MILHIM A,ZHANG Y,RABBATH C A.Gain Scheduling Based PID Controller for Fault Tolerant Control of Quad- Rotor UAV[C]//Aiaa Infotech,2010.
[10] LIU C L,FEI L .Consensus of Second-order Multi- agent Systems with Input Delay[C]//Chinese Control & Decision Conference,2010.
关注SCI论文创作发表,寻求SCI论文修改润色、SCI论文代发表等服务支撑,请锁定SCI论文网!
文章出自SCI论文网转载请注明出处:https://www.lunwensci.com/jisuanjilunwen/61597.html