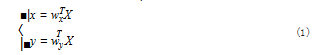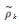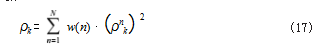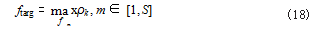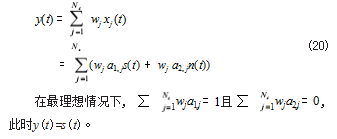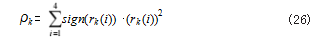SCI论文(www.lunwensci.com)
摘 要:稳态视觉诱发电位(Steady-State Visual Evoked Potential, SSVEP)作为一种特征较为明显的脑电信号,有着 训练迅速、数据集要求少、分类准确率高等优点,近年来广受关注。SSVEP 信号采集的过程中会受到环境、设备、人工操作 等因素的影响,因此模型对不同信噪比信号的稳定性显得尤为重要。本文提出一种空间滤波器组典型相关分析模型,在原始信 号、人工合成信号、平均特征信号三者之间提取四种空间滤波器用于后续分类,并将该模型与另外四种模型在不同信噪比情况 下进行对比分析。六组低信噪比数据集为采集数据、六组高信噪比数据集为清华数据集,实验证明该模型在使用高低信噪比数 据时均有优秀的分类性能,最高可达 99.24%,且对不同数据长度有较高鲁棒性,同时信息传递速率(Information Translate Rate, ITR)最高可达 105.1 bits/min。
SSVEP Signal Processing Based on Spatial Filter Banks Canonical Correlation Analysis
TANG Shize, ZHANG Xuejun, YANG Yi
(Nanjing University of Posts and Telecommunications, College of Electronic and Optical Engineering, College ofFlexible Electronics (Future Technology), Nanjing Jiangsu 210023)
【Abstract】: Steady-State Visual Evoked Potential, as an EEG signal with obvious characteristics, has the advantages of rapid training, less data set requirements, and high classification accuracy. It has been widely concerned in recent years. The SSVEP signal acquisition process will be affected by the environment, equipment, manual operation and other factors, so the stability of the model for signals with different SNR is particularly important. In this paper, a model of spatial filter banks canonical correlation analysis is proposed. Four spatial filters are extracted from the original signal, artificial reference signal and average characteristic signal for subsequent classification, and the model is compared with the other four models under different SNR. Six sets of low SNR datasets are collected data, and six sets of high SNR datasets are Tsinghua datasets. Experiments show that the model has excellent classification performance when using high and low SNR data, up to 99.24%, and has high robustness to different data lengths. At the same time, the ITR can reach up to 105.1 bits/min.
【Key words】: brain computer interface;spatial filter banks canonical correlation analysis;steady-state visual evoked potential
0 引言
近年来,随着脑机接口 [1] (BrainComputerInterface, BCI)的相关研究日趋成熟,脑电信号处理算法也在不 断更新 [2],提高系统准确性和信息传输速率的同时,扩 大其在各领域中的应用范围 [3]。脑机接口,又称“大脑端口”或“脑机融合感知”,是一种提取生物信号特征 并以此控制外部系统的方式。在医学领域, BCI 普遍 用于残障人士对辅助运动设备的控制。该人机交互的 理念首先由 Vidal 于 1973 年提出 [4],1977 年该研究团 队使用视觉诱发电位 (Visual Evoked Potential, VEP)来控制电脑屏幕上类似光标的物体 [5] ;Bozinovski、 Farwell 等人先后实现了使用 α 波控制物体运动 [6]、 P300 电位在屏幕上打字的复杂任务 [7]。
脑机接口一般分为侵入式、部分侵入式和非侵入 式三类。其中非侵入式 [8] 因其创伤小、数据采集 / 实时 部署较为便捷、价格低廉而受到相关从业者的深入研 究,但其缺点也较为明显,该方式一般采用头皮外信号 采集设备进行实验,输出的信号噪声较大,去噪难度较 高。脑电图 [9] (Electroencephalogram, EEG)、脑磁图 (Magnetoencephalography, EMG)、功能近红外光谱 [10] (functional Near-Infrared Spectroscopy, fNIRS) 和功能核 磁共振成像(functional Magnetic Resonance Imagine, fMRI) 等为常用的非入侵式信号获取方式, 其中 EEG 拥有无创、时间分辨率高等优点,是 BCI 应用中最常用 的获取中枢神经系统产生的活动电位的方法。根据是否 使用外部刺激, 可以将 EEG 信号分成两类 :第一类是非 外部刺激产生的信号 ( 内源性脑电 ),例如运动想象 [11] (Motor Imagery, MI)实验中,受试者主动想象不同 的动作来产生频带和振幅不相同的电位 ;第二类是由外 部刺激产生的信号(外源性脑电),常用的有视觉诱发电 位和 P300 电位,当大脑接受外部不同形式的声音、图 像刺激后,会有规律地在特定时间点产生不同幅度的电 位,而 BCI 系统正可以利用这些信息对外设进行控制。
视觉诱发电位 [12] 主要分为瞬时视觉诱发电位 (Transient Visual Evoked Potential, TVEP) 和稳态视 觉诱发电位(SSVEP)两类。当视觉获得一个外界恒定 频率的刺激时,与刺激频率或谐波频率相一致的神经网 络就会产生谐振,导致大脑的电位活动在刺激频率或谐 波频率处出现明显变化, SSVEP 信号由此产生,其最大 振幅集中在枕叶区,特征是在刺激频率及其谐波处出现 较为明显的波峰。基于 SSVEP 的 BCI 系统具有 ITR 高、 训练需求少等优点,因此在控制应用中被广泛使用。为了 解码 SSVEP 信号中受试者的意图,人们提出了多种方法 来识别与视觉刺激相对应的频率或相位成分, 如功率谱密 度分析 (Power Spectral Density Analysis, PSDA)、典型 相关分析 [13] (Canonical Correlation Analysis, CCA)、 多元同步指数 [14] (Multivariate Synchronization Index, MSI)、多元线性回归(Multiple Linear Regression, MLR)。 而 CCA 作为能从多通道数据中分析出对应频率的高鲁棒 性特征提取方式,深受各方研究者的喜爱,并大量作为 扩展算法的基础理论依据,如提取个体模板特征的典型 相关分析(IndividualTemplate-based CCA, ITCCA) [15]、 多重集典型相关分析(Multiset CCA, MsetCCA) [16]、L1 正则化多路典型相关分析(L1-regularized Multiway CCA, L1-MCCA) [17]。Chen 及其团队利用滤波器组对 原始信号进行子带分解,进一步提高了系统的性能,使 ITR 达到 5.32bit/sec[18]。SSVEP 信号特征提取的最新 研究方向是通过优化空间滤波器来增强 SSVEP 信号的 再现性, Zhang 等人提出了相关成分分析法来最大化不 同电极的相关性 [19] ;Nakanishi 等人提出了任务相关成 分分析法(Task-Related Component Analysis, TRCA) 来提高多通道 SSVEP 信号的信噪比(Signal-noise Ratio, SNR),ITR 被进一步提高 [20]。
与实验室低 / 无噪声环境相比,实际应用中外界干 扰尤为明显,且部分个体对频率刺激的敏感度较差,最 终获取的 EEG 信号信噪比较低。针对 SNR 不同的脑 电信号,本文提出一种鲁棒性较高的空间滤波器提取 算法,该算法需对离线数据进行训练。首先利用标准 CCA 最大化两组数据间的相关性,提取出训练信号与 人工合成信号的两种空间滤波器,其次用训练得到的空 间滤波器分别对测试信号和人工合成信号进行滤波,再 将滤波后的两组数据应用相关系数计算得出第一个相关 系数。同理提取训练信号和平均特征信号、训练信号和 人工合成信号、平均特征信号和人工合成信号的空间滤 波器,与第一类相比,这三类滤波器滤波对象为测试数 据和平均特征信号。最终计算获得的四个相关系数加权 平方求和,得到的结果用于比较分类。
训练信号及平均特征信号分别与人工合成信号所提 取的特征能提升低信噪比下的分类准确率,而训练信号 与平均特征信号提取的自特征能提高高信噪比下的分类 准确率。实验结果表明低信噪比情况下该模型准确率比 其他模型高,高信噪比情况下和 TRCA 等训练算法几 大致相等,且随着数据长度减小,该模型准确率衰减较 慢,综合 ITR 和准确率两方面来看,输入数据长度为 2s 时该模型性能最佳。
1 研究方法
1.1 典型相关性分析
假设两组多维向量需要检测成分相关性,若每次每 组各提取一个变量进行相关性分析,计算将变得冗长, 因此 CCA 采用的是主成分分析的思想, 即找到两组向 量之间相关性最大的线性组合,该线性组合的相关系数 可确定两组原向量间各成分的相关关系。
设两组多维向量为X ∈ Rk1×p 和 Y ∈ Rk2×p,线性组合系数为 wx ∈ Rk1×1 和 wy ∈ Rk2×1.则X 与 Y 的协方差矩阵为 :
则 λ 为矩阵 A 的特征值, 最大特征值对应的特征向 量即为使两组向量相关性最大的空间滤波器。
CCA 模型应用在 SSVEP 特征提取上时有两个输入 信号,一个是待分类的测试信号X,另一个是人工构造 的不同频率下的参考信号 Y,即 :
其中 Nh 为谐波数, fm 为目标频率, fs 为采样率, T为采样点数。
1.2 滤波器组典型相关分析
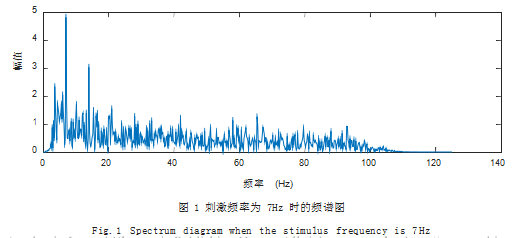
稳态视觉诱发电信号在基频区域的频谱中呈现出明显 的峰值, 且较高信噪比的数据在相应的倍频区域也呈现出 较高的波峰,但峰值会随着频率增加而下降。如图 1 所示 的频谱图中,主频 7Hz 及 14Hz、21Hz 都存在明显波峰 :
CCA 模型是对 SSVEP 信号整体进行的最大化相关 性处理,因而忽略了部分谐波分量信息,因此 Chen 及 其团队利用滤波器组对信号进行频带切割,依次滤除上 个子带最低频的主波或者谐波分量,只保留后面的高频 成分, 得到的 N 个子带与通过相同滤波器的参考信号进 行典型相关分析,最终得出加权后的分类依据
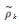
其中 N 个子带对应的相关系数权重为 :
w(n) = n−a + b, n ∈ [1. N] (16)
第 k 个刺激目标相关系数平方加权后得出的分类 依据 :
该模型对第 k 个刺激目标的分类频率为(共 S 个刺激频率) :
FBCCA 模型旨在最大化利用刺激信号的谐波分量, 并通过网格搜索法找出最佳的权重系数 a、b 值,从而 提高目标识别的准确率。
1.3 任务相关成分分析
CCA 和 FBCCA 都为非训练算法, 而 Nakanishi 及 其团队首次尝试将任务相关成分分析应用至 SSVEP 信号 分类上。该模型旨在找出一种线性组合,使得多个 trial 之间任务相关分量的复现性(reproducibility)最大 化,而信号中任务无关分量,即噪声得到抑制,以此来 提高数据的信噪比。该方式能很大程度上将脑电的背景活动影响降至最低。
假设某一多通道 SSVEP 的第j 个通道信号为 xj (t), 其中包含了任务相关成分 s(t) 和任务无关成分 n(t),则
xj (t) = a1.js(t) + a2.jn(t), j = 1. 2. ..., Nc (19)
其中 a1.j、a2.j 为组合系数, Nc 为通道数。
为了提取任务相关成分,先对信号的各个通道求和
该边界问题可通过协方差最大化 (CovMax) 或相关 性最大化 (CorrMax) 求解。相关性最大化的解不是封 闭解,只能得到一个任务相关成分,因此一般采用协方 差最大化。
求出的最大特征值对应的特征向量作为空间滤波器, 设第 m 个子带第 n 个刺激 的空 间滤波器为 wn(m),则训练信号Xn(m) 和平均模板信号Xn(m) 间的相关系数为 :
r(nm) = ρ((X(m) )T w(nm) , (X(nm) )T w(nm) ) (21)
2 空间滤波器组典型相关分析
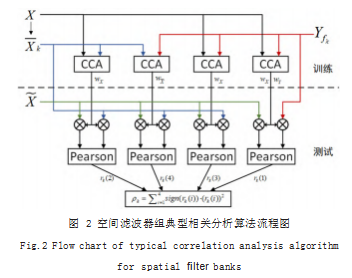
本文提出一种空间滤波器组典型相关分析法(Spatial Filter Bank Canonical Correlation Analysis, SFBCCA) 对多组 SSVEP 信号进行分析,算法流程如图 2 所示。 SFBCCA 方法对多组不同输入进行训练,提取的特征 (即空间滤波器)用于平均特征信号和测试信号的滤波, 滤波后的信号计算皮尔逊系数,得出的多个值加权平方后求和得出分类依据 ρk(n)。
四组训练中第 k 个目标的分类结果分别为 :
(1)标准 CCA,提取训练信号X 和人工合成信号Yf k 的空间滤波器 wX、wY,两个空间滤波器分别滤波测试信号 X 和 Yf k试信号 X 和 Yf k
rk (1) = ρ (XT wX (X, Yfk ), Yfk(T)wY (X, Yfk )) (22)
(2) 训练数据驱动型 CCA[21] (Training Data-drivenCanonical Correlation Analysis, tdCCA), 提取训练信号X 和平均特征信号Xk 的空间滤波器 wX、wX(_),仅使用 wX 对 X 和 Xk 进行滤波
rk (2) = ρ (XT wX (X, Xk ), XTkwX (X, Xk )) (23)
(3)提取训练信号 X 和人工合成信号 Yf k 的空间滤波器 wX、wY,仅使用 wX 对 X 和 Xk 进行滤波
rk (3) = ρ (XT wX (X, Yfk ), XTkwX (X, Yfk )) (24)
(4) 提取平均特征信号Xk 和人工合成信号 Yf k 的空间滤波器 wX_、wY,仅使用 wX_ 对 X 和 Xk 进行滤波
rk (4) = ρ (XT wX (Xk , Yfk ), XTkwX (Xk , Yfk )) (25)
对于信噪比低的信号,鲁棒性较差的特征在频率识 别过程中会导致 ρ 值偏低,而鲁棒性高的特征则会使模 型输出高 ρ 值,因此平方求和能更好检测出目标刺激 :
最终模型识别出的测试信号ft 的频率为 :
ft = arg maxρk , f = f1 , f2 , ..., fn (27)
3 数据采集及预处理
本文使用美国 Neuroscan 公司的脑电信号采集系统。为了避免谐波对频率识别造成的干扰,刺激频率为非 整数倍关系, 选用 5Hz、6Hz、7Hz、8Hz、9Hz、11Hz、 13Hz、17Hz 这 8 个频率。实验中采集的电极有 P3、 P4、PO3、PO4、O1、O2、Pz、Oz、T5、T6.后续分 析发现枕叶区的 8 个电极(P3、P4、PO3、PO4、O1、 O2、Pz、Oz) 记录的 SSVEP 信号特征较为明显,故选 用这 8 个电极作为信号处理的原始数据。脑电信号采集 过程中电极的阻抗均保持在 10kΩ 以下,采样率为 500 Hz,使用 50Hz 的陷波器消除工频干扰。数据进行特征 提取前通过了 3Hz 至 110Hz 的带通滤波器,滤波器为 切比雪夫 I 型。
实验邀请 6 名年龄在 21 ~ 23 周岁的受试者进行实 验,实验前均无受过相关训练,视力校正后均正常,受 试者眼睛距视觉刺激约 0.4 m。实验范式采用 E-Prime 2.0 进行设计, 刺激界面如下图所示, 每个频闪画面随 机单独播放 8s,每一轮 8 种刺激全部出现一次,循环 10 次。考虑到不同受试者眼部对刺激的敏感度不同, 每两个刺激间隔 8 s。
4 实验结果与分析
本文针对 FBCCA 设计了滤波器组以适应采集的数 据集 :数据带宽为 12Hz,则第个子带下限频率为 Hz, 即 5Hz、17Hz、29Hz、41Hz、53Hz、65Hz、77Hz、 89Hz,上限频率为 99Hz,考虑到切比雪夫 I 型滤波 器阻带衰减速度,通带两边分别预留 2Hz 及以上额外 带宽,例如本文设计的第一个滤波器阻带上下限应为 [3Hz,109Hz],通带为 [5Hz,99Hz]。
采用留一交叉验证评估模型性能,即数据集中每 个 trial 均作为测试集一次,其余作为训练集训练特征。 验证重复 10 次,准确率为 10 次分类结果的平均值。
4.1 低信噪比数据模型性能对比
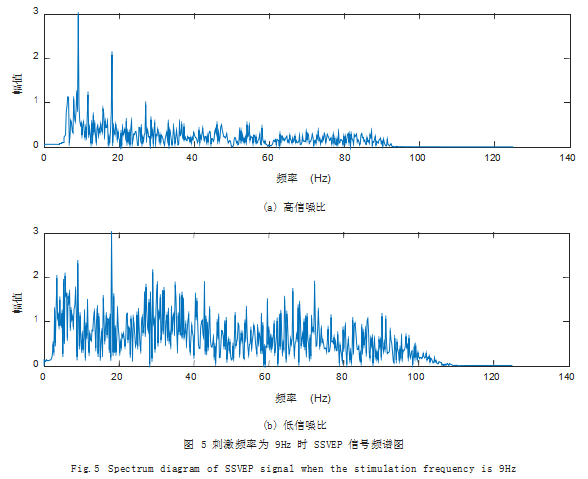
如图 5 所示,在相同刺激频率下,高信噪比信号频 谱特征为基波和谐波处有较高波峰且其他频率幅值较 低,而低信噪比信号在非基波和谐波处普遍存在较高的 幅值,该现象会直接影响后续的特征提取,因此模型的 高鲁棒性显得尤为重要。
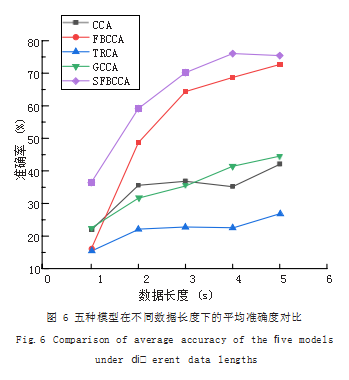
本节新增广义典型相关分析(Generalized Canonical Correlation Analysis, GCCA) [22] 进行对比。该模型 为典型相关性分析的广义扩展,该方法确定了一种线性 变换,使多组变量之间的相关性最大化。图 6 所示为 CCA、FBCCA、TRCA、GCCA、SFBCCA 这五种模型在 1-5s 的平均准确率。在每一数据长度上 SFBCCA 的 性能均最好, 其次为 FBCCA,CCA 和 GCCA 性能相 当, 而 TRCA 性能最差。FBCCA、GCCA 及标准 CCA这三个模型都使用正余弦信号作为参考信号进行特征提 取, TRCA 则是通过降噪后自特征提取来实现分类,说 明在低信噪比信号中,仅通过自身信号来完成全部特征 提取无法达到高分类效率,而人工合成信号能大幅提升 模型性能,因此本文提出的 SFBCCA 模型使用到三种 带有人工合成信号的特征提取方式计算相关系数。
SFBCCA 为非子带分解的训练算法,准确率在数据 长度为 4s 时已达最大, 5s 时准确率略有下降,其余四 个模型均在 5s 达到最大值,说明同比与其他模型,低 信噪比时 SFBCCA 能利用更短的数据达到最佳的分类 准确率。通过比较图 5 可知,信号信噪比较低时,倍频 周围峰值过多,导致子带分解后提取的特征不准确,而 权重系数给予后面子带的权重过高导致准确率低,若不 断减小后面子带的权重就将和 CCA 无差别, 且针对不 同信噪比寻找权重系数不利于应用,因此非子带分解的 模型在低信噪比特征提取优势较大。
信息传输率(ITR) 为衡量 BCI 系统中数据传输速度的重要指标,计算公式为 :
ITR = [log2 N + P log2 P + (1− P) log2 1 − P ] ⋅ 60 (28)
其中 N 为刺激数量, P 为分类准确率, T 为单次目标选择时间。
刺激数量和单次目标选择时间相同的情况下, 仅分类 准确率影响 ITR 大小,因此只对比 SFBCCA 和 FBCCA 的 ITR :
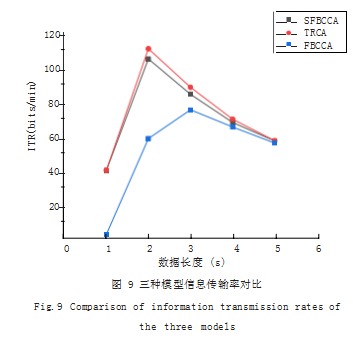
SFBCCA 模型 ITR 比 FBCCA 平均高 7.58bits/min, 且能更快(2s 时)达到 ITR 峰值,说明该模型有着更 好的信息传输能力。
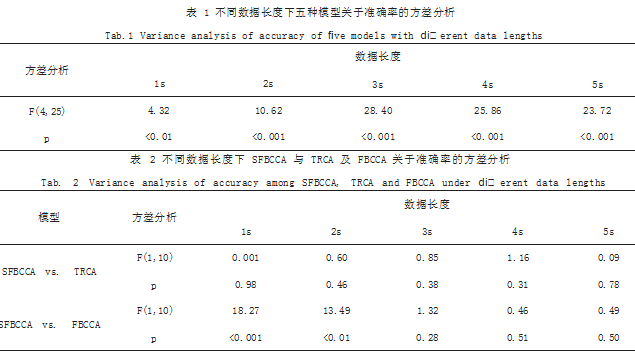
通过单因素方差分析(One-way ANOVA),在所 有数据长度下,除 1s 外,所有 p 值均小于 0.001.说 明五种方法的准确率存在显著差异,表 1 为统计分析的结果。此外,将 SFBCCA 与其他每个模型单独进行方 差分析后发现, p 值均小于 0.001.说明 SFBCCA 与其 他模型准确率差异显著,低信噪比情况下性能远好于其 他模型。
4.2 高信噪比数据模型性能对比
本节采用清华大学脑机接口研究组官方网站下载 的 6 组 SSVEP 数据集 [23],该数据集被广泛应用于各种 SSVEP 信号的研究,很多文献都证明该数据集具有较 高的信噪比。
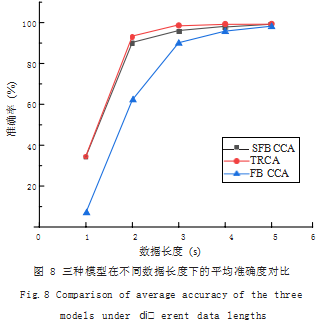
图 8 中 SFBCCA 和 TRCA 准确率曲线几乎重合, 两者平均只相差 1.5%,且数据长度 2 s 及以上的准确率能够达到 90% 以上,数据长度为 5 s 时分别达到 99.24%、99.37%, 表明在高信噪比条件下,TRCA 能 够较好地提取自身特征,且 SFBCCA 拥有足够优秀的 分类性能。FBCCA 随数据长度减少,分类性能迅速下 降,而其他两种训练算法则保持缓慢下滑,平均准确率 远高于 FBCCA,体现了训练算法对于数据长度的高鲁 棒性。
5s 数据长度时三种模型准确率在 99% 左右,因此 ITR 相近, 但由图 9 可知, 低于 5s 时 SFBCCA 与 TRCA 的信息传输性能均好于 FBCCA,且在 2s 时 ITR 达到 最大,实际应用中可将 2s 作为切分数据的依据。
由表 2 可知, SFBCCA 与 TRCA 在各数据长度下 差异性不大(p>0.05), 说明在高信噪比情况下两模型 性能相近,而 SFBCCA 与 FBCCA 在 1、2s 时差异显著 (p<0.01),说明 SFBCCA 在此时间窗口下性能远好于 FBCCA,符合图 8 的准确率曲线。
5 结论
不同的 SSVEP 分类模型对数据长度、信号信噪比 的鲁棒性不同。在低信噪比情况下, TRCA、GCCA 准 确率偏低, 而高信噪比时 TRCA 准确率较高, 说明训 练算法对信号噪声敏感度较高。非训练算法如 CCA、 FBCCA,对噪声相对不敏感,但数据长度对该种算法 的准确率有很大影响。本文提出的 SFBCCA 同时利用 人工合成信号和自身的平均特征信号的特征信息,使得 模型在高低信噪比时都有较为出色的分类准确率,且作 为训练算法能极大降低数据长度对分类精度的影响。但 该模型在 1s 时准确率还有提升空间,可后续改进。
参考文献
[1] WOLPAW J R,BIRBAUMER N,HEETDERKS W J,et al. Brain-computer Interface Technology:A Review of the First International Meeting[J].IEEE Transactions on Rehabilitation Engineering,2000.8(2):164-173.
[2] JIN J,MIAO Y,DALY I,et al.Correlation-based Channel Selection and Regularized Feature Optimization for MI- based BCI[J].Neural Networks,2019.118:262-270.
[3] ROCHA T,CARVALHO D,LETRA P,et al .BCI: Technologies and Applications Review and Toolkit Proposal[C]//International Conference on Multimedia Communications,Services and Security,2022:126-143. [4] VIDALJJ.Toward Direct Brain-computer Communication [J].Annual Review of Biophysics and Bioengineering,1973. 2(1):157-180.
[5] VIDAL J J.Real-time Detection of Brain Events in EEG[J].Proceedings of the IEEE,1977.65(5):633-641.
[6] BOZINOVSKI S,SESTAKOV M,BOZINOVSKA L.Using EEG Alpha Rhythm to Control a Mobile Robot[C]// Proceedings of the Annual International Conference of the IEEE Engineering in Medicine and Biology Society, 1988:1515-1516.
[7] FARWELL L A,DONCHIN E.Talking off the Top of Your Head:Toward a Mental Prosthesis Utilizing Event- related Brain Potentials[J].Electroencephalography and Clinical Neurophysiology,1988.70(6):510-523.
[8] PRESACCO A,FORRESTER L,CONTRERAS-VIDAL J L. Towards a Non-invasive Brain-machine Interface System to Restore Gait Function in Humans[C]//2011 Annual International Conference of the IEEE Engineering in Medicine and Biology Society,2011:4588-4591.
[9] GU X,CAO Z,JOLFAEI A,et al.EEG-based Brain- computer Interfaces (BCIs):A Survey of Recent Studies on Signal Sensing Technologies and Computational Intelligence Approaches and Their Applications[J]. IEEE/ ACM Transactions on Computational Biology and Bioinf ormatics,2021.18(5):1645-1666.
[10] ABDALMALAK A,MILEJ D,YIP L,et al.Assessing Time-resolved fNIRS for Brain-computer Interface Applications of Mental Communication[J].Frontiers in Neuroscience,2020:105.
[11] ZHANG K,ROBINSON N,LEE S-W,et al.Adaptive Transfer Learning for EEG motor Imagery Classificationwith Deep Convolutional Neural Network[J].Neural Networks,2021.136:1-10.
[12] GAO Z,DANG W,LIU M,et al.Classification of EEG signals on VEP-based BCI systems with broad learning[J].IEEE Transactions on Systems,Man,and Cybe rnetics:Systems,2020.51(11):7143-7151.
[13] LIN Z,ZHANG C,WU W,et al.Frequency Recognition Based on Canonical Correlation Analysis for SSVEP-based BCIs[J].IEEE Transactions on Biomedical Engineering, 2006.53(12):2610-2614.
[14] ZHANG Y,XU P,CHENG K,et al .Multivariate Synchronization Index for Frequency Recognition of SSVEP-based Brain – computer Interface[J].Journal of Neuroscience Methods,2014.221:32-40.
[15] BIN G,GAO X,WANG Y,et al.A high-speed BCI Based on Code Modulation VEP[J].Journal of Neural Engineering, 2011.8(2):025015.
[16] ZHANG Y,ZHOU G,JIN J,et al.Frequency Recognition in SSVEP-based BCI Using Multiset Canonical Correlation Analysis[J].International Journal of Neural Systems,2014. 24(04):1450013.
[17] ZHANG Y,ZHOU G,JIN J,et al.L1-regularized Multiway Canonical Correlation Analysis for SSVEP-based BCI[J]. IEEE Transactions on Neural Systems and Rehabilitation Engineering,2013.21(6):887-896.
[18] CHEN X,WANG Y,NAKANISHI M,et al.High-speedSpelling with a Noninvasive Brain–computer Interface[J]. Proceedings of the National Academy of Sciences,2015. 112(44):E6058-E6067.
[19] ZHANG Y,GUO D,LI F,et al.Correlated component Analysis for Enhancing the Performance of SSVEP- based Brain-computer Interface[J].IEEE Transactions on Neural Systems and Rehabilitation Engineering,2018. 26(5):948-956.
[20] NAKANISHI M,WANG Y,CHEN X,et al.Enhancing Detection of SSVEPs for a High-speed Brain Speller Using Task-related Component Analysis[J].IEEE Transactions on Biomedical Engineering,2017.65(1):104-112.
[21] WEI Q,ZHU S,WANG Y,et al.A Training Data-driven Canonical Correlation Analysis Algorithm for Designing Spatial Filters to Enhance Performance of SSVEP-based BCIs[J].International Journal of Neural Systems,2020.30 (05):2050020.
[22] SUN Q,CHEN M,ZHANG L,et al.Improving SSVEP Identification Accuracy Via Generalized Canonical Correlation Analysis[C]//2021 10th International IEEE/ EMBS Conference on Neural Engineering(NER),2021:61- 64.
[23] WANG Y,CHEN X,GAO X,et al.A Benchmark Dataset for SSVEP-based Brain – computer Interfaces[J].IEEE Transactions on Neural Systems and Rehabilitation Engi neering,2016.25(10):1746-1752.
关注SCI论文创作发表,寻求SCI论文修改润色、SCI论文代发表等服务支撑,请锁定SCI论文网!
文章出自SCI论文网转载请注明出处:https://www.lunwensci.com/jisuanjilunwen/61160.html