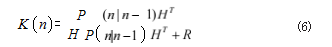SCI论文(www.lunwensci.com)
摘 要:基于非线性回归对目标航迹进行准确预测是实现目标跟踪的基础。针对传统的卡尔曼滤波在目标行为发生较快变 化时航迹预测精度降低的问题,本文提出了一种改进的卡尔曼滤波算法对目标航迹进行预测。该方法结合了目标的实际运动情 况,根据预测值和真实值的实时偏差调整滤波过程,将系统方差矩阵转换为可变量,从而可以解决当目标行为明显变化时传统 方法预测精度低的问题。实验结果表明,在目标行为状态发生变化的情况下,提出的算法均可以实现对目标航迹的速度、方向 和转向角的精准预测。
Target Track Prediction Algorithm Based on Historical Direction-finding Data
ZHAO Jingzhe1. TIAN Han1. ZHAO Liqing2. WANG Yuan2.3
(1.The 27th Research Institute of China Electronics Technology Group Corporation, Zhengzhou Henan 450047;2.State Key Laboratory of Networking and Switching Technology, Beijing University of Posts and Telecommunications,Beijing 100876;3.School of Systems Science, Beijing Normal University, Beijing 100875)
【Abstract】: Accurate prediction of target track based on nonlinear regression is the basis of target tracking. Aiming at the problem that the traditional Kalman filter reduces the accuracy of the track prediction when the target behavior changes rapidly, this paper proposes an improved Kalman filter algorithm to predict the target track. The method combines the actual motion of the target, adjusts the filtering process according to the real- time deviation of the predicted value and the real value, and converts the system variance matrix into a variable, which can solve the problem of low prediction accuracy of traditional methods when the target behavior changes significantly. The experimental results show that the proposed algorithm can accurately predict the speed, direction and steering angle of the target track when the behavior state of the target changes.
【Key words】: nonlinear regression;track prediction;kalman filtering
0 引言
无源定位系统通过对观测数据的综合处理,实现对 目标的航迹预测。目标航迹可以全面地反映出目标的运 动特征,方便对目标进行监管,而基于非线性回归对目 标航迹进行准确预测是实现目标跟踪预测的基础。
在工程应用领域,对航迹预测算法的研究受到了广 泛的关注。滤波算法是目标航迹预测和跟踪的关键技 术。如基于粒子滤波和卡尔曼滤波的算法在无人机、雷 达航迹预测与多目标跟踪中得到了有效应用 [1.2.9]。众多学者根据不同的应用场景对卡尔曼滤波算法进行了改 进。基于多项式卡尔曼滤波对船舶航迹预测,具有实 现简单、收敛迅速的优点 [3]。基于卡尔曼滤波算法的 ADS-B 航迹预测方案具有很好的航迹预测效果 [4]。基于 卡尔曼滤波在视景仿真环境下运动目标的航迹预测可以 满足航迹预测的精度需求 [5]。卡尔曼滤波对航空器的航 迹预测,将卡尔曼滤波与运动方程相结合对目标位置进 行跟踪预测, 均在实际系统中得到了应用 [6.7]。相比于 传统的轨迹预测算法,基于卡尔曼滤波的动态航迹预测算法具有更高的预测精度 [8]。
综上所述,卡尔曼滤波算法是目标航迹预测和跟踪 的关键技术,当系统的随机量服从正态分布时具有较好的 滤波效果 [10]。而当目标的航速、航向变化速度较快时, 传统的卡尔曼滤波的预测精度会明显降低,因此本文提 出了一种改进的卡尔曼滤波算法对目标航迹进行预测。
本文提出的方法结合了目标的实际运动情况,将系 统方差矩阵作为变量,根据预测值和真实值的实时偏差 调整滤波过程,从而可以提升预测精度,解决当目标状 态变化较快时传统方法预测精度低的问题。
1 目标航迹预测算法
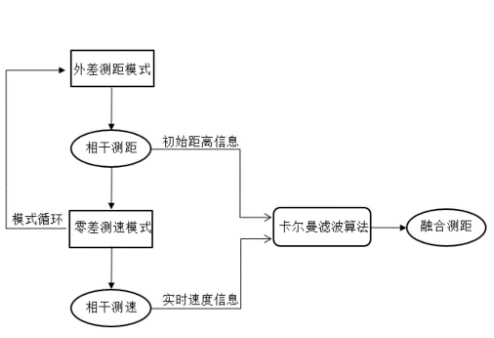
1.1 算法流程
本文提出了一种改进的卡尔曼滤波算法对目标航迹 进行预测,通过无源测向历史数据实现对目标的航迹速 度、方向和转向角的精准预测。具体流程如下 :
(1)首先需要将经纬度坐标转换成算法需要的直角 坐标系,同时算法中出现的速度参数也同样进行转换 , 这是由于经纬度与算法需要的平面直角坐标系不同 ;
(2)初始化卡尔曼滤波模型,用于后续操作 ;
(3)输入历史航迹点,同时执行改进的卡尔曼滤波 模型的更新模型操作,不断对模型进行优化 ;
(4)最后输入预测的时间点,利用模型得到预测航 迹点。
1.2 坐标转换
假设历史航迹点经纬度坐标为(λ,φ), 大地平面直角坐 标系原点 O 的坐标为(λ0 ,φ0 ),目标船舶的坐标为(x,y)。 其中正东方向为 Y 轴,正北方向为 X 轴,地理坐标转换 为大地平面直角坐标,即(λ,φ)→ (x,y)。本文采用如公 式 (1)、公式 (2) 所示的高斯 - 克吕格投影系统 (Gauss- Kruger Projection) 将经纬度转换为大地平面直角坐标。
其中 :∆λ= λ-λ0 , X = X (ϕ)-X(ϕ0 ) ,高度转变为 z 坐标值。
1.3 卡尔曼滤波
卡尔曼滤波算法是一种线性最优滤波算法,特点是 预测估计采用递归技术,无需考虑预测前的多个输入参数,重点关注前一时刻的状态参数进行预测。卡尔曼滤 波分为 2 个关键步骤,预测 (Predict) 和校正 (Correct)。 预测是基于上一时刻状态估计当前时刻状态,而校正则 是综合当前时刻的估计状态与观测状态,估计出最优的 状态,过程如下 :
(1)先验估计 :
X (n|n − 1)= AX (n − 1|n − 1)+ B (n|n − 1)* w(n − 1) (3)
(2)误差协方差 :
P (n|n − 1)= AP(n − 1 | n −1)AT (4)
(3)建立测量方程 :
Z (n)= H (n)X (n)+v (n) (5)
(4)计算卡尔曼增益 :
(5)修正估计 :
X(n | n) = X(n | n −1) + K (n) ■Z (n)− HX (n|n − 1)■ (7)
(6)更新误差协方差 :
P (n|n)= ■1 − K (n)H (n)■ P (n|n − 1) (8)
卡尔曼滤波根据系统的状态方程和观测方程,估计动态系统下一时刻的状态 :
Xˆ (n)= A (n|n − 1)X (n − 1)+ B (n|n − 1)w (n − 1) (9)
Z (n)= H (n)X (n)+v (n) (10)
X (t )是 n 维状态向量,描述 t 时刻的运动系统的每 个量的值 ;A (n|n − 1)为状态转移矩阵 ;Xˆ (n)是 n 时刻 的状态估计值 ;w (n − 1)表示运动模型的系统噪声,是 p 维零均值的白噪声 ;B (n|n − 1)是 n×p 维的干扰输入 矩阵 ;Z (n)表示观测向量,表示 n 时刻的系统观测值 ; H (n)是观测矩阵 ;v (n)表示观测噪声。
系统噪声w (n)和观测噪声v (n)是相互独立的高斯 白噪声, Q (n)是系统噪声w (n)的方差矩阵, R (n)是观 测噪声v (n)的方差矩阵。
1.4 改进卡尔曼滤波算法
传统的卡尔曼滤波理论通常假定系统方差矩阵Q(n)、 观测噪声方差矩阵R(n)是恒定的。但在实际中, 目标 航迹预测与跟踪系统是非线性的, Q (n)和R(n)都会随 着研究对象的运动而动态变化。R (n)主要由测量仪器 本身决定,而Q(n)则是不确定的。尤其当目标航速、航 向等运动状态变化速度较快时, Q (n)的变化对预测效果 的影响很大,而在传统卡尔曼滤波中通常假定Q(n)固定不变,导致预测精度受到限制。因此,本文提出了一种 改进的卡尔曼滤波算法预测目标航迹。本算法根据前一 时刻预测值和真实值的偏差对滤波过程进行及时的实时调整,更新 B(n | n - 1)Q(n - 1)BT (n | n - 1) 的值,以达到理想的预测效果,进一步提升预测精度。
B(n | n −1)Q (n- 1)BT (n | n- 1) = P(n | n- 1)- A(n | n- 1)P(n- 1 | n- 1)AT (n | n- 1) (11)
P(n | n- 1) = - ■K (n)H (n)- I ■− 1
K (n)R (n) · H (n) ■HT (n)H (n)■+ (12)
其中 [ · ]+ 表示广义逆矩阵。
将式 (12) 代入式 (11) 可得 :
B(n | n −1)Q(n −1)BT (n | n −1) = − ■K (n)H (n)− I ■− 1
K (n)R (n)H (n) ■HT (n)H (n)■+ − (13)
A(n | n −1)P(n − 1 | n −1)AT (n | n - 1)
由于状态估计值X(n | n)对下一时刻预测值的影响很 大,为提高预测精度,本文假设式 (8) 中X(n | n) = Xr (n), 其中Xr(n)表示 n 时刻航迹点的真实位置信息。由此可得 :
K *(n)= [Xr (n)- X(n | n - 1)]
[Z (n)- H (n)X(n | n - 1)]T (14)
然后,通过将式 (14) 替换式 (13) 得到 B(n | n- 1) Q (n- 1)BT (n | n- 1) 的值。为便于描述,将 B(n | n- 1) Q (n- 1)BT (n | n- 1)作为改进卡尔曼滤波算法的系统噪声。
1.5 预测建模
在t 时刻目标的空间位置、速度分别为(x (t ), y (t ), z (t )) 和(Vx (t ), Vy (t ), Vz (t ))。而加速度(ax (t ), ay (t ), az (t ))则通过目标 t-1 时刻和 t 时刻的速度求出,则目标在 t 时刻的 运动状态向量如下 :
X (t )= ■x (t ), y (t ), z (t ), Vx (t ), Vy (t ), Vz (t ), ax (t ), ay (t ), az (t )■T (15)
观测向量 :
Z (t )= ■x (t ), y (t ), z (t ), Vx (t ), Vy (t ), Vz (t )■T (16)
状态转移矩阵 :
观测噪声 R(n) 由观测设备决定。
然后根据历史航迹点依次得到对应时间点的观测值, 并依据此观测值和对应估计值进行模型调整,不断优化 模型,最后输入预测的时间,得到指定的预测航迹点。
2 仿真结果
实验分别使用 3 个、4 个、5 个历史测向数据预测 目标航迹。
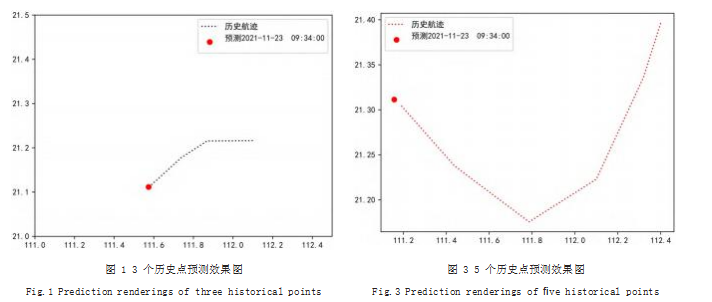
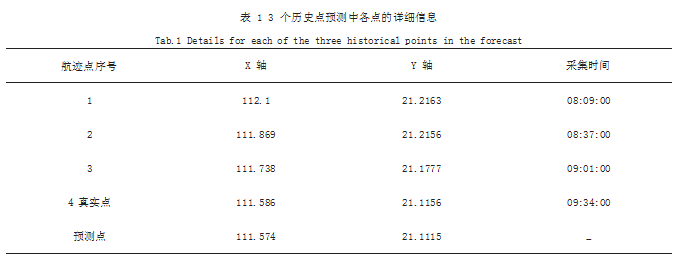
(1)基于 3 个历史测向数据对目标航迹进行预测, 详细信息如表 1 所示,其中航迹点 1-3 为历史测向数 据,航迹点 4 为预测时刻的真实值。实验使用提出的改 进卡尔曼滤波算法对航迹进行预测,从表 1 和图 1 可 知,预测点的位置与真实点的位置十分接近,在 X 轴和Y 轴上分别仅相差 0.012、0.0041.提出的算法可以对 目标航迹进行精准预测,这也说明预测过程中的中间结 果(目标方向、转向角)也是准确的。
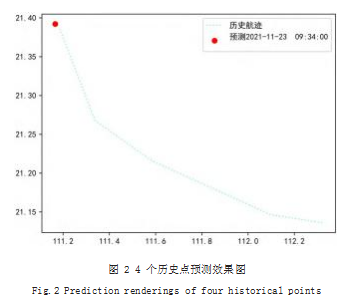
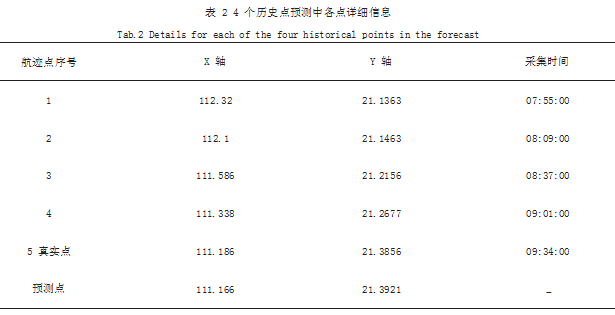
(2)基于 4 个历史测向数据对目标航迹进行预测, 详细信息如表 2 所示,其中航迹点 1-4 为历史测向数 据,航迹点 5 为预测时刻的真实值。从表 2 和图 2 可 知,预测点的位置同样与真实点的位置十分接近,在 X 轴和 Y 轴上分别仅相差 0.02、0.0065.
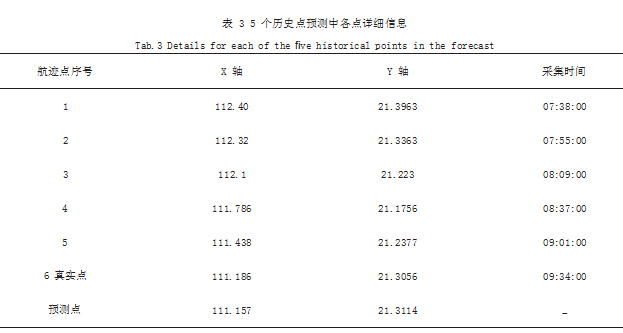
(3)基于 5 个历史测向数据对目标航迹进行预测, 详细信息如表 3 所示,其中航迹点 1-5 为历史测向数 据,航迹点 6 为预测时刻的真实值。从表 3 和图 3 可 知,预测点的位置与真实点的位置在 X 轴和 Y 轴上分 别仅相差 0.029、0.0058.提出的算法同样可以对目标 航迹进行精准预测。
综上所述,当目标的航速、航向发生变化时,文中 提出的改进卡尔曼滤波模型可以通过历史测向数据实现 对目标的航迹速度、方向和转向角的精准预测,从而为 目标航迹跟踪和预测提供基础。
3 总结与展望
针对传统的卡尔曼滤波在目标行为发生较快变化时 航迹预测精度降低的问题,本文提出了一种改进的卡尔 曼滤波算法,该算法根据预测值和真实值之间的实时偏 差对滤波过程进行实时调整,将系统方差矩阵转换为可 变量,更符合目标的非线性运动状态,能够提高目标行 为快速变化时的航迹预测精度。最后通过实验表明,在 目标运动状态发生快速变化的情况下,本文提出的算法 可以基于无源测向历史数据实现对目标的航迹速度、方 向和转向角的精准预测。在未来的工作中,我们需要结 合现阶段流行的时序型网络进行航迹预测。
参考文献
[1] 刘志花,李淑芬,李宝安.基于粒子滤波的无人机航迹预测方 法研究[J].电子测量与仪器学报,2010.24(7):643-649.
[2] 李天成,范红旗,孙树栋.粒子滤波理论、方法及其在多目标 跟踪中的应用[J]. 自动化学报,2015.41(12):1981-2002.
[3] 姜佰辰,关键,周伟,等.基于多项式卡尔曼滤波的船舶轨迹预 测算法[J].信号处理,2019.35(5):741-746.
[4] 卢献宇,张媛媛.基于卡尔曼滤波算法的ADS-B航迹预测[J]. 现代信息科技,2021.5(8):48-50+53.
[5] 张萍萍,孙永侃,李雪飞.视景仿真环境下基于卡尔曼滤波的 运动目标航迹预测方法[J].兵工自动化,2013.32(5):40-42+45. [6] 冯志轩.基于卡尔曼滤波的航迹预测探析[J].甘肃科技纵 横,2019.48(3):33-36.
[7] 王妍,邓庆绪,刘赓浩,等.结合运动方程与卡尔曼滤波的动态 目标追踪预测算法[J].计算机科学,2015.42(12):76-81.
[8] 乔少杰,韩楠,朱新文,等.基于卡尔曼滤波的动态轨迹预测算 法[J].电子学报,2018.46(2):418-423.
[9] 郑彩云.基于卡尔曼滤波的雷达航迹跟踪算法的综述[J].科 技视界,2019(11):33-34.
[10] 薛长虎,聂桂根,汪晶.扩展卡尔曼滤波与粒子滤波性能对 比[J].测绘通报,2016(4):10-14.
关注SCI论文创作发表,寻求SCI论文修改润色、SCI论文代发表等服务支撑,请锁定SCI论文网!
文章出自SCI论文网转载请注明出处:https://www.lunwensci.com/jisuanjilunwen/61102.html