SCI论文(www.lunwensci.com)
摘 要:研究小世界网络参数的改变对神经元网络放电特性的影响会对癫痫等神经疾病的研究工作产生重要的推动作用。 癫痫等神经疾病的发作总会伴随着神经网络的同步放电现象,目前神经网络的研究主要是基于层级网络,其拓扑结构不能模拟 真实生物神经网络,而小世界网络具有一定的生物神经网络特性,对小世界神经网络的仿真分析可以使仿真结果更贴近真实 生物的神经网络放电情况。通过构建小世界网络,进而基于 Izhikevich 神经元模型、短期突触可塑性调节机制和突触动力学 构建了小世界神经网络,并从兴奋性神经元和抑制性神经元的放电模式、放电栅图、平均放电频率和网络整体的放电同步性四 个方面进行分析。
关键词:Izhikevich神经元模型,小世界网络,短期突触可塑性,仿真分析
Study on Discharge Characteristics Based on Small World Neural Network
SONG Runhao, RUAN Yihui, CAO Hanwen, ZHANG Yifei, XU Linhua
(School of Electrical Engineering, Zhengzhou University, Zhengzhou Henan 450001)
【Abstract】:The study of the influence of changes in small-world network parameters on the discharge characteristics of neural network will play an important role in promoting the research work of epilepsy and other neurological diseases. The seizures of neural diseases such as epilepsy are always accompanied by the synchronous discharge of neural networks. At present, the research of neural networks is mainly based on hierarchical networks, and its topological structure cannot simulate the real biological neural network. However, the small-world network has certain biological neural network characteristics. The simulation analysis of the small-world neural network can make the simulation results closer to the neural network discharge of real organisms. By constructing a small- world network, a small-world neural network was constructed based on the Izhikevich neuron model, short-term synaptic plasticity regulation mechanism and synaptic dynamics and is analyzed from the four aspects of the discharge pattern of excitatory neurons and inhibitory neurons, the discharge grid graph, the average discharge frequency and the overall discharge synchronization of the network.
【Key words】:Izhikevich neuron model;small world network;short-term synaptic plasticity;simulation analysis
0 引言
神经网络中所产生的同步性电生理活动是中枢神经 系统中普遍存在的一种现象,在神经网络的同步放电性 和人们的认知活动紧密相关 [1] 的同时,更多的证据也表 明异常的同步放电与癫痫 [2] 和老年痴呆症 [3] 等神经系 统疾病有关。因此,对神经元网络的仿真研究是了解神 经系统疾病发作的重要途经之一。
小世界网络是介于规则网络和随机网络之间的复杂 网络,大量研究表明,人类大脑具有短路径长度和高聚类系数的小世界网络特性 [4.5]。小世界网络近年来也成 为学术界的一个新兴研究热点。葛伟伦 [6] 对小世界网络 模型的静态特性进行了统计分析,张伟等 [7] 通过构建具 有突触可塑性的小世界网络从放电特性、突触权重动态 特性和复杂网络特性三个方面分析了小世界神经网络的 动态特性,周晶 [8] 进一步研究了一类具有随机长连接 强度的时滞小世界网络,最终给出了小世界网络连接强 度矩阵 D 的特征值分布。目前,在小世界网络特性方 面的研究较多,但是对以 Izhikevich 神经元 [9] 为节点的小世界网络的放电特性的研究较少。另外,研究小世 界神经网络中单个神经元的放电特性及其网络的同步放 电性将对癫痫等神经疾病的发作机理等方面的研究有一 定的理论意义。因此,本研究主要通过 MATLAB 软件 构建由 1000 个 Izhikevich 神经元组成的小世界神经网 络,在改变重连概率和突触连接数量的基础上对神经元 网络中兴奋性神经元和抑制性神经元放电情况的差异性 和神经元网络的同步放电情况等进行仿真分析。
1 神经元网络的构建
1.1 小世界网络的构建
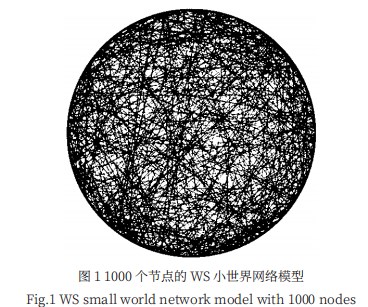
本研究采用 WS 小世界网络模型 [5] 构建节点数为 1000 的小世界网络,主要步骤与思路如下。
为了方便计算,首先用邻接矩阵 A 来表示网络,矩 阵 A 的每一个元素 Aij 表示节点 i 和节点j 是否相连;其 中, Aij=1 表示相连, Aij=0 表示不相连, i 为突触前神 经元, j 为突触后神经元。在这些条件的基础上构建一 个含有 1000 个节点的完全规则网络,每个节点与它最 临近的 k 个节点相连,之后以重连概率 P 进行随机边重 组,即可构成小世界网络。
其中, k 代表着神经元的突触连接数量,而对于概 率 P 的重连边而言, 需要将一个节点保持不变, 另一 个端点取为网络中随机的一个节点,但是这个随机的 节点不能是起点自身,也不能是与起点已经建立连接的 点。在 WS 小世界网络模型中, P=0 对应完全规则网络, P=1 则对应完全随机的网络,调节概率(0<
P<1) 可以 得到小世界网络拓扑,如图 1 所示。
为了刻画兴奋传递的单向性,我们将 Aij 中的 i 定义 为突触前神经元, j 定义为突触后神经元,并在小世界 网络构建完成后通过令 Aij=Aji=1 中随机一个取零的方式 实现。
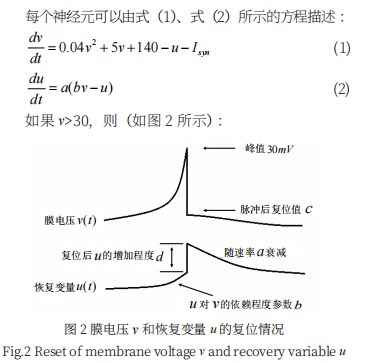
1.2 Izhikevich 神经元模型
HH 模型 [10] 过于复杂,不适合大规模仿真; 而 IF 模型 [11] 过于简单,脉冲发射模式过于单一。在 2003 年, Eugene M.Izhikevich 提出了 Izhikevich 模型 [9] , 在简化 HH 模型的同时具有大量的发射模式,更加接近 真实生物的脉冲放电特征且适用于大规模仿真。因此本 研究选取 Izhikevich 神经元模型作为神经元网络构建 的基本单位。
为了避免与快速尖峰活动相关的数值不稳定性,我 们使用了一阶欧拉法以 0.5 ms 的时间步长对每个神经 元的膜电压进行计算。
1.3 短期突触可塑性调节机制
本研究使用 Markram 等人的现象学模型 [12] 模拟 短期突触可塑性如式(3)、式(4)所示:
1.4 Izhikevich 神经网络的生成
依据神经解剖学实验结果,网络中兴奋性神经元和 抑制性神经元的比例为 4 ∶ 1[14] ,本研究构建的是含有 1000 个神经元的网络,由 800 个兴奋性神经元和 200 个抑制性神经元构成,网络中神经元之间的信息传递由 兴奋性突触和抑制性突触共同调节作用。在这样的基础 上构建一个含有 1000 个节点的小世界网络,它的每个 节点都对应于一个 Izhikevich 神经元,接着进行短期 突触可塑性和突触动力学的构建,最终生成小世界神经 网络。
2 神经元网络的仿真分析
本研究通过小世界神经网络的动态演化过程来探究 小世界网络参数的改变对神经元放电特性产生的影响。 分别从两类神经元的放电模式、放电栅图、平均放电频率和网络整体的放电同步性四个方面进行仿真分析。
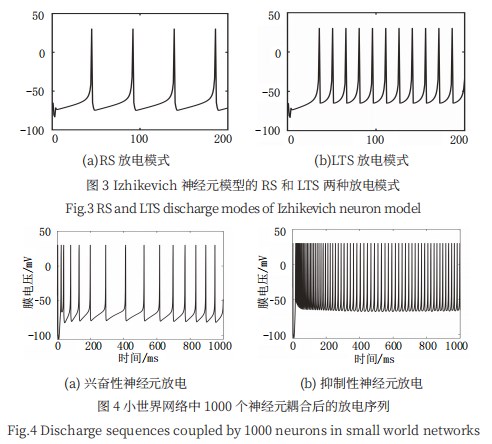
2.1 放电模式分析
在神经元总数为 1000.重连概率 P 为 0.5 且单个 神经元的突触连接数量 k 为 10 的小世界神经网络中随 机抽取的兴奋性神经元和抑制性神经元在 1000ms 内的 放电序列,如图 4 所示,其中,横坐标为仿真时间,纵 坐标为神经元的膜电压。我们发现,经过一段时间的调 控,兴奋性神经元和抑制性神经元的放电模式并没有发 生改变。
2.2 放电频率分析
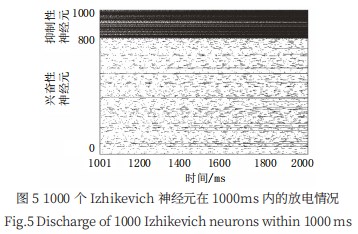
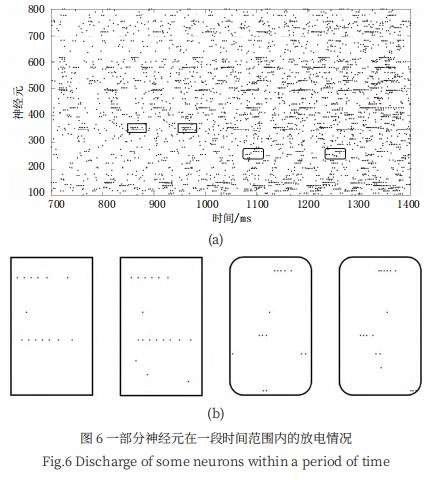
放电栅图可以反映神经元网络在时间域上的放电情 况,本研究在 2000ms 内对其进行了仿真,为了弱化网 络刚开始运行时所带有的随机性并减小实验误差,我们 取其后 1000ms 的放电情况做分析,如图 5 所示。其 中,横坐标为仿真时间,纵坐标代表放电的神经元序号。
在如图 6(a) 所示中,我们展示了模型中一小部分兴 奋性神经元在一段仿真时间内的放电情况。从如图 6(b) 所示的放大图中可以看出,在神经元放电序列中重复出 现了某些放电模式,并且这些神经元群的放电在固定的 时间间隔之后会可预见地发生,即它们发生的间隔时间 相对稳定,每个放电模式对应于一个神经元组的放电 激活,具有较强的突触连接和传导时间上的延迟,这与 Izhikevich 观察到的现象一致 [9]。
2.3 平均放电频率的分析
我们在保证单一变量的条件下分别改变重连概率 P 和单个神经元的突触连接数量 k,通过仿真来观察它们 的变化分别会对兴奋性神经元和抑制性神经元的平均放 电频率f产生怎样的影响,如式(11)所示。
2.3.1 重连概率 P
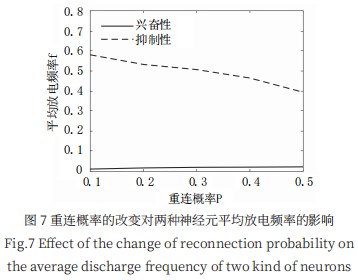
重连概率 P 决定了小世界网络中神经元连接的随机
性, P 越大代表着连接越随机。本研究通过改变小世界 网络的重连概率 P发现,重连概率 P 越大,兴奋性神经元的平均放电频率会逐渐增大,抑制性神经元的平均放 电频率会逐渐减小,并且抑制性神经元的平均放电频率 大于兴奋性神经元,如图 7 所示。
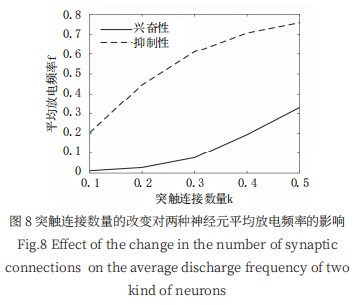
2.3.2 突触连接数量 k
通过改变小世界网络模型中的突触连接数量 k 可以 发现,随着突触连接数量 k 的增大,兴奋性神经元和抑 制性神经元的平均放电频率会逐渐增大,而抑制性神经 元的平均放电频率仍然大于兴奋性神经元,如图 8 所示。
2.4 神经元网络放电同步性测量
本研究采用计算神经网络的标准化互相关系数的方 法 [15] 对在不同的小世界网络参数下神经网络放电的同 步性进行分析。
接下来从重连概率 P 和突触连接数量 k 两个方面对 神经元网络放电的同步性进行分析。
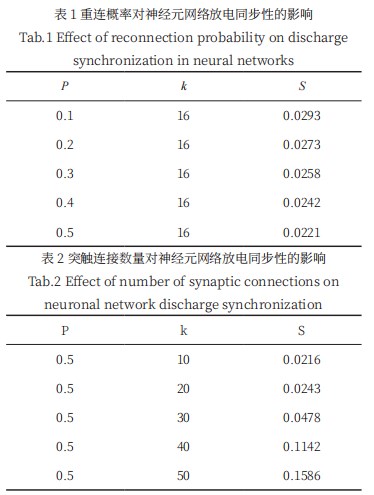
如表 1 所示, 网络整体的放电同步性也会随着重连 概率 P 的增大而减小;如表 2 所示,网络整体的放电同 步性也会随着突触连接数量 k 的增大而增大。
3 总结
本研究基于 WS 小世界网络模型,进而以 Izhikevich 神经元模型作为网络节点,通过短期突触可塑性和突触 动力学的构建,最终构建了小世界神经网络,进而探究 小世界网络参数的改变对神经网络放电特性的影响。分 别从两类神经元的放电模式、放电栅图、平均放电频率 和网络整体的放电同步性四个方面进行仿真分析,最终 发现:
(1)神经网络经过一段时间的调试后,兴奋性神经 元和抑制性神经元的放电模式并不会发生改变。
(2)对平均放电频率的仿真分析表明,小世界网络 的重连概率和突触连接数量的变化会对兴奋性神经元和 抑制性神经元的放电情况产生影响。突触连接数量不变 时,重连概率越大,兴奋性神经元的放电频率也会越大 而抑制性神经元的放电频率会逐渐减小;重连概率保持 不变时,突触连接数量越大,兴奋性神经元和抑制性神 经元的放电频率就会越大,但在这两种条件下,抑制性 神经元的放电频率均大于兴奋性神经元的放电频率。
(3)对神经元网络放电同步性的仿真分析表明,神 经元网络放电同步性与小世界网络中的重连概率和突触 连接数量之间有联系。重连概率越大,网络整体的放电 同步性将会越弱,而网络整体的放电同步性也会随着突 触连接数量的增大而增强。
参考文献
[1] CORREA Á,NOBRE A C.Spatial and Temporal Acuity of Visual Perception Can be Enhanced Selectively by Attentional set[J].Exp Brain Res,2008.189(3):339-344.
[2] NETOFF T I,SCHIFF S J . Decreased Neuronal Synchronization During Experimental Seizures[J] . Journal of Neuroscience,2002.22(16): 7297-7307.
[3] KÖNIG T,PRICHEP L,DIERKS T,et al .Decreased EEG Synchronization in Alzheimer's Disease and Mild Cognitive Impairment[J].Neurobiol,2005.26(2):165-171.
[4] ZALESKY A,FORNITO A,BULLMORE E.On the use of Correlation as a Measure of Network Connectivity[J]. Neuroimage,2012. 60(4):2096-2106.
[5] WATTS D J,STROGATZ S H .Collective Dynamics of 'Small-world' Networks[J].Nature,1998.393(6684):440-442.
[6] 葛伟伦,房丙午.小世界网络模型分析和算法模拟[J].通化师范 学院学报,2018.39(4):56-60.
[7] 张伟,郭磊,冉鹏飞,等.基于突触可塑性的小世界神经网络的 动态特性研究[J].生物医学工程学杂志,2018.35(4):509-517.
[8] 周晶 . 一类小世界网络的特征值研究[J] .现代信息科技, 2021.5(5):135-137.
[9] IZHIKEVICH E M,GALLY J A,EDELMAN G M .Spike- timing Dynamics of Neuronal Groups[J].Cerebral Cortex, 2004.14(8):933-944.
[10] HODGKIN A L,HUXLEY A F.A Quantitative Description of Membrane Current and its Application to Conduction and Excitation in Nerve[J].Bulletin Math Biol,1990.52(1): 25-71.
[11] ABBOTT L F.Lapicque's Introduction of the Integrate- and-fire Model Neuron (1907)[J].Brain Res Bull,1999.50(5-6): 303-304.
[12] MARKRAM H,WANG Y,TSODYKS M .Differential Signaling Via the Same Axon of Neocortical Pyramidal Neurons[J].Proc Natl Acad Sci USA,1998.95(9):5323-5328.
[13] GUPTA A,WANG Y,MARKRAM H.Organizing Principles for a Diversity of GABAergic Interneurons and Synapses in the Neocortex[J].Science,2000.287(5451):273-278.
[14] Izhikevich E M.Simple Model of Spiking Neurons[J]. IEEE Trans Neural Netw,2003.14(6):1569-1572.
[15] POUGET A,DAYAN P,ZEMEL R.Information Processing with Population Codes[J].Nat Rev Neurosci,2000.1(2): 125-132.
关注SCI论文创作发表,寻求SCI论文修改润色、SCI论文代发表等服务支撑,请锁定SCI论文网!
文章出自SCI论文网转载请注明出处:https://www.lunwensci.com/jisuanjilunwen/56058.html