SCI论文(www.lunwensci.com)
摘 要:RSA 算法作为应用较为广泛的非对称加密算法,经过蒙哥马利模乘等算法的优化后主要基于有限域运算中大数的 加法运算和乘法运算,数位规模通常在 1024 位甚至更高。大数的乘法运算随着参与运算位数的增加会导致 RSA 算法的运行时 间效率下降。随着多核处理器架构的普及,如何在多核多线程并行运算背景下提高 RSA 算法效率就成为解决 RSA 算法性能瓶 颈的关键。本文通过多核并行运算背景下分析大数乘法算法从而提出一种改进的适应多核运算的大数相乘算法,依靠此算法提 高 RSA 算法和大规模科学计算中高精度浮点数运算效率。
关键词:非对称加密算法,RSA,大数乘法运算,COMBA 算法
Design and Implementation of an Improved Multiplication of Large Prime Numbers
DA Simeng
(Ordos Human Resources and Social Security Bureau, Ordos Inner Mongolia 017400)
【Abstract】: As a widely used asymmetric encryption algorithm, the RSA algorithm is mainly based on the addition and multiplication of large numbers in finite field operations after the optimization of Montgomery modular multiplication and other algorithms. The digital scale is usually 1024 bits or even higher. The multiplication of large numbers will lead to a decrease in the running time efficiency of the RSA algorithm as the number of bits involved in the operation increases. With the popularization of multi-core processor architecture, how to improve the efficiency of RSA algorithm in the context of multi-core and multi-thread parallel computing has become the key to solving the performance bottleneck of RSA algorithm. This paper analyzes the multiplication algorithm of large numbers in the context of multi-core parallel computing, and proposes an improved multi-core multiplication algorithm for large numbers. Relying on this algorithm, it improves the efficiency of high-precision floating-point arithmetic in RSA algorithm and large-scale scientific computing.
【Key words】: asymmetric encryption algorithm;RSA;big integer multiplication;COMBA algorithm
0 引言
RSA 密码算法作为迄今最成熟最广泛应用的公钥密 码体制,由于其安全性高、抗数学攻击能力强等优点而 被广泛用于 SoC 智能芯片等各领域 [1]。
RSA 算法的安全性是基于数论和计算复杂性理论, 即计算两个大素数乘积是十分容易的,但是想要很快 将两个大素数的乘积分解,求出它的因子在计算上是 困难的,至今还没有一种方法能够很好地将其破解 [2]。 计算机科学领域近年来涌现出了很多关于 RSA 算法研 究, 包括了软件和硬件领域。作为 RSA 算法的提出人Rivest 提出了硬件思路, 而 Shamir and Adleman 则 提出了先进的模运算的算法 [3]。RSA 加密算法迄今为止 已经成功商业运营超过 40 年,由于计算性能和 RSA 算 法研究的深入进行,在 2001 年 Lenstra and Verheul 得 出结论表明如果想要在 2040 年仍然确保 RSA 算法的安 全性,就要将目前流行的 1024 位的秘钥扩大三倍 [4]。随 着多核多线程架构的诞生和普遍使用。由于 RSA 算法 的使用范围非常广泛,且很多项目并没有专门针对 RSA 算法的硬件加速器支持,因此本文聚焦在多核并行计算 背景下从纯软件角度提升 RSA 算法运行的时间性能。
RSA 算法的运行性能的关键点在于模幂运算即 C=Me mod n 和 M=Cd mod n。模幂运算通常会被分解 为一系列的模乘运算实现优化。许多现代密码学算法都 强烈依赖于对大整数的模运算,所需大整数通常是素数 或两个素数的乘积。因此提升 RSA 算法性能相关研究 的一个重点方向在于有限域中如何提升大数运算性能。 在模幂运算中通常有大概 25% 的运算时间用于乘法操 作 [5] ,因此近年来关于大数相乘算法的研究一直是 RSA 算法性能提升的重点。
提高加密算法效率的一种有效方式是在有限域中提高 大数乘法的效率 [6]。目前软件提高大整数乘法算法的研究 主要集中在两方面:(1)基于现有大数乘法运算较为成熟 的算法例如基线算法、Karatsuba 算法、Toom-Cook3 算法进行算法优化和性能调优;(2)随着多核多线程 CPU 的普及, 通过提高算法的并行度进而提升算法的 时间性能。本文结合上述两种研究思路,通过引入一种 更适应多核多线程运算规则的大数乘法算法,从而提高 整个 RSA 算法的运行时间效率。
1 大数相乘算法效率比较与改进的大数相乘算法
目前的处理器对于二进制数位的移位运算会比乘法 要快很多,因此可以使用左移位操作代替乘以 2 的次幂, 乘以不同数的乘法也可以用一连串的移位和加减法来代 替。大数相乘的算法主要有基线算法、傅立叶相乘算法、 Karatsuba 乘 法、Toom-Cook3 相 乘 算 法。Karatsuba 乘法和 Toom-Cook3 相乘算法的核心思路是一致的,只 不过在应用分治操作时 Karatsuba 乘法是分为两部分, 而 Toom-Cook3 相乘算法则是分为三部分。由于中国余 数定理使得 RSA 算法的操作数的规模减小了一半,因此 即使 4096 位的大数运算也可以减半位 2048 位,因此本 文基于上述原因对于所需位数十分庞大的傅立叶相乘不 做过度赘述。我们分别对多线程运行情况下在运算规模 被分解为较小位数的情况下对 Karatsuba 乘法、Toom- Cook3-way 相乘和基线相乘法进行性能分析并比较其 在 64 位、128 位、512 位、768 位、1024 位、1536 位、 2048 位等 7 种较常见情况下的理论复杂度和消耗时间 [6]。
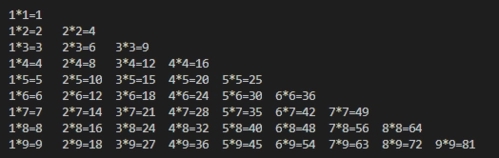
下面我们介绍 COMBA 算法,想要了解 COMBA 技 术首先来看一下两个大数相乘的过程。例如需要对 X 和 Y 两个 5 位的大数相乘,每一个大数位为 b 个二进制位。 其结果存放在目标数组 T 里面,则在构造 T[n] 的元素时 对其中所要存放的元素在得到两个相乘的大数的时候已经 可以确定了,并且它们之间满足如公式(1)所示的关系:
X0Yn-1+X1Yn-2+X2Yn-3 ……+Xn-1Y0=T[n-1] (1)
也就是说 T 的元素的位置也就是 n-1 等于上述公式里面的等式左边的 X 和 Y 的下标的和。因此就可以在 没有进行完整的大数相乘的时候,甚至是任何时候,得 到想得到的任何一个位置上的目标数组 T 的值,也就是 X×Y 的任何位置上的值(此时可以不考虑进位)。这就 是 COMBA 算法优势所在。下面通过 COMBA 算法的 大数相乘的伪代码进行比较来说明其效率明显提升的原 因,下面再看一下 COMBA 算法的伪代码。
我们看到在 CombaMul (a,d,T) 函数里, 和前面的 基线算法相比具有两个重大的优点。
(1) CombaMul 函数的运算过程是垂直式的运算, 在运算 T[i] 的时候可以利用公式(1)的等式来构造出 该列的值,也就是 T[i] 的值。同时由于 Temp 值可以 常驻 CPU 寄存器,因此可以降低内存访问次数。这在 乘法运算当中起着非常关键的作用。
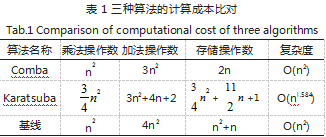
(2) 基线算法需要在每一次的 Temp 的计算结果 后进行一次 mod 操作取个位和位移操作取进位的过程, 也就是说在需要 k2 次的 mod 操作和位移操作,而在 CombaMul 函数中由于只是在每一列的结束的时候才 进行 mod 操作和位移操作,因此其次数只是需要 2k-1 次。从而提升了效率。如表 1 所示展示了基线算法、 Karatsuba 算法与 COMBA 算法在 n 位大数相乘时所 需乘法、加法、存储操作的次数。
2 性能测试与分析
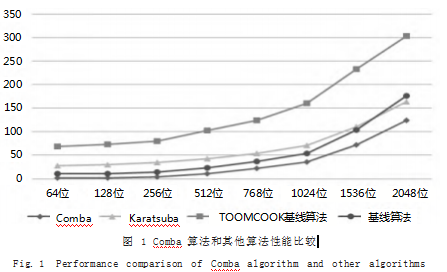
笔者基于英特尔酷睿 i7-10700F 处理器(8 核心 16线程, 主频 2.90GHz) 和 Win32 平台 MSVC 编译器环 境对上述程序 COMBA 大数相乘算法进行代码实现,并 与基线算法、Karatsuba 算法、TOMMCOOK-3 算法 在不同大数规模(分别为 64 位、128 位、512 位、768 位、1024 位、1536 位、2048 位) 下相乘结果进行了比 较,结果如图 1 所示(运算结果时间单位为毫秒,循环 次数为 10000 次)。
从图 1 中可以看出多核多线程背景下在 64 位到 2048 位大数相乘过程中 COMBA 算法始终保持着时间 效率的优势。其中在 64 位时比效率排名第二的基线算 法提高 88.6%,在 128 位时比效率排名第二的基线算 法提高 83.8%,在 256 位时比效率排名第二的基线算 法提高 70%,在 512 位时比效率排名第二的基线算法 提高 51.7%,在 768 位时比效率排名第二的基线算法 提高 41%,在 1024 位时比效率排名第二的基线算法提 高 33.7%,在 1536 位时比效率排名第二的基线算法提 高 30.6%, 在 2048 位时比效率排名第二的 Karatsuba 算法提高 24.2%。从上述数据可以看出随着相乘大数 规模的增加 COMBA 算法的比较优势也在下降,从 64 位大数运算中提高 88.6% 到 2048 位大数运算中提高 24.2%,随着大数位数的增加其算法优势呈线性降。
3 总结
本文设计的 COMBA 大数乘法运算算法通过采用不 进位的垂直式运算和降低内存访问次数的方法在大数乘
法中大大的减少了在多核多线程的纯软件环境下的耗时 且次数庞大的位移操作。本算法可以在无特殊硬件加速 器的情况下提高 RSA 算法中大数相乘运算的运行效率。 该算法将大数乘法运算的效率在 64 位大数运算中提高 了 88.6%,在 2048 位大数运算中提高了 24.2%。
参考文献
[1] 刘莺迎.基于余数系统抗MESD攻击的RSA算法[J].计算机 应用与软件,2021(4):324-327.
[2] 周金治,高磊.SSS基于多素数和参数替换的改进RSA算法研 究[J].计算机应用研究,2019.36(2):495-498.
[3] JOPPE W BOS,MARTIJN STAM.Computational Cryptography Algorithmic Aspects of Cryptology[M]. 2020:226-228.
[4] LENSTRA A K,VERHEUL E R.Selecting Cryptographic Key Sizes[J].Journal of Cryptology,2001.14(4):255-293. [5] DENIS T S,ROSE G.BigNum:math:Implementing Cryptographic Multiple Precision Arithmetic[M].2006: 91-92.
[6] KOVTUN V,OKHRIMENKO A.Approaches for the Performance Increasing of Software Implementation of Integer Multiplication in Prime Fields[J].IACR Cryptology Eprint Archive,2012.3(2):170-175.
关注SCI论文创作发表,寻求SCI论文修改润色、SCI论文代发表等服务支撑,请锁定SCI论文网!
文章出自SCI论文网转载请注明出处:https://www.lunwensci.com/jisuanjilunwen/54714.html